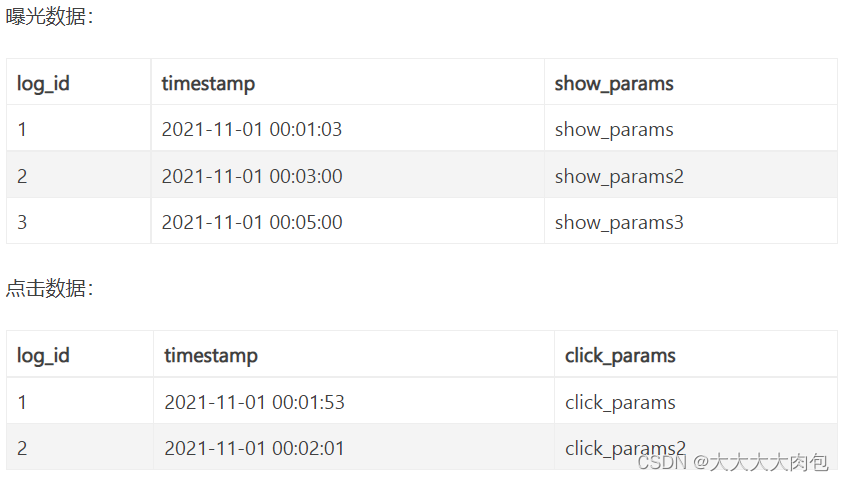
判断题:
- 如果一个NP完全问题能在多项式时间内得到解决,那么NP中的每一个问题都能在多项式时间内求解。(T)
- 可以用如下方法来证明某结论X成立:先假设X不成立,在此假设基础上推出X成立,则可以证明X成立。(T)
- 一个二倍近似算法得到的解总比一个四倍近似算法得到的解更好。(F)
- 问一个图是否存在大小为k的点覆盖,很容易证明该问题是NP问题;但是问一个图是否不存在一个大小为k的点覆盖,却很难证明该问题是否属于NP问题。(T)
计算题:

算法的定义和特征
1)什么是算法?
算法是求解某一特定问题的一组有穷规则,它是由若干条指令组成的有穷符号串。
2)算法的五个特性
确定性、可实现性、输入、输出、有穷性
3)算法设计的质量指标
正确性、可读性、健壮性、效率与存储量
算法与程序的区别
程序:一个计算机程序是对一个算法使用某种程序设计语言的具体实现。
任何一种程序设计语言都可以实现一个算法。
算法的有穷性意味着不是所有的计算机程序都是算法。
算法复杂性
算法复杂性 = 算法所需要的计算机资源 = 时间复杂性 + 空间复杂性
常见的多项式限界函数:
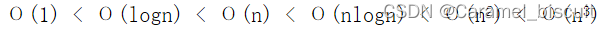
常见的指数时间限界函数:
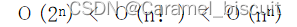
递归
直接或间接地调用自身的算法称为递归算法。
函数自身给出定义的函数称为递归函数。
基于归纳的递归——Fibonacci数列
无穷数列1,1,2,3,5,8,13, 21,34,55,…,称为Fibonacci数列。
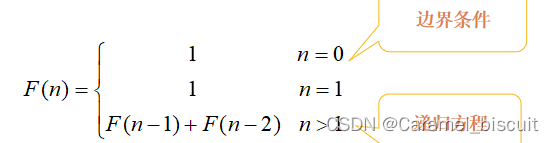
int fibonacci(int n)
{
if (n <= 1) return 1;
return fibonacci(n-1)+fibonacci(n-2);
}
分治算法总体思想
将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治法能解决的问题的特征:
- 该问题的规模缩小到一定的程序就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
- 子问题的解可以合并为原问题的解。
- 各个子问题是相互独立的。
分治法的基本步骤:
(1)分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题。
(2)解决:若子问题规模较小而容易被解决则直接解决,否则递归地解各个子问题。
(3)合并:将各个子问题的解合并为原问题的解。
分治法的复杂性分析
一个分治法将规模为n的问题分成k个规模为n/k的子问题。
则有:
f(n):表示将子问题合并为原问题的解。
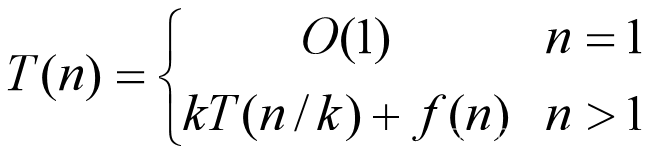
填空题


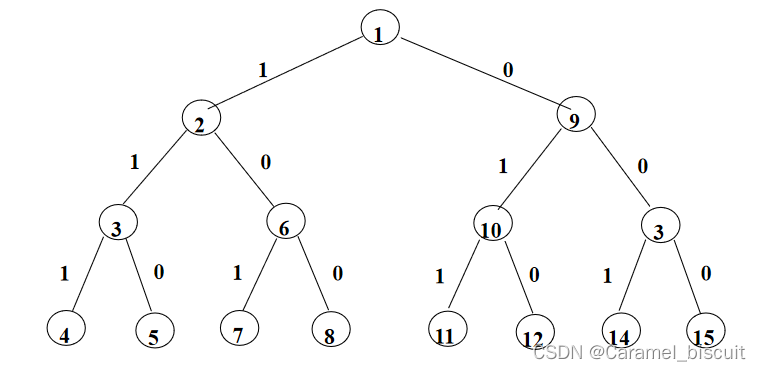
画出用回溯法求解n=3时,0-1背包问题的解空间树
当物品重量={20,15,10},价值为{20,30,25}时,背包容量为25时的搜索解空间树
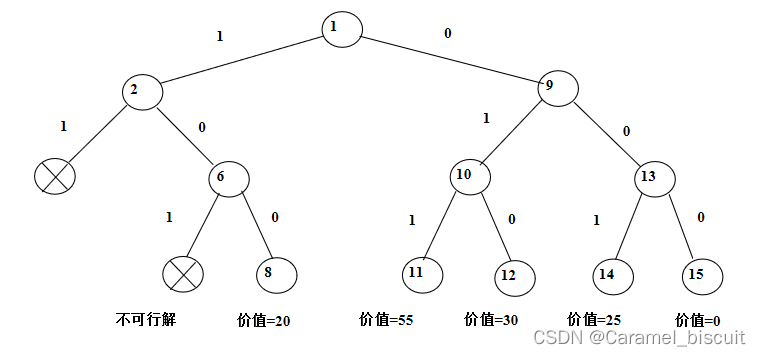
用分支限界法求解0-1背包问题
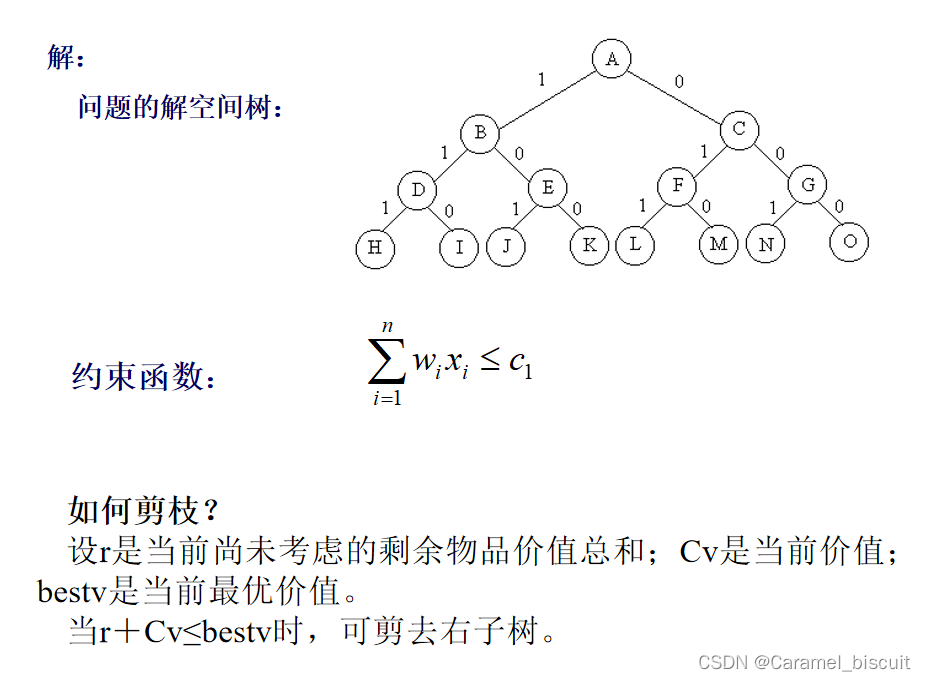
使用动态规划求解0-1背包问题
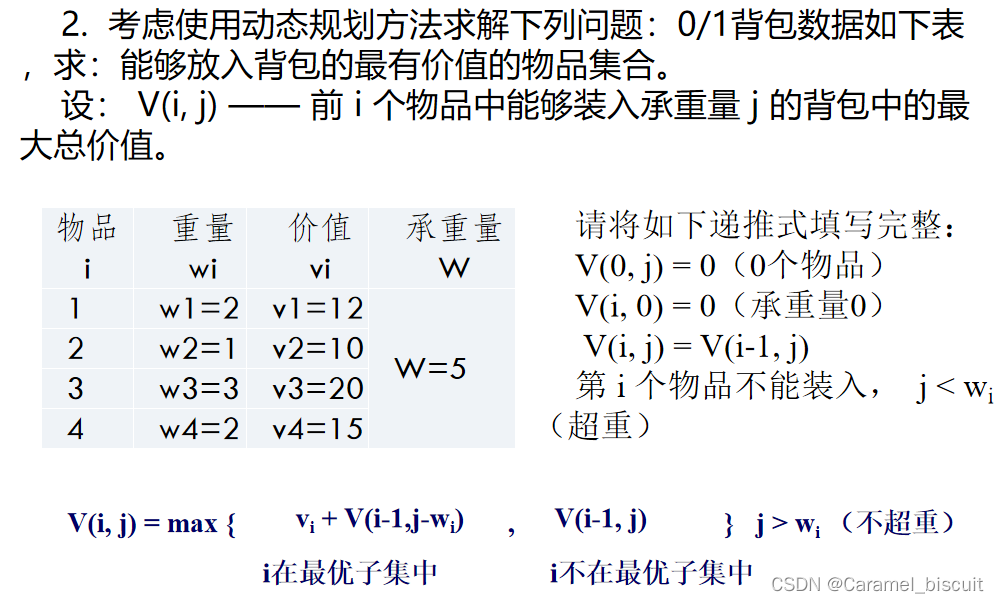
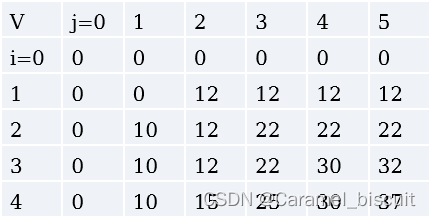
最少加油次数


用回溯法搜索子集树

用回溯法搜索排列树

合并排序