SOT23封装
三极管
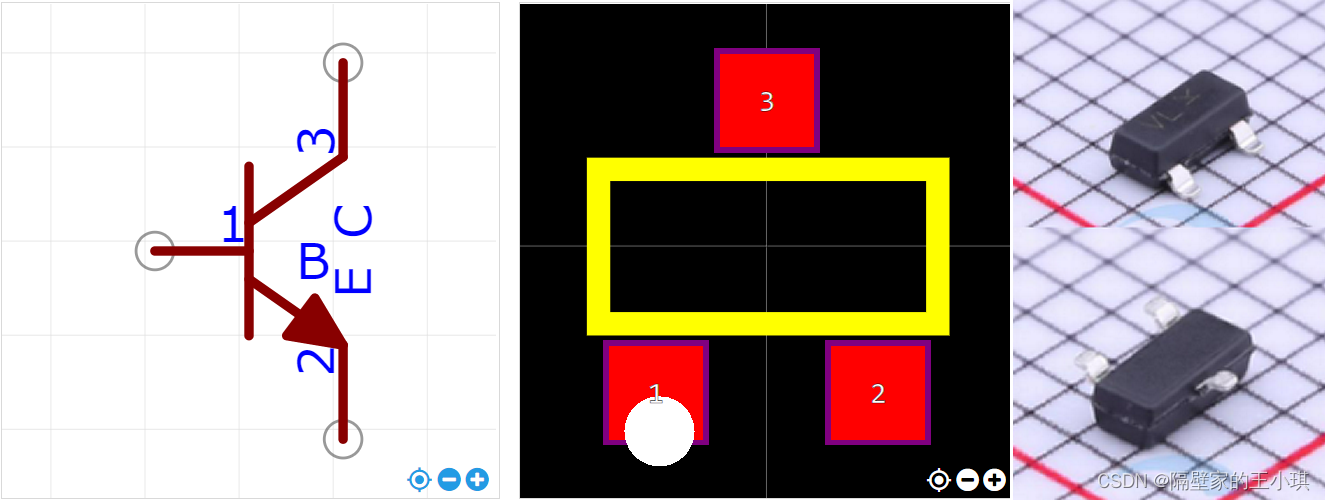
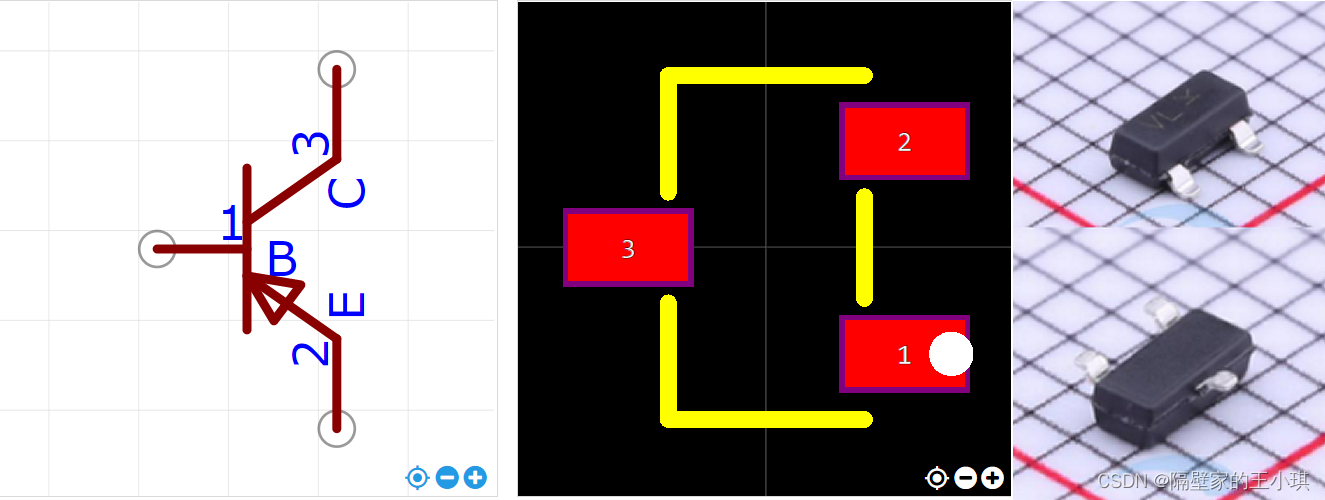
三极管为SOT23封装时,无论是NPN还是PNP。
引脚分布1脚为基极(B),2脚为发射极(E),3脚为集电极©。
 NPN NPN
|
 PNP PNP
|
MOS管
MOS管为SOT23封装时,无论是N-MOS还是P-MOS。
引脚分布1脚为栅极(G),2脚为源极(S),3脚为漏极(D)。
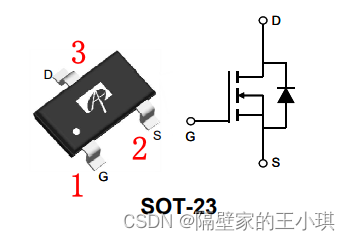 N-MOS N-MOS
|
 P-MOS P-MOS
|
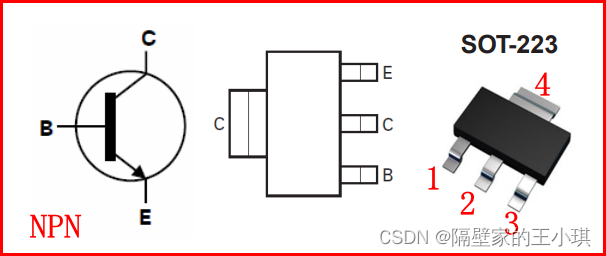
三极管
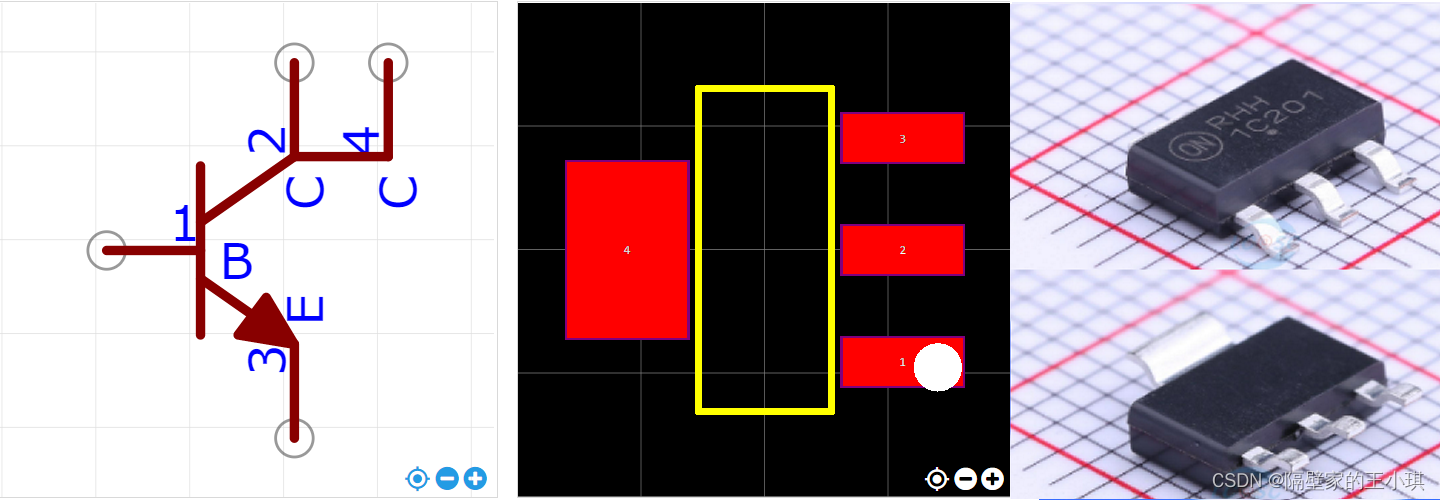
三极管为SOT223封装时,无论是NPN还是PNP。
引脚分布1脚为基极(B),2脚为发射极(E),3脚为集电极©。

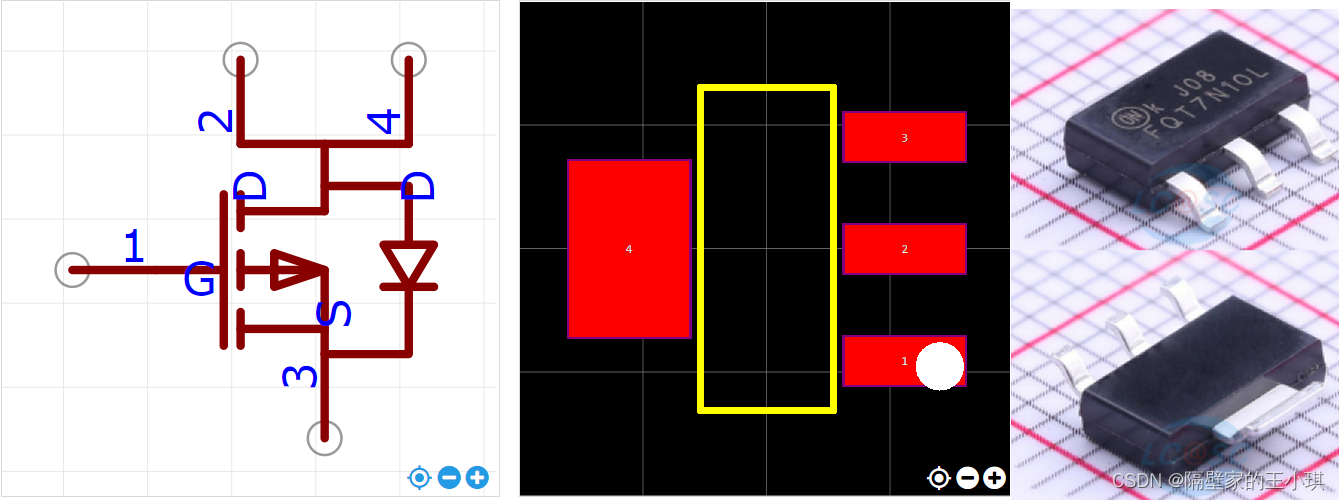
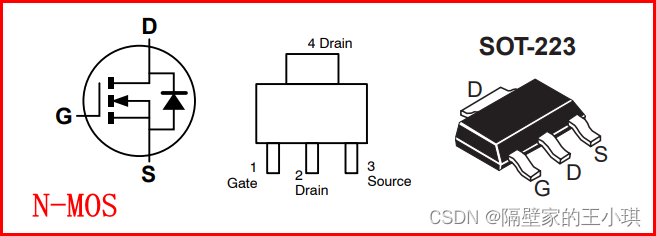
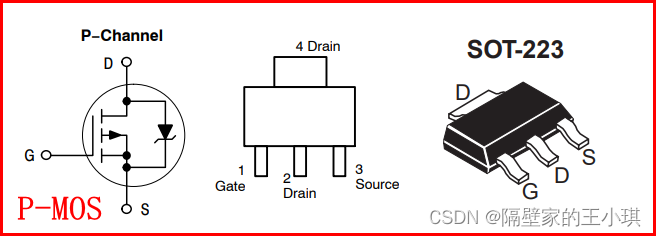
MOS管
MOS管为SOT223封装时,无论是N-MOS还是P-MOS。
引脚分布1脚为栅极,3脚为源极,2、4脚为漏极。有些封装2脚伸出可焊接,有些封装2脚悬空。
SOT23-PNP-原理图-PCB-实物图
SOT23-NMOS-原理图-PCB-实物图

SOT23-PMOS-原理图-PCB-实物图

SOT223-NPN-原理图-PCB-实物图
SOT223-PNP-原理图-PCB-实物图
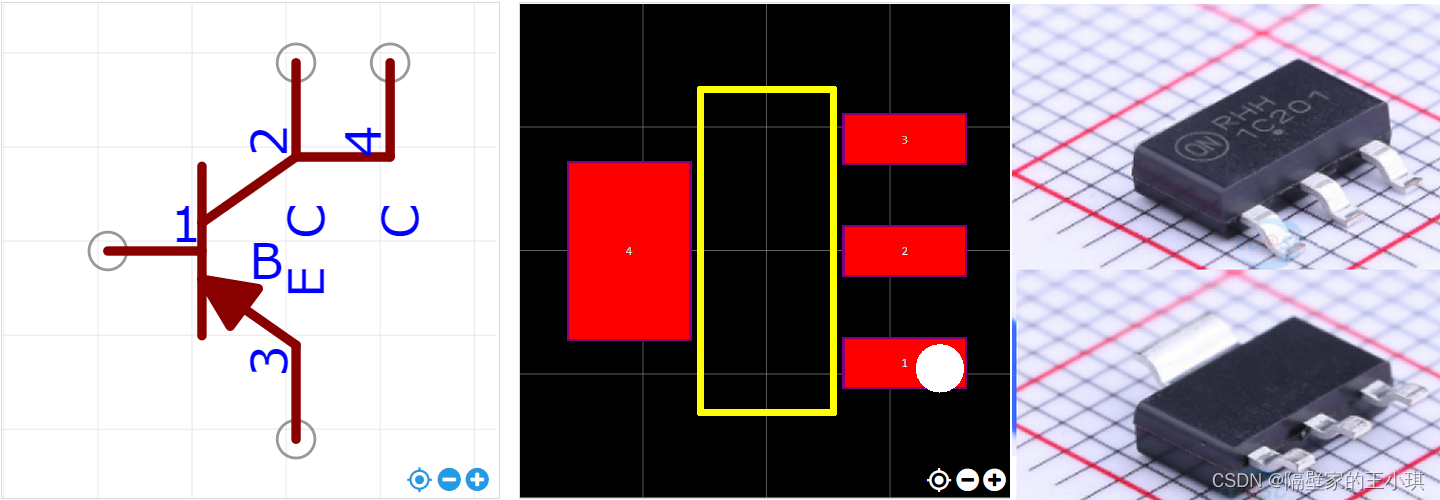
SOT223-NMOS-原理图-PCB-实物图

SOT223-PMOS-原理图-PCB-实物图