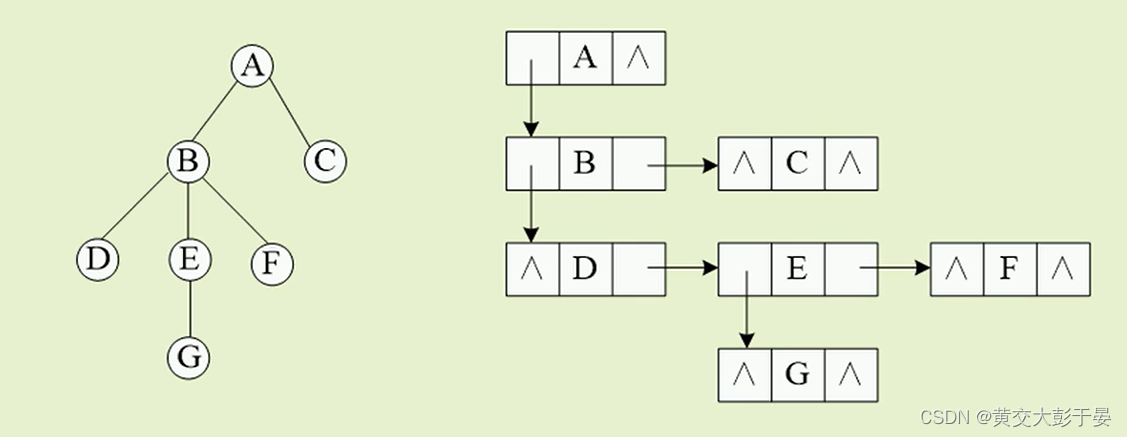
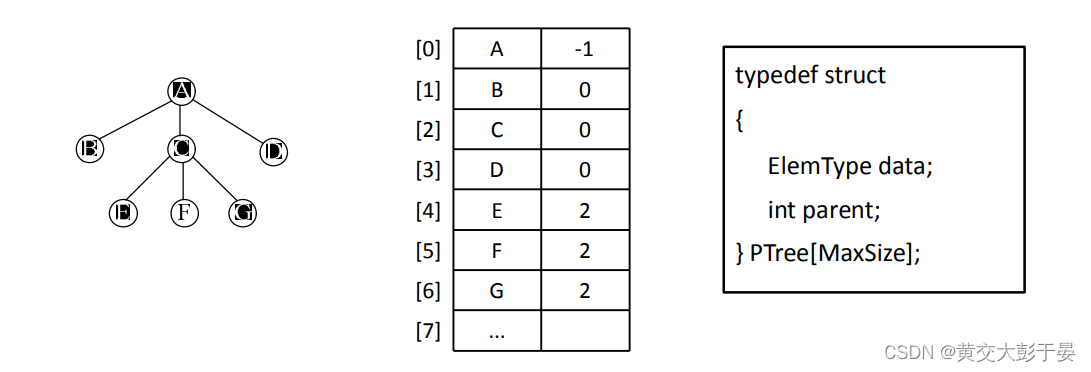
双亲存储结构
● 做法
• 一种顺序存储结构 , 用一组连续空间存储树的所有节点,
• 同时在每个节点中附设一个伪指针指示其双亲节点的位置
• 按顺序依次存储 , 逐层逐个节点存储在数组里面
● 定义存储结构
typedef struct { //定义数据区 ElemType data; //指向其双亲在数组中的位置 int parent; }PTree[MaxSize];
孩子链表存储结构
● 方法
• 存储每个节点的值 , 以及所有孩子的链接
• 按树的度 ( 即树中所有节点度的最大值 ) 设计节点的孩子节点指针域个数
• 从根节点起 , 逐个链接其子节点
● 结构定义
typedef struct node { //存储数据 ElemType data; //存储其孩子的指针数组 struct node *sons[MaxSons]; }TsonNode;// MaxSons 为最多的孩子节点个数
孩子兄弟链存储结构
● 方法
● 孩子兄弟链存储结构是为每个节点设计三个域
• 一个数据元素域
• 一个该节点的第一个孩子节点指针域
• 一个该节点的下一个兄弟节点指针域
因为每个节点可能有多个孩子 , 并且这几个孩子是兄弟 , 所以我们参考广义表的构建 , 把单个节点的孩子们 , 连成一个单链表 ,然后节点的其中一个 指针 *vp 指向 其第一个孩子 , 节点 的另一个指针 *hp 指向同级节点的兄弟
参考链接: http://t.csdn.cn/4yPjZ
注意 : 我们每一层 , 是根据一个节点的孩子进行构成单链表的
至于 ,如果同一层有两个节点, 并且这两个节点都有子树 , 我们就要对这两个结点的孩子分别设置子单链表
节点的数据结构定义:
typedef struct tnode { ||节点的值 ElemType data; || 指向兄弟 struct tnode *hp; || 指向孩子节点 struct tnode *vp; }TSBNode;
例: 以孩子-兄弟链作为存储结构 , 求树的高度
● 设 f(t)为树t的高度 , 有
{ 0 , t 为NULL
f(t)= { 1 , t 没有孩子节点
{ max {f(p)} + 1 , t 有其他孩子(p为t的孩子)
①当传入的树 ,是空的时候 , 我们没办法算高度 , 就返回 0
②当传入的树 ,只是一个节点的时候, 其没有孩子, 我们只返回 其本身高度 1
③当传入的树 , 其有孩子的时候 , 我们就需要先把其孩子当成树, 递归求出其孩子的高度 , 然后我们再在其孩子的高度基础上 ,加上根节点的高度 1
下面开始代码实操:
先传入树
int TreeHeigth(TSNode *t) {定义指向树节点的指针
TSNode *p;定义承载最大深度的变量max 和 中间变量 m
int m,max = 0;对上面三种情况进行判断
如果为空,返回 0
if(t==NULL) { return (0); }如果传入的树, 只有一个根节点 ,没有孩子, 我们就返回 1
else if(t->vp == NULL) { return (1); }剩下的一种情况 , 就是传入的树根 ,后面有孩子 , 我们就需要先算其孩子的高度
先把指针指向 树根的孩子
p = t -> vp;然后开始把其第一个孩子当成一个树, 求出其高度 , 然后 我们再把指针指向 孩子的兄弟 ,接着算出高度 , 让几个孩子的高度先存放在 m 中 , 最大的暂存在 max 中 , 当把所有孩子遍历完的时候 (p指向NULL), 我们就可以算出其孩子的最大高度 , 然后我们返回 max+ 1 即可
while(p!=NULL) { m = TreeHeight(p); if(max<m) { max = m; } p = p->hp; } return (max+1);
上面完整代码如下:
int TreeHeight(TSNode *t)
{
TSNode *p;
int m,max =0;
if(t==NULL)
{
return 0;
}
else if(t->vp == NULL)
{
return (1);
}
else
{
//求 t 的子树的高度m
p = t->vp;
while(p!=NULL)
{
m = TreeHeight(p);
if(max<m)
{
max = m;
}
//遍历兄弟
p = p->hp;
}
return (max+1);
}
}
关于实现的讨论
相比二叉树 , 我们这样构建树 , 和广义表类似 ,但没广义表通用 , 没二叉树实用 , 我们这样做 ,是为了后面学习二叉树打基础 , 融汇贯通 , 所以我们这里要理解树的递归思想 ,结合上节我们广义表的构建 ,相信大家会对递归 , 链式存储有更深的理解 .
下面把主要调试代码奉上:
框架代码:
typedef struct tnode { ElemType data; //节点的值 struct tnode *hp; //指向兄弟 struct tnode *vp; //指向孩子节点 }TSBNode; int TreeHeight(TSNode *t); void TreeCreate(TSNode *&t); void TreeDisp(TSNode *t); int main() { TSNode *tree; TreeCreate(tree); TreeDisp(tree); printf("Height:%d\n",TreeHeight(tree)); return 0; }我们此处只是构建上面的例子的树 ,仅供调试 , 理解:
#include <stdio.h> #include <malloc.h> typedef char ElemType; typedef struct tnode { ElemType data; //节点的值 struct tnode *hp; //指向兄弟 struct tnode *vp; //指向孩子节点 } TSBNode; int TreeHeight(TSBNode *t); void TreeCreate(TSBNode *&t); void TreeDisp(TSBNode *t); int TreeHeight(TSBNode *t) { TSBNode *p; int m, max = 0; if(t==NULL) return(0); else if(t->vp==NULL) return(1); else { //求t的子树的最大高度max p=t->vp; while(p!=NULL) { m=TreeHeight(p); if(max<m) max=m; p=p->hp; } return(max+1); } } int main() { TSBNode *tree; TreeCreate(tree); printf("Height: %d\n", TreeHeight(tree)); TreeDisp(tree); return 0; } void TreeCreate(TSBNode *&t) { //本例仅建造说明中特定的树,以支持演示 TSBNode *a, *b, *c, *d, *e, *f, *g; a = (TSBNode *)malloc(sizeof(TSBNode)); b = (TSBNode *)malloc(sizeof(TSBNode)); c = (TSBNode *)malloc(sizeof(TSBNode)); d = (TSBNode *)malloc(sizeof(TSBNode)); e = (TSBNode *)malloc(sizeof(TSBNode)); f = (TSBNode *)malloc(sizeof(TSBNode)); g = (TSBNode *)malloc(sizeof(TSBNode)); a->data = 'a'; b->data = 'b'; c->data = 'c'; d->data = 'd'; e->data = 'e'; f->data = 'f'; g->data = 'g'; a->vp = b; a->hp = NULL; b->vp = d; b->hp = c; c->vp = NULL; c->hp = NULL; d->vp = NULL; d->hp = e; e->vp = g; e->hp = f; f->vp = NULL; f->hp = NULL; g->vp = NULL; g->hp = NULL; t=a; //a作为根 return; } void TreeDisp(TSBNode *t) { if(t!=NULL) { printf("node value: %c\n", t->data); printf("%c\'s first child --> ", t->data); TreeDisp(t->hp); printf("%c\'s brother(its father\'s another child) --> ", t->data); TreeDisp(t->vp); } else { printf("NULL\n"); } }
结尾 : 感谢 贺利坚老师 的b站课程 .