文章目录
- 基本介绍:
- 坐标系变换运算规则:
- 关系运算说明:
- 坐标系运算规则一:
- 坐标系运算规则二:
- 齐次坐标系:
- 齐次坐标系下的坐标变换:
- 眼在手外:
- 眼在手内:
- 解方程:
- - Tais方法
- 使用opencv完成手眼标定
- 欧拉角变换为旋转矩阵:
- 旋转矩阵变成欧拉角:
- 易错点:
基本介绍:
-
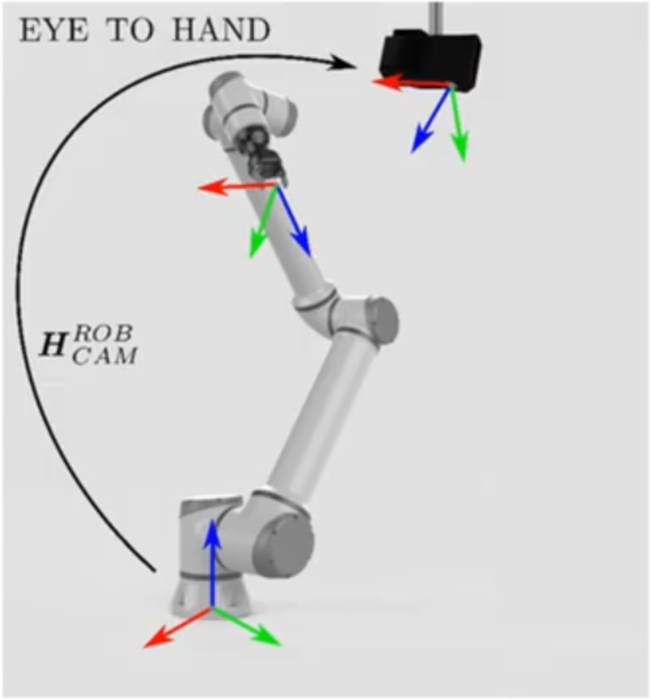
眼在手外(eye to hand):
相机固定在机械臂以外的地方,主要标定相机和基底坐标系的转换矩阵。
-
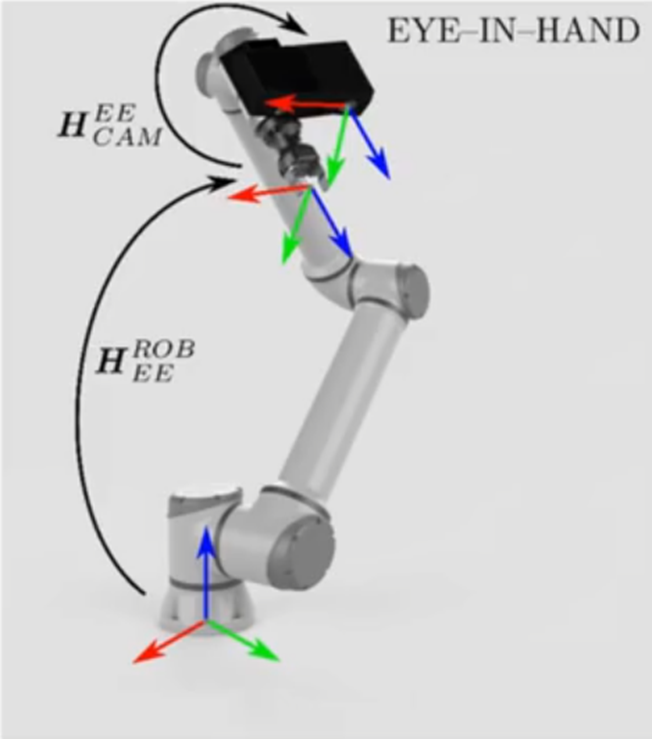
眼在手上(eye in hand):
相机固定在机械臂末端,主要标定相机和机械臂末端的转换矩阵。
坐标系变换运算规则:
e n d b a s e R _{end}^{base}R endbaseR:机械臂末端坐标系到机械臂基底坐标系的旋转矩阵
e n d b a s e T _{end}^{base}T endbaseT:机械臂末端坐标系到机械臂基底坐标系的平移矩阵
e n d b a s e M = [ e n d b a s e R e n d b a s e T 0 1 ] _{end}^{base}M = \begin{bmatrix} _{end}^{base}R & _{end}^{base}T \\ 0 & 1 \end{bmatrix} endbaseM=[endbaseR0endbaseT1]:机械臂末端坐标系到机械臂基底坐标系变换矩阵
以上等价于:机械臂末端坐标系在基底坐标系下的描述
关系运算说明:
e
n
d
b
a
s
e
R
=
b
a
s
e
e
n
d
R
−
1
e
n
d
b
a
s
e
M
=
b
a
s
e
e
n
d
M
−
1
e
n
d
b
a
s
e
T
=
{
=
−
b
a
s
e
e
n
d
T
i
f
e
n
d
b
a
s
e
R
=
b
a
s
e
e
n
d
R
=
I
≠
−
b
a
s
e
e
n
d
T
i
f
e
n
d
b
a
s
e
R
≠
b
a
s
e
e
n
d
R
≠
I
_{end}^{base}R = ^{end}_{base}R^{-1} \\ _{end}^{base}M = ^{end}_{base}M^{-1} \\ _{end}^{base}T=\left\{ \begin{aligned} = & -^{end}_{base}T\quad if \quad_{end}^{base}R = ^{end}_{base}R = I \\ \neq & -^{end}_{base}T\quad if \quad _{end}^{base}R \neq ^{end}_{base}R \neq I \end{aligned} \right.
endbaseR=baseendR−1endbaseM=baseendM−1endbaseT={==−baseendTifendbaseR=baseendR=I−baseendTifendbaseR=baseendR=I
由于R是正交矩阵,正交矩阵的逆=正交矩阵的转置,所以有时候也会写为
e
n
d
b
a
s
e
R
=
b
a
s
e
e
n
d
R
T
^{base}_{end}R = ^{end}_{base}R^T
endbaseR=baseendRT
坐标系运算规则一:
假设有两个坐标系A,B,其中坐标系B中的点b是由坐标系A中的点a转换来的,则点a和点b之间有如下等式
a
=
B
A
R
∗
b
+
B
A
T
b
=
A
B
R
∗
a
+
A
B
T
a = {^A_B}R * b + {^A_B}T \\ b = {^B_A}R * a + {^B_A}T
a=BAR∗b+BATb=ABR∗a+ABT
由以上等式可以看出:
a
=
A
B
R
−
1
(
b
−
A
B
T
)
=
A
B
R
−
1
b
−
A
B
R
−
1
A
B
T
=
A
B
R
−
1
b
+
B
A
T
B
A
T
=
−
A
B
R
−
1
A
B
T
a = {^B_A}R^{-1}(b-{^B_A}T) \\ \quad\quad\;\,= {^B_A}R^{-1}b-{^B_A}R^{-1}{^B_A}T\\ \,= {^B_A}R^{-1}b+{^A_B}T \\ {^A_B}T = -{^B_A}R^{-1}{^B_A}T
a=ABR−1(b−ABT)=ABR−1b−ABR−1ABT=ABR−1b+BATBAT=−ABR−1ABT
坐标系运算规则二:
假设由三个坐标系A,B,C,已知如下关系: B A R , B A T , C B R , C B T {^A_B}R,{^A_B}T,{^B_C}R,{^B_C}T BAR,BAT,CBR,CBT,求 C A R , C A T {^A_C}R,{^A_C}T CAR,CAT
对于旋转矩阵 R R R: C A R = B A R ∗ C B R {^A_C}R = {^A_B}R*{^B_C}R CAR=BAR∗CBR
对于平移矩阵 T T T: C A T = B A T + B A R C B T {^A_C}T = {^A_B}T+{^A_B}R\;{^B_C}T CAT=BAT+BARCBT 形式麻烦!
齐次坐标系:
- 已知坐标系A下的点 a = ( x a , y a , z a ) T a = (x_a,y_a,z_a)^T a=(xa,ya,za)T,则点 a a a的齐次坐标系可以写成 a = ( x a , y a , z a , 1 ) T a = (x_a,y_a,z_a,1)^T a=(xa,ya,za,1)T
- 已知齐次坐标系下一点 p = ( a , b , c , d ) T p = (a,b,c,d)^T p=(a,b,c,d)T,则点 p p p的真实三维坐标为 p = ( a d , b d , c d ) T p = (\frac ad,\frac bd,\frac cd)^T p=(da,db,dc)T
- 齐次坐标系下的变换矩阵: B A M = [ B A R B A T 0 1 ] {^A_B}M = \begin{bmatrix} {^A_B}R & {^A_B}T \\ 0 & 1 \end{bmatrix} BAM=[BAR0BAT1]
- B A M = A B M − 1 {^A_B}M = {^B_A}M^{-1} BAM=ABM−1
齐次坐标系下的坐标变换:
- 已知a,b,c分别为坐标系A,B,C下的齐次坐标,则有如下关系:
a = B A M ∗ b b = C B M ∗ c a = B A M ∗ C B M ∗ c a = {^A_B}M * b\\ b = {^B_C}M * c\\ a = {^A_B}M * {^B_C}M *c a=BAM∗bb=CBM∗ca=BAM∗CBM∗c
眼在手外:
求解目标:机械臂基底坐标系到相机坐标系的变换矩阵 b a s e c a m e r a M ^{camera}_{base}M basecameraM
手眼标定坐标系表示:
- 机械臂基底坐标系 – base
- 机械臂末端坐标系 – end
- 相机坐标系 – camera
- 标定板坐标系 – board
实现方法:
- 把标定板固定在机械臂末端
- 使用相机拍摄不同机械臂姿态下的标定板图片n张,n>3
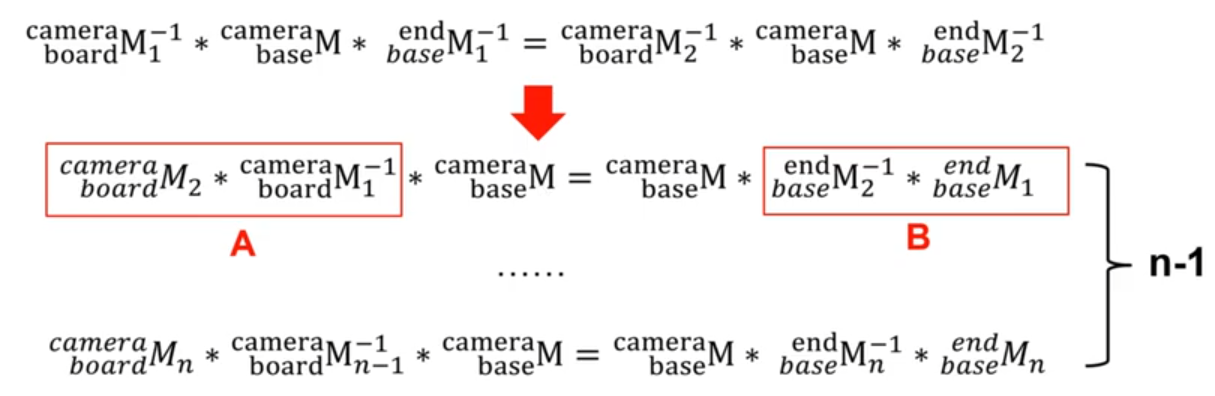
则对每张图片可知: b a s e c a m e r a M = b o a r d c a m e r a M ∗ e n d b o a r d M ∗ b a s e e n d M ^{camera}_{base}M = \;^{camera}_{board}M * \; ^{board}_{end}M * \;^{end}_{base}M basecameraM=boardcameraM∗endboardM∗baseendM
变形得:
e n d b o a r d M = b o a r d c a m e r a M − 1 ∗ b a s e c a m e r a M ∗ b a s e e n d M − 1 ^{board}_{end}M = \;^{camera}_{board}M^{-1} * \;^{camera}_{base}M * \;^{end}_{base}M^{-1} endboardM=boardcameraM−1∗basecameraM∗baseendM−1
其中:
b o a r d c a m e r a M : ^{camera}_{board}M: boardcameraM: 可由通过拍摄的标定板图片直接求解
b a s e e n d M : ^{end}_{base}M: baseendM: 可由机械臂末端位姿参数求得
e n d b o a r d M : ^{board}_{end}M: endboardM: 未知量,由于标定板固定在机械臂末端,所以对每组图片,该转换矩阵都相同
已知对每张图片:
e
n
d
b
o
a
r
d
M
=
b
o
a
r
d
c
a
m
e
r
a
M
−
1
∗
b
a
s
e
c
a
m
e
r
a
M
∗
b
a
s
e
e
n
d
M
−
1
^{board}_{end}M = \;^{camera}_{board}M^{-1} * \;^{camera}_{base}M * \;^{end}_{base}M^{-1}
endboardM=boardcameraM−1∗basecameraM∗baseendM−1
**则可以得到如下等式:**左乘
b
o
a
r
d
c
a
m
e
r
a
M
2
^{camera}_{board}M_2
boardcameraM2 右乘
b
a
s
e
e
n
d
M
1
^{end}_{base}M_1
baseendM1
眼在手内:
求解目标:机械臂末端坐标系到相机坐标系的变换矩阵 e n d c a m e r a M ^{camera}_{end}M endcameraM
手眼标定坐标系表示:
- 机械臂基底坐标系 – base
- 机械臂末端坐标系 – end
- 相机坐标系 – camera
- 标定板坐标系 – board
实现方法:
- 把标定板放在固定位置不动
- 移动机械臂末端,从不同角度拍摄n张标定板图片
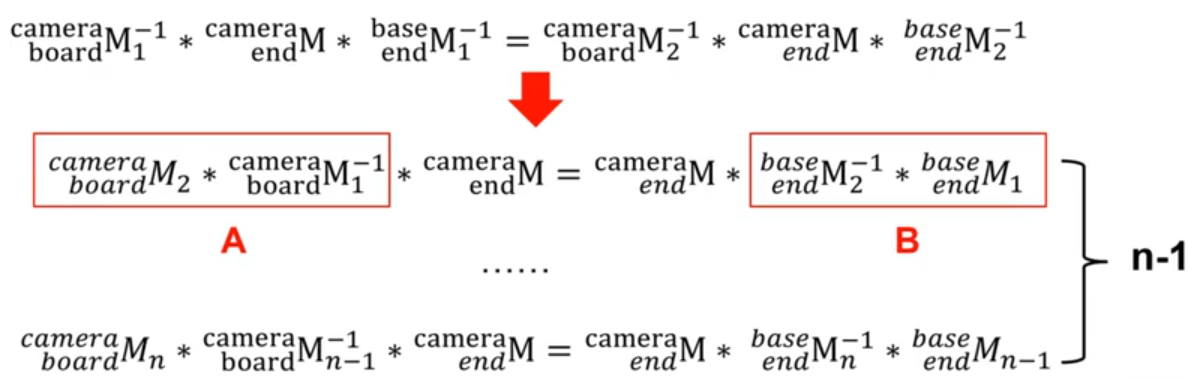
则对每张图片可知: e n d c a m e r a M = b o a r d c a m e r a M ∗ b a s e b o a r d M ∗ e n d b a s e M ^{camera}_{end}M = \;^{camera}_{board}M * \; ^{board}_{base}M * \;^{base}_{end}M endcameraM=boardcameraM∗baseboardM∗endbaseM
变形得:
b a s e b o a r d M = b o a r d c a m e r a M − 1 ∗ e n d c a m e r a M ∗ e n d b a s e M − 1 ^{board}_{base}M = \;^{camera}_{board}M^{-1} * \;^{camera}_{end}M * \;^{base}_{end}M^{-1} baseboardM=boardcameraM−1∗endcameraM∗endbaseM−1
其中:
b o a r d c a m e r a M : ^{camera}_{board}M: boardcameraM: 可由通过拍摄的标定板图片直接求解
b a s e e n d M : ^{end}_{base}M: baseendM: 可由机械臂末端位姿参数求得
b a s e b o a r d M : ^{board}_{base}M: baseboardM: 未知量,由于标定板全程固定在一个位置不动,所以对每组图片,该转换矩阵都相同
已知对每张图片:
b
a
s
e
b
o
a
r
d
M
=
b
o
a
r
d
c
a
m
e
r
a
M
−
1
∗
e
n
d
c
a
m
e
r
a
M
∗
e
n
d
b
a
s
e
M
−
1
^{board}_{base}M = \;^{camera}_{board}M^{-1} * \;^{camera}_{end}M * \;^{base}_{end}M^{-1}
baseboardM=boardcameraM−1∗endcameraM∗endbaseM−1
**则可以得到如下等式:**左乘
b
o
a
r
d
c
a
m
e
r
a
M
2
^{camera}_{board}M_2
boardcameraM2 右乘
e
n
d
b
a
s
e
M
1
^{base}_{end}M_1
endbaseM1
解方程:
无论是眼在手外还是眼在手内,都可以得到一个经典的方程组 A X = X B AX=XB AX=XB,这个方程组有n-1个方程 (n是拍摄的图片数量)
其中X是我们要求得的手眼矩阵,里面有6个线性无关的变量,其中旋转3个自由度,平移3个自由度。
- Tais方法
**形式变换:**由于A,B,X均为变换矩阵
A
=
[
R
A
T
A
0
1
]
B
=
[
R
B
T
B
0
1
]
X
=
[
R
X
T
X
0
1
]
A = \begin{bmatrix} R_A & T_A \\ 0 & 1 \end{bmatrix} \qquad B = \begin{bmatrix} R_B & T_B \\ 0 & 1 \end{bmatrix} \qquad X = \begin{bmatrix} R_X & T_X \\ 0 & 1 \end{bmatrix}
A=[RA0TA1]B=[RB0TB1]X=[RX0TX1]
则
A
X
=
X
B
AX=XB
AX=XB可以拆解成如下两个等式
{
R
A
R
X
=
R
X
R
B
(
R
A
−
1
)
T
X
=
R
X
T
B
−
T
A
\left\{ \begin{aligned} R_AR_X & =R_XR_B \\ (R_A-1)T_X & =R_XT_B-T_A \\ \end{aligned} \right.
{RARX(RA−1)TX=RXRB=RXTB−TA
Tais方法:先求解Rx,再求解Tx
旋转的表示:
**旋转矩阵:**3*3矩阵 R = R z R y R x R = R_zR_yR_x R=RzRyRx
旋转向量: r = ( x y z ) θ = n o r m ( r ) r = (x\;y\;z) \quad \theta = norm(r) r=(xyz)θ=norm(r)
刚体绕旋转轴旋转, r r r表示的是旋转轴的方向, r r r的长度表示刚体绕旋转轴的角度
旋转角: θ = ( θ x θ y θ z ) \theta = (\theta_x \; \theta_y \; \theta_z) θ=(θxθyθz)
旋转角又称欧拉角,一般情况下旋转角指的是坐标系绕x轴旋转后,再绕y轴旋转后,再绕z轴旋转分别的角度
使用opencv完成手眼标定


欧拉角变换为旋转矩阵:
R x ( θ x ) = [ 1 0 0 0 c o s θ x − s i n θ x 0 s i n θ x c o s θ x ] R y ( θ y ) = [ c o s θ y 0 s i n θ y 0 1 0 − s i n θ y 0 c o s θ y ] R z ( θ z ) = [ c o s θ z − s i n θ z 0 s i n θ z c o s θ z 0 0 0 1 ] R = R z R y R x R_x(\theta_x) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\theta_x & -sin\theta_x \\ 0 & sin\theta_x & cos\theta_x\end{bmatrix} \\R_y(\theta_y) = \begin{bmatrix} cos\theta_y & 0 & sin\theta_y \\ 0 & 1 & 0 \\ -sin\theta_y & 0 & cos\theta_y\end{bmatrix} \\ R_z(\theta_z) = \begin{bmatrix} cos\theta_z & -sin\theta_z & 0 \\ sin\theta_z & cos\theta_z & 0 \\ 0 & 0 & 1\end{bmatrix}\\R = R_zR_yR_x Rx(θx)=⎣⎡1000cosθxsinθx0−sinθxcosθx⎦⎤Ry(θy)=⎣⎡cosθy0−sinθy010sinθy0cosθy⎦⎤Rz(θz)=⎣⎡cosθzsinθz0−sinθzcosθz0001⎦⎤R=RzRyRx
旋转矩阵变成欧拉角:
R = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33}\end{bmatrix} R=⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤
θ Z = a t a n 2 ( r 21 , r 11 ) θ Y = a t a n 2 ( − r 31 , r 31 2 + r 33 2 ) θ X = a t a n 2 ( r 32 , r 33 ) \theta_Z = atan2(r_{21},r_{11}) \\ \theta_Y = atan2(-r_{31},\sqrt{r^2_{31}+r^2_{33}}) \\ \theta_X = atan2(r_{32},r_{33}) θZ=atan2(r21,r11)θY=atan2(−r31,r312+r332)θX=atan2(r32,r33)
solvePnP()
bool cv::solvePnP(InputArray objectPoints,
InputArray imagePoints,
InputArray cameraMatrix, // 相机内参
InputArray distCoeffs, // 相机畸变系数
OutputArray rvec, // R
OutputArray objectPoints, // T
bool useExtrinsicGuess = false,
int flags = SOLVEPNP_ITERATIVE)
易错点:
1. 利用calibrateCamera函数中计算的R、T,来作为标定板坐标系到相机坐标系的输入
问题分析:对手眼标定来说,这个R、T没有问题。但是由于后续的抓取来说,使用的物体三维坐标是相机重建的点云,即相机之前标定的内参下的点云。此时手眼标定的相机坐标系和实际抓取使用的相机坐标系轻微的不一致,导致抓取总是有轻微误差。
2. 识别标定板角点方向反了!
由于在建立棋盘格上的三维坐标系的时候,我们默认是从棋盘格左上角到右下角建立的,如果识别反了,则会有个别图片棋盘格识别的角点和输入的棋盘格三维坐标对应不上!

本篇为观看b站视频的笔记
在此附上原视频地址:
手眼标定–原理与实战