文章目录
- 非对称加密是什么
- 非对称加密通信流程
- RSA非对称加密算法
- 非对称加密工具类Util及案例演示
之前写过一篇关于DES对称加密的帖子,感兴趣的小伙伴可以去看看:DES对称加密算法
今天主要聊聊什么是非对称加密,以及它是如何实现的。
一、非对称加密是什么?
非对称加密(asymmetric cryptography),也称为公开密钥加密(Public-key cryptography),是密码学的一种算法,它需要两个密钥,一个是公开密钥,另一个是私有密钥。顾名思义,公钥可以任意对外发布;而私钥必须由用户自行严格秘密保管,绝不透过任何途径向任何人提供,也不会透露给要通信的另一方,即使他被信任。
非对称加密的重要性质:
1.加密的双向性
加密具有双向性,即公钥和私钥中的任一个均可用作加密,此时另一个则用作解密。
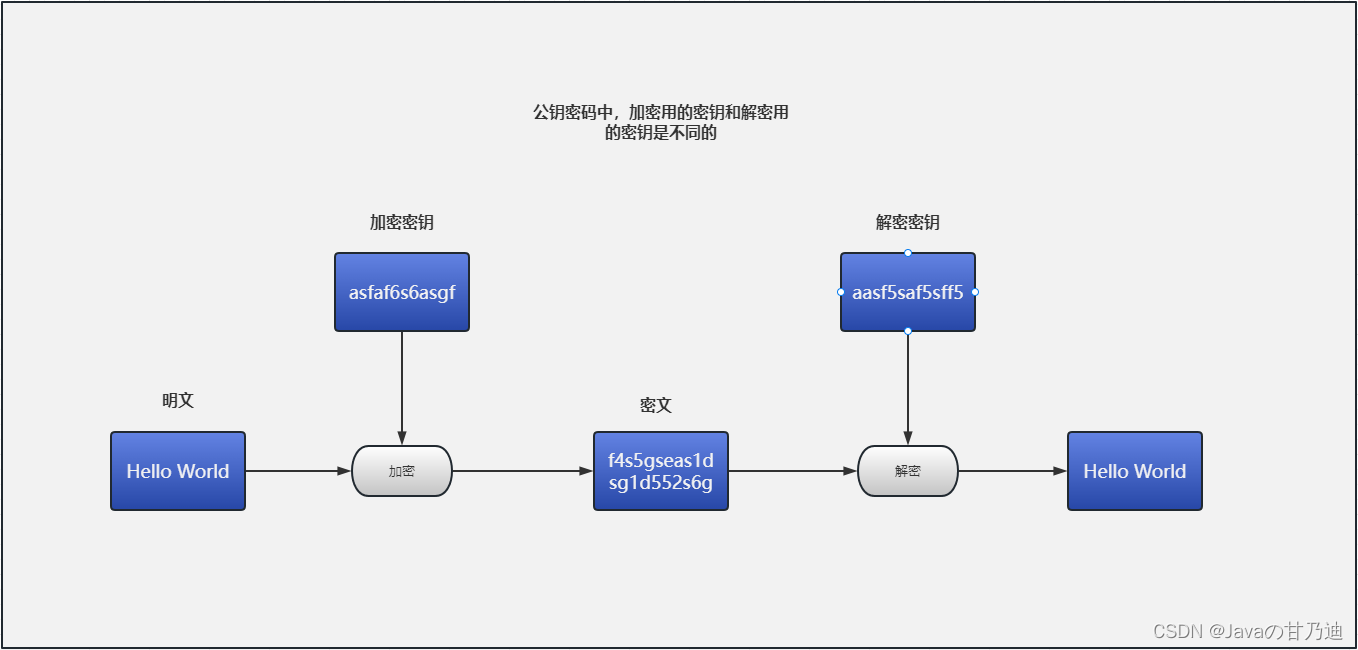
使用其中一个密钥把明文加密后所得的密文,只能用相对应的另一个密钥才能解密得到原本的明文,甚至连最初用来加密的密钥也不能用作解密,这是非对称加密最重要的性质或者说特点。
2.公钥无法推导出私钥
必须确保使用公钥无法推导出私钥,至少妄想使用公钥推导私钥必须在计算上是不可行的,否则安全性将不复存在。
虽然两个密钥在数学上相关,但如果知道了公钥,并不能凭此计算出私钥;因此公钥可以公开,任意向外发布;而私钥不公开,绝不通过任何途径向任何人提供。
在对称密码中,由于加密和解密的密钥是相同的,因此必须向接收者配送密钥。用于解密的密钥必须被配送给接收者,这一问题称为密钥配送问题。如果使用非对称加密,则无需向接收者配送用于解密的密钥,这样就解决了密钥配送的问题。
非对称加密中,密钥分为加密密钥和解密密钥两种。发送者用加密密钥对消息进行加密,接收者用解密密钥对密文进行解密。需理解公钥密码,清楚地分加密密钥和解密密钥是非常重要的。加密密钥是发送者加密时使用的,而解密密钥则是接收者解密时使用的。
3.加密密钥和解密密钥的区别
- 发送者只需要加密密钥
- 接收者只需要解密密钥
- 解密密钥不可以被窃听者获取
- 加密密钥被窃听者获取也没关系
也就是说,解密密钥从一开始就是由接收者自己保管的,因此只要将加密密钥发给发送者就可以解决密钥配送问题了,而根本不需要配送解密密钥。
非对称加密中,加密密钥一般是公开的。真是由于加密密钥可以任意公开,因此该密钥被称为公钥(pulickey)。相对地解密密钥是绝对不能公开的,这个密钥只能由你自己来使用,因此称为私钥(privatekey)。私钥不可以被别人知道,也不可以将它发送给别人。
公钥和私钥是"一一对应的",一对公钥和私钥统称为密钥对(keypair)。由公钥进行加密的密文,必须使用与该公钥配对的私钥才能解密。密钥对中的两个密钥之间具有非常密切的的关系(数学上的关系)。因此公钥和私钥不能分别单独生成。
PS:公钥密码的使用者需要生成一个包括公钥和私钥的密钥对,其中公钥会被发送给别人,而私钥则仅供自己使用。
二、非对称加密通信流程
举例:假设士兵A要给军官B发一条信息,A是发送者,B是接收者,黑客C想窃听A和B之间的通讯内容。
1.军官B生成一个包含公钥和私钥的密钥对(私钥由B自行妥善保管)
2.军官B将自己的公钥发送给士兵A,表示B请A用这个公钥对消息进行加密并发送给他。但此时公钥被黑客C截获(没关系,无伤大雅)。
3.士兵A用军官B的公钥对消息进行加密(加密后的消息只有B的私钥才能够解密。虽然A拥有B的公钥,但用B的公钥是无法对密文进行解密的)
4.士兵A将密文发送给军官B(密文也被黑客C截获,不过也没关系,C虽然拥有B的公钥,但是B的公钥是无法进行解密的)
5.军官B用自己的私钥对密文进行解密,获得最终的明文,详细可参考下图:
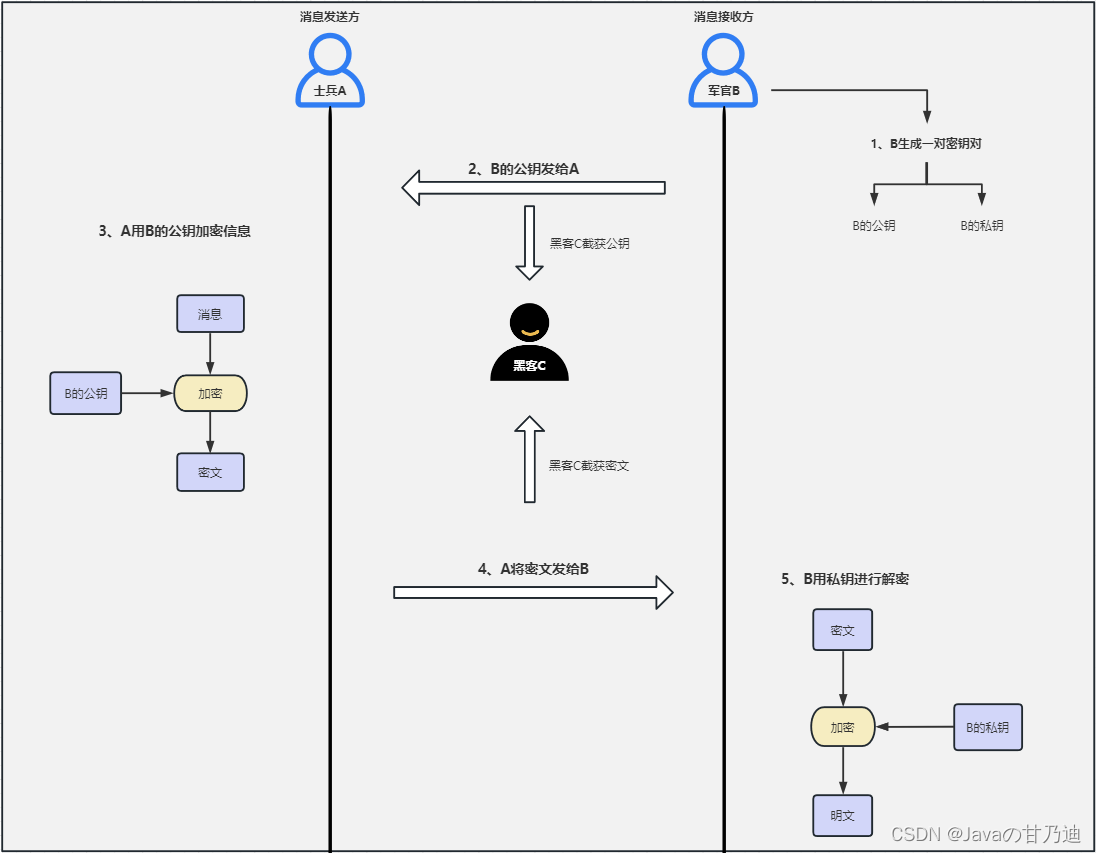
A和B之间传输的信息有两个,一个是B的公钥,一个是B公钥加密的密文,由于B的私钥没有出现在通信内容中,因此C无法对密文进行解密。
三、RSA非对称加密算法
RSA是一种非对称加密算法,它的名字由三位开发者。即RonRivest、AdiShamir和LeonardAdleman 的姓氏的首字母组成的(Rivest-Shamir-Leonard)。
1.RSA加密
RSA的加密工程可以用下来公式来表达,如下:

也就是说,RSA的密文是对代表明文的数字的E次方求modN的结果。换句话说,就是将明文自己做E次乘法,然后将其结果除以N求余数,这个余数就是密文。
RSA的加密是求明文的E次方modN,因此只要知道E和N这两个数,任何人都可以完成加密的运算。所以说E和N是RSA加密的密钥。也就是说E和N的组合就是公钥。
有一个很容易引起误解的地方需要大家注意一一E和N这两个数并不是密钥对(公钥和私钥的密钥对)。E和N两个数才组成了一个公钥,因此我们一般会写成 “公钥是(E,N)” 或者 “公钥是{E, N}" 这样的形式,将E和N用括号括起来。
2.RSA解密
RSA的解密和加密一样简单,可以用下面的公式来表达:
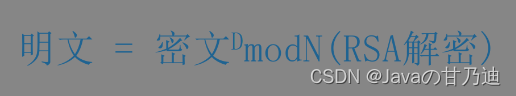
也就是说,对表示密文的数字的D次方求modN就可以得到明文。换句话说,将密文自己做D次乘法,在对其结果除以N求余数,就可以得到明文。
这里所使用的数字N和加密时使用的数字N是相同的。数D和数N组合起来就是RSA的解密密钥,因此D和N的组合就是私钥。只有知道D和N两个数的人才能够完成解密的运算。
大家应该已经注意到,在RSA中,加密和解密的形式是相同的。加密是求 "E次方的mod N”,而解密则是求 "D次方的modN”,这真是太美妙了。
当然,D也并不是随便什么数都可以的,作为解密密钥的D,和数字E有着相当紧密的联系。否则,用E加密的结果可以用D来解密这样的机制是无法实现的。
PS:顺便说一句,D是解密〈Decryption)的首字母,N是数字(Number)的首字母。
四、RSA工具类Util
RsaTestUtils.java
package com.st.microservice.billcenter.infrastructure.util;
import org.apache.commons.codec.binary.Base64;
import javax.crypto.BadPaddingException;
import javax.crypto.Cipher;
import javax.crypto.IllegalBlockSizeException;
import javax.crypto.NoSuchPaddingException;
import java.nio.charset.StandardCharsets;
import java.security.*;
import java.security.interfaces.RSAPrivateKey;
import java.security.interfaces.RSAPublicKey;
import java.security.spec.InvalidKeySpecException;
import java.security.spec.PKCS8EncodedKeySpec;
import java.security.spec.X509EncodedKeySpec;
import java.util.HashMap;
import java.util.Map;
/**
* @description: RSA加密工具类
* @author: admin
*/
public class RsaTestUtils {
public static void main(String[] args) {
//生成公钥和私钥
Map<Integer, String> keyMap = genKeyPair();
//加密字符串
String content = "我是原文啊!132456789";
System.out.println("加密前内容:" + content);
System.out.println("随机生成的公钥为:" + keyMap.get(0));
System.out.println("随机生成的私钥为:" + keyMap.get(1));
String messageEn = encrypt(content, keyMap.get(0));
System.out.println("加密后的内容为:" + messageEn);
String messageDe = decrypt(messageEn, keyMap.get(1));
System.out.println("还原后的内容为:" + messageDe);
}
/**
* 随机生成密钥对
*/
public static Map<Integer, String> genKeyPair() {
// KeyPairGenerator类用于生成公钥和私钥对,基于RSA算法生成对象
KeyPairGenerator keyPairGen = null;
try {
keyPairGen = KeyPairGenerator.getInstance("RSA");
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
}
// 初始化密钥对生成器,密钥大小为96-1024位
assert keyPairGen != null;
keyPairGen.initialize(1024, new SecureRandom());
// 生成一个密钥对,保存在keyPair中
KeyPair keyPair = keyPairGen.generateKeyPair();
// 得到私钥
RSAPrivateKey privateKey = (RSAPrivateKey) keyPair.getPrivate();
// 得到公钥
RSAPublicKey publicKey = (RSAPublicKey) keyPair.getPublic();
String publicKeyString = new String(Base64.encodeBase64(publicKey.getEncoded()));
// 得到私钥字符串
String privateKeyString = new String(Base64.encodeBase64((privateKey.getEncoded())));
// 将公钥和私钥保存到Map
Map<Integer, String> keyMap = new HashMap<>();
// 0表示公钥
keyMap.put(0, publicKeyString);
// 1表示私钥
keyMap.put(1, privateKeyString);
return keyMap;
}
/**
* RSA公钥加密
*
* @param str 加密字符串
* @param publicKey 公钥
* @return 密文
*/
public static String encrypt(String str, String publicKey) {
// base64编码的公钥
byte[] decoded = Base64.decodeBase64(publicKey);
RSAPublicKey pubKey;
String outStr = null;
try {
pubKey = (RSAPublicKey) KeyFactory.getInstance("RSA").generatePublic(new X509EncodedKeySpec(decoded));
Cipher cipher = Cipher.getInstance("RSA");
cipher.init(Cipher.ENCRYPT_MODE, pubKey);
outStr = Base64.encodeBase64String(cipher.doFinal(str.getBytes(StandardCharsets.UTF_8)));
} catch (InvalidKeySpecException | BadPaddingException | IllegalBlockSizeException | InvalidKeyException |
NoSuchPaddingException | NoSuchAlgorithmException e) {
e.printStackTrace();
}
// RSA加密
return outStr;
}
/**
* RSA私钥解密
*
* @param str 加密字符串
* @param privateKey 私钥
* @return 明文
*/
public static String decrypt(String str, String privateKey) {
//64位解码加密后的字符串
byte[] inputByte = Base64.decodeBase64(str.getBytes(StandardCharsets.UTF_8));
//base64编码的私钥
byte[] decoded = Base64.decodeBase64(privateKey);
RSAPrivateKey priKey;
//RSA解密
Cipher cipher;
String outStr = null;
try {
priKey = (RSAPrivateKey) KeyFactory.getInstance("RSA").generatePrivate(new PKCS8EncodedKeySpec(decoded));
cipher = Cipher.getInstance("RSA");
cipher.init(Cipher.DECRYPT_MODE, priKey);
outStr = new String(cipher.doFinal(inputByte));
} catch (InvalidKeySpecException | NoSuchAlgorithmException | NoSuchPaddingException | BadPaddingException |
IllegalBlockSizeException | InvalidKeyException e) {
e.printStackTrace();
}
return outStr;
}
}
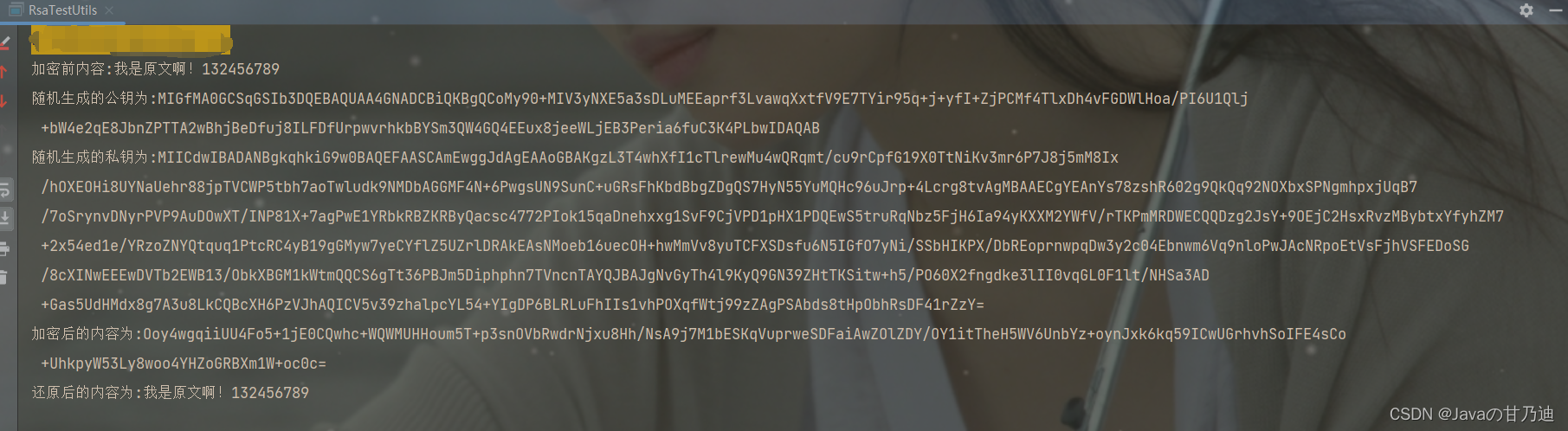
实例结果:
简单的应用场景: 先生成一对公私钥匙对,前端拿公钥加密,后端拿私钥解密。