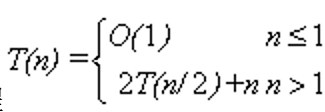Vrb是客观存在的,b相对于r的速度(从R到b的变化),右上角的b表示投影到p坐标系,只是表达数值的不同。
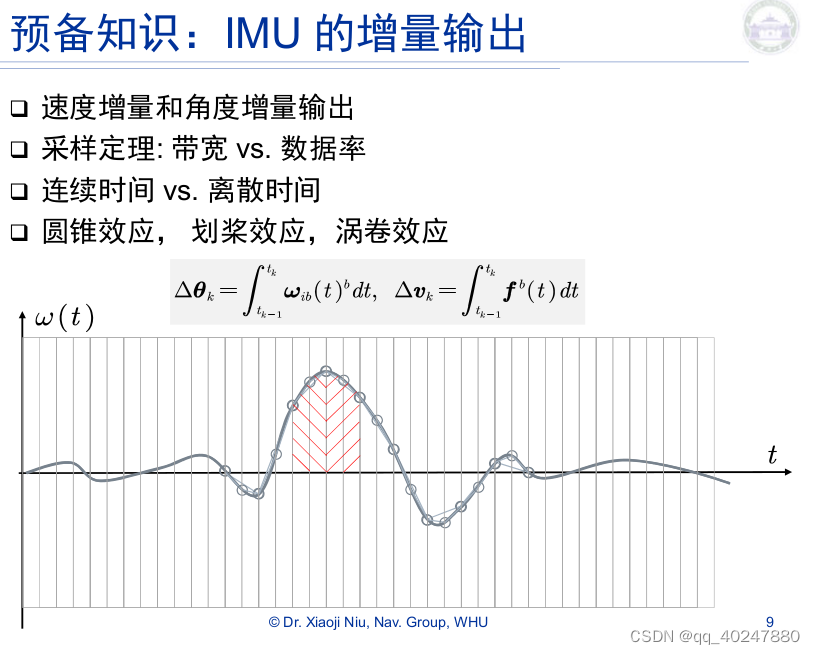
(工程上5-10,50倍)奈奎斯特采样率,香农采样定理,又称奈奎斯特采样定理,是信息论,特别是通讯与信号处理学科中的一个重要基本结论。1924年奈奎斯特(Nyquist)就推导出在理想低通信道的最高大码元传输速率的公式:理想低通信道的最高大码元传输速率B=2W,信息传输速率C=B*log2N 。(其中W是理想低通信道的带宽,N是电平强度)
模拟积分电路代替数字化后所处理积分角速度。电容两端的电压uc与流过电容的电流ic之间存在着积分关系。如能使电路的输出电压uo与电容两端的电压uc成正比,而电路的输入电压ul与流过电容的电流ic成正比,则uo与ul之间即可成为积分运算关系。利用理想运放工作在线性区时“虚短”和“虚断”的特点可以实现以上要求。
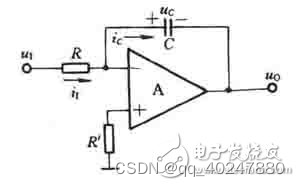
电路积分过程中之记录了积分面积,但是参考轴一直在运动。所以需要补偿圆锥划桨涡卷,对应姿态速度位置解算
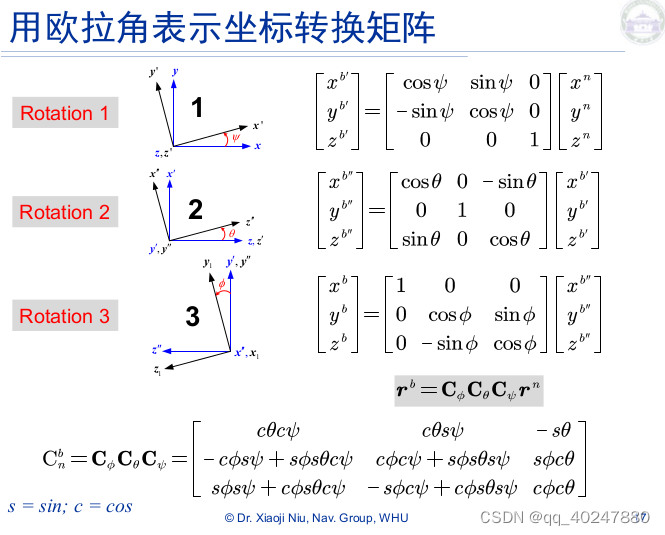
rotation2矩阵的sin正负号转置,因为z轴x转到y,y轴z到x反向了,x轴y到z的顺序

相对于的变化和坐标系转动(投影)是相反的。下面为n到b的变化量(向下),但是b系投影(旋转矩阵)到n系(角标向上看)。

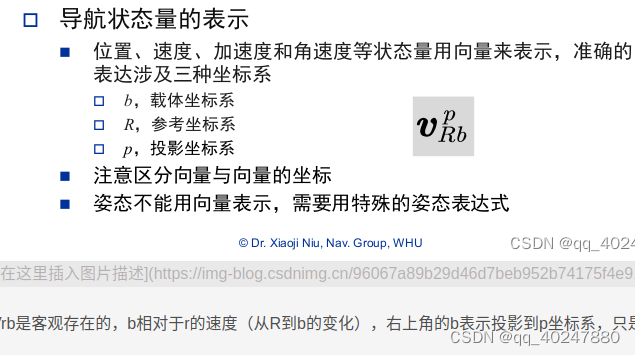

寺院书徐虚轴方向平行 共厄就是转置,四元数的逆就是矩阵求逆
共厄就是转置,四元数的逆就是矩阵求逆

Q^{R}_{b}表示从R转到b的四元数,能够将b参考系投影到R参考系
用途争辩
即使到目前为止四元数在某些领域的用途仍在争辩之中。一些哈密顿的支持者非常反对奥利弗·亥维赛的向量代数和约西亚·吉布斯的向量分析的发展,以维持四元数的超然地位。对于三维空间这可以讨论,但对于更高维四元数就失效了(但可用延伸如八元数和克利福德代数)。而事实上,在20世纪中叶的科学和工程界中,向量几乎已完全取代四元数的位置。
詹姆斯·克拉克·麦克斯韦曾经在他的《电磁场动力理论》(A Dynamical Theory of Electromagnetic Field)直接以20条有20个变量的微分方程组来解释电力、磁力和电磁场之间的关系。某些早期的麦克斯韦方程组使用了四元数来表述,但与后来亥维赛使用四条以向量为基础的麦克斯韦方程组表述相比较,使用四元数的表述并没有流行起来。
事实上,四元数是常被数学家称为几何代数的clifford代数的一个子代数,而后者已经得到很好的研究和应用,尤其是在理论物理中。例如可以用几何代数将狭义相对论和经典电动力学表述为非常优美的形式,量子力学中讨论自旋常用的泡利矩阵实际上也是几何代数的一个子代数的矩阵表示,类似的例子还有对经典力学中刚体的转动的不可交换性的表述。
应用
四元数大量用于计算机图形学中,表示三维对象的旋转及方位。四元数亦见于控制论、信号处理、姿态控制、物理、轨道力学和生物信息学,[1][2] 都是用来表示旋转和方位。
相对于另两种旋转表示法(矩阵和欧拉角),四元数具有某些方面的优势,如速度更快、提供平滑插值、有效避免万向锁问题、存储空间较小等等 [3]。

(中)是等效旋转矢量,theta是IMU积分项。近似2到3是因为两者差异是二阶小,一是(中)和theta都是小量,二是两者差异比较小。

最后一个公式。第一种理解,第一项为【1,0,0,0】,第二项为上一时刻的姿态,第三项为考虑地球自转,运动牵连角速度,body运动的角度,而不是IMU测量的Inertial到body的角度。第二种1理解是第一项是考虑innertial系到navigation系的角度,第二项为上一时刻,第三项只考虑IMU的测量。好处是第一项本身比较小,可以作定轴假设而误差不大,其次是更新频率可以变小。

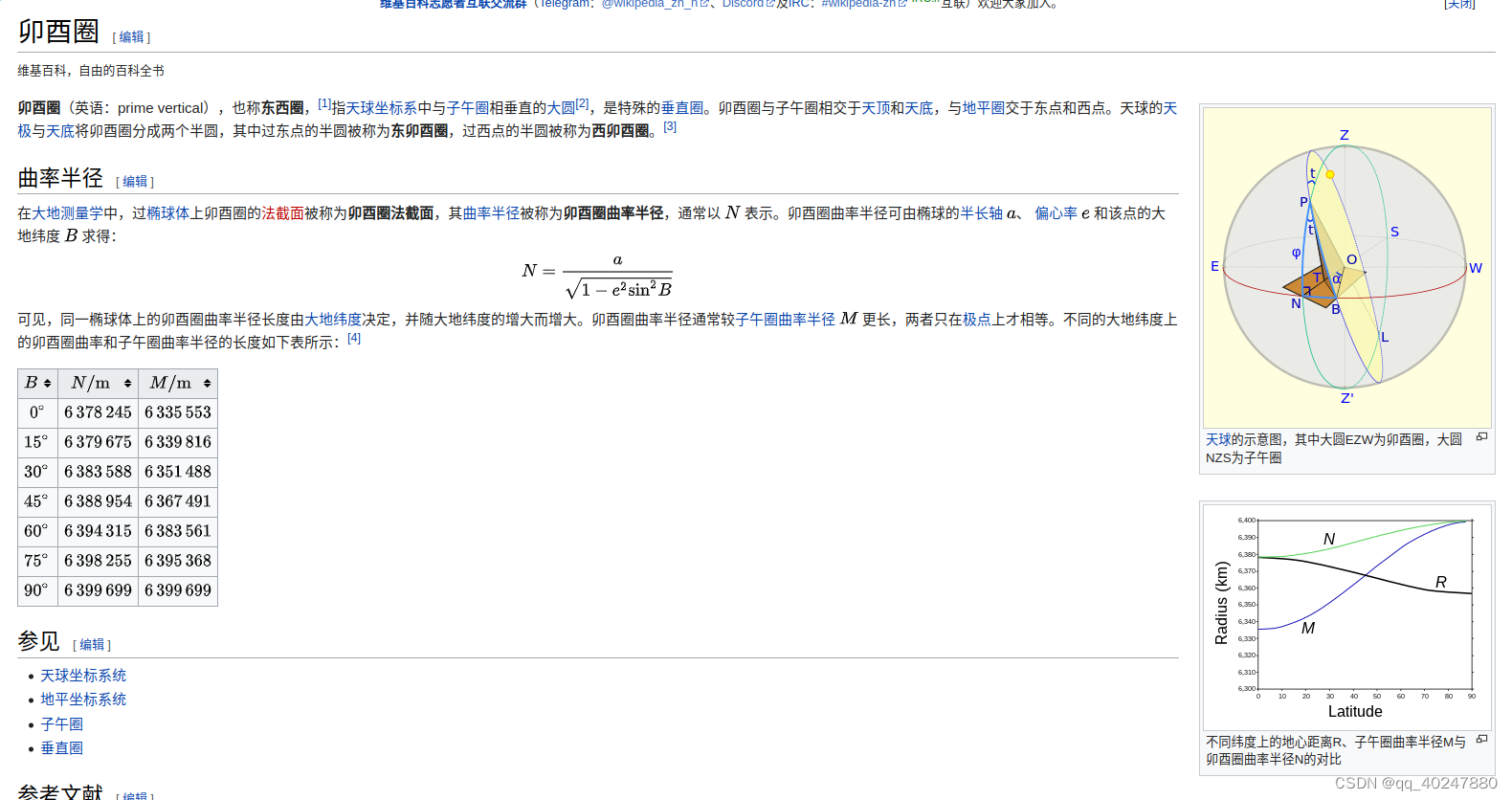
北东地,body向北运动时角速度向西负号,body向东运动会有向北的角速度和向天的角速度负号。导航坐标系用小写n,北向用大写N。式中 RM、RN 分别为载体所在位置的子午圈半径和卯酉圈半径。

卯酉[圈(英语:prime vertical),也称东西圈,[1]指天球坐标系中与子午圈](https://zh.wikipedia.org/zh- sg/%E5%8D%AF%E9%85%89%E5%9C%88)相垂直的大圆[2],是特殊的垂直圈。卯酉圈与子午圈相交于天顶和天底,与地平圈交于东点和西点。天球的天极与天底将卯酉圈分成两个半圆,其中过东点的半圆被称为东卯酉圈,过西点的半圆被称为西卯酉圈。[3] 在微分几何中,曲率的倒数就是曲率半径,即R=1/K。 平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。一个圆上任一圆弧的曲率半径恰好等于圆的半径。30degN6,383,588M6,351,488
通常分别表示横滚抚养偏航


哥式方程表达a和b坐标系之间有角速度的时候, 对速度的影响。比如b是地球坐标系e,a是宇宙坐标系i,公式相当于宇宙中的速度=汽车相对于地球的速度+地球自转X汽车位置向量


公式1到公式2是求导数得到。公式2到公式三交换了等号两边的项,公式2第一项由tips第三项代入,公式2第三项由黑板第三第四行加起来得到,第三行因为地球自转角速度从宇宙i观察不变所以导数为0,第四行代入tips第二行得到Ve地速+地球角速度叉乘运动距离,分配率展开得到黑板第五行。ppt公式3红色表示 (重力-角速度X宇宙视角下车的切向线速度)=(重力-车圆周运动下平行与赤道的向心加速度)=当地重力


蓝色是在线速度积分区间有角运动就会出现(旋转效益),绿色是积分区间出现线振动和角振动(划桨过程中,划桨效应)时数值比较明显,绿色在角速度和加速度存在但保持不变下会被抵消(叉乘顺序反向导致数值相同方向相反)