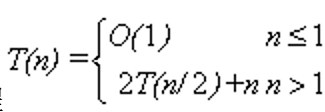1.f(x)与|f(x)|关系。

1.连续关系。(f(x)在"[a,b]上连续" => |f(x)|在"[a,b]连续")

①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. （因为f(x)在x0的连续点=>x0必为|f(x)|的连续点）

 注：”[a,b]连续“包括：
 ①f(x)在[a,b]连续
 ②f(x)在[a,b]上有界,且仅有有限间断点
 ③f(x)在[a,b]只有有限个第一类间断点。

证明：f(x)在"[a,b]上连续" => |f(x)|在"[a,b]连续"

2.可积关系。(f(x)可积 => |f(x)|可积)
证明略。
反例：
f(x)有无限个间断点，f(x)不可积。但是|f(x)|可积。

3.可导关系。
①f(x)在x0可导，则当f(x0) ≠ 0时
f(x)可导 <=> |f(x)|可导

②f(x)在x0可导，则当f(x0) = 0时，有两种情况。
-------1.若f’(x₀) = 0，则 <=> |f(x)| 在点x₀处可导，且|f’(x₀)|=0。
-------2.若f’(x₀) ≠ 0，则| f(x)|在点x₀处不可导
证明当f’(x0) ≠ 0时，不成立。

2.f(x)与f ’ (x)关系。

在有界区间(a,b)上有如下关系：
①f ‘（x）在(a,b)上有界 => f(x) 在(a,b)一定有界。
②f (x) 在（a,b）上无界 => f ’ (x)在（a,b）一定无界。
证明①：

在无界区间上没有确定性关系：
若f(x) = x,则f ’ (x) = 1在(a,+∞)有界，但f(x)在(a,+∞)无界。
若f(x) = sin²x,则f(x)在(a,+∞)有界，但是f ’ (x)在(a,+∞)无界。

3.f(x)与F(x)关系。

f(x)在(a,b)上有原函数F(x)，则在(a,b)上：
①f(x)不一定连续
②f(x)不一定时初等函数
③F(x)不一定时初等函数
④F’(x) = f(x),因此F(x)连续