NumPy 数组应用初探

news2024/11/24 6:36:30

  NumPy是Python中科学计算的基本包。它是一个Python库，提供了一个多维数组对象，各种派生对象（如屏蔽数组和矩阵），以及对数组进行快速操作的各种例程，包括数学、逻辑、形状操作、排序、选择、I/O、离散傅立叶变换、基本线性代数、基本统计操作、随机模拟等等。
  本文以二维数组为主体，以图文形式介绍 NumPy 的基本概念和操作。

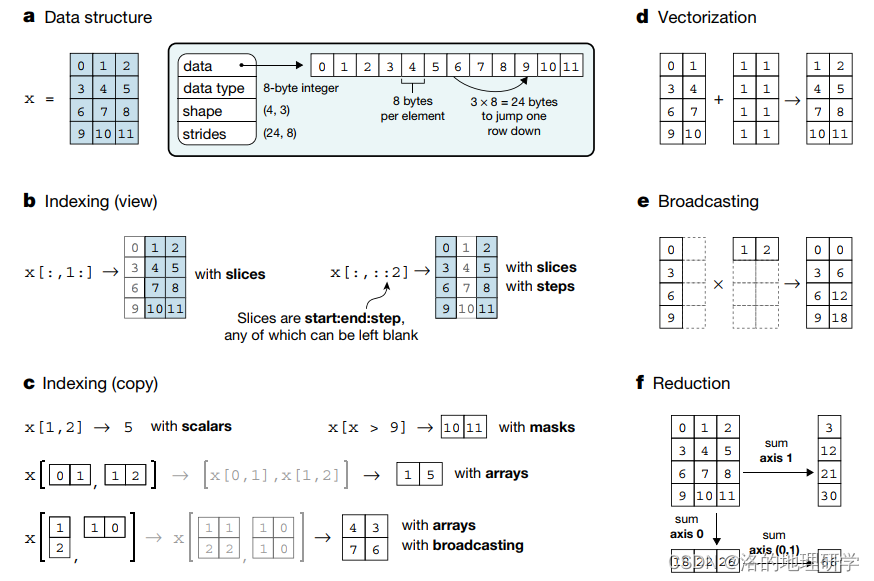
关于 NumPy 的 Nature 论文的主要图解

  论文地址：https://www.nature.com/articles/s41586-020-2649-2

NumPy 的几个基本数组概念图

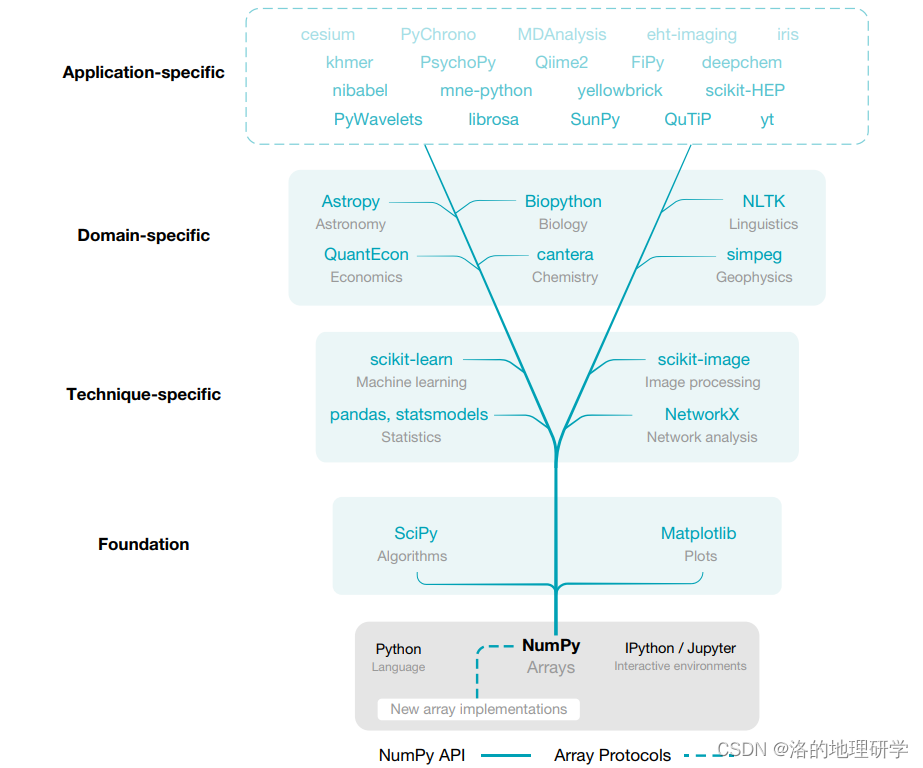
在这里插入图片描述

基于 NumPy 的 Python 数据与科学体系

在这里插入图片描述

数组基础

import numpy as np

数组创建

# 将 Python 列表转为数组
D1 = np.array([1,2,3])
# 创建 全 1 数组
D2 = np.ones(3)
# 创建 全 0 数组
D3 = np.zeros(3)
# 创建 全 2 数组
D4 = np.full(3, 2)
# 多维数组的创建类似。创建 2 × 3 的全 0 数组
D5 = np.zeros((2,3))

在这里插入图片描述

维度或轴

  NumPy 的 axis 定义了数组的维度或轴，并可通过 axis 对指定轴进行处理。NumPy 最多支持 32 个轴，也就是 32 维数据。
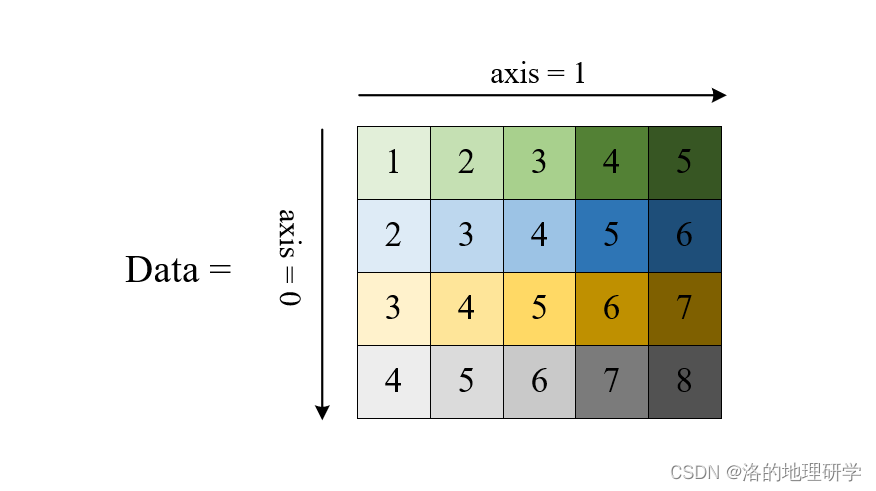
在这里插入图片描述

数组属性

属性说明示例结果
shape形状Data.shape(4, 5)
ndim维度Data.ndim2
dtype数据类型Data.dtype‘int32’
itemsize每个元素的大小(字节)Data.itemsize4
flags内存信息Data.flagsnumpy.core.multiarray.flagsobj
real实数部分Data.real[0, 0]1
imag虚数部分Data.imag[0, 0]0

数字型数组数据类型统计

名称描述范围识别码每个值内存占用（bytes）
bool8(bool_)布尔型True 或 False（0 或 1）b1
int88位整形-128 ~ 127i1
int1616位整形-32768 ~ 32767i2
int32(intc)32位整形-2147483648 ~ 2147483647i4
int6464位整形-9223372036854775808 ~ 9223372036854775807i8
uint88位无符号整形0 ~ 255u1
uint1616位无符号整形0 ~ 65535u2
uint32(uintc)32位无符号整形0 ~ 4294967295u4
uint6464位无符号整形0 ~ 18446744073709551615u8
float16半精度浮点数-65500.0 ~ 65500.0f2
float32单精度浮点数-3.4028235e+38 ~ 3.4028235e+38f4
float64(longdouble)双精度浮点数-1.7976931348623157e+308 ~1.7976931348623157e+308f8
complex64单精度复数由两个单精度浮点数（实部和虚部）组成c8
complex128(clongdouble)双精度复数由两个双精度浮点数（实部和虚部）组成c16

   此外， NumPy 还支持字符串、日期等非数字型数据，例如：object_、bytes_、str_、void、datetime64、timedelta64 等，这里不做列出。

数组操作

数组切片

  1. 取一个值
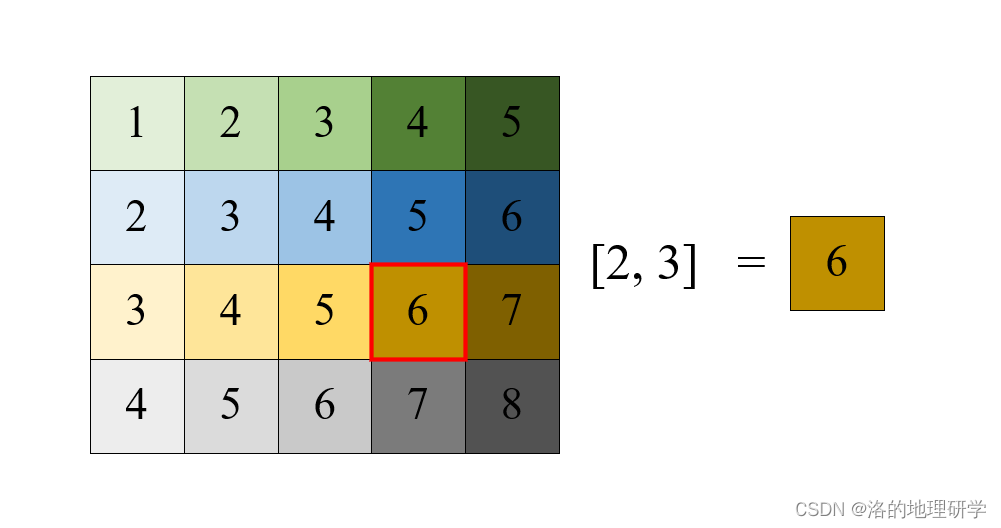
    在这里插入图片描述

  2. 取行（或列）——以取第一列为例
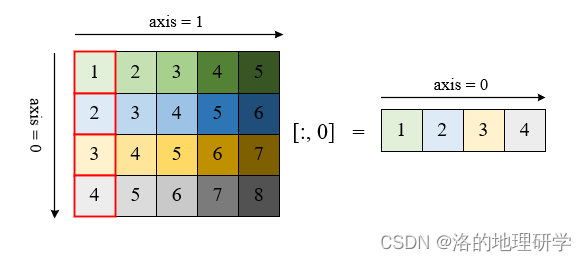
    在这里插入图片描述

上述取法丢失了维度。保留维度的取法如下：

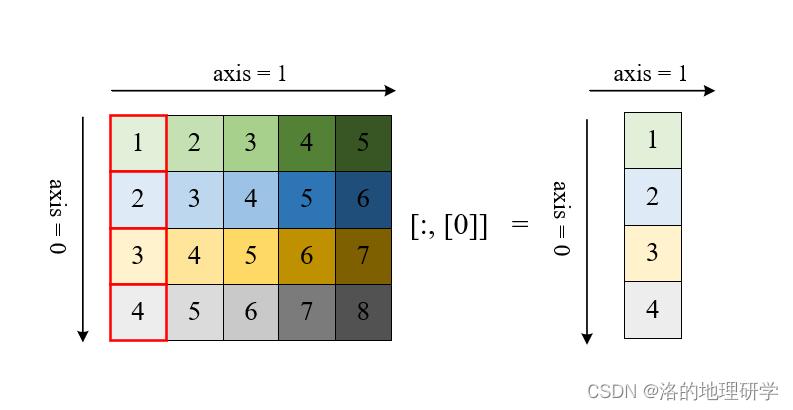
在这里插入图片描述

  1. 取部分区域
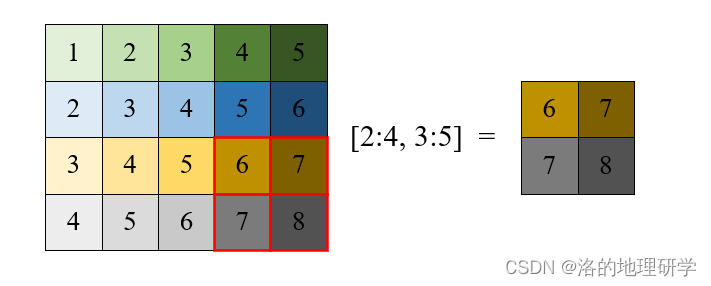
    在这里插入图片描述

  2. 花式切片
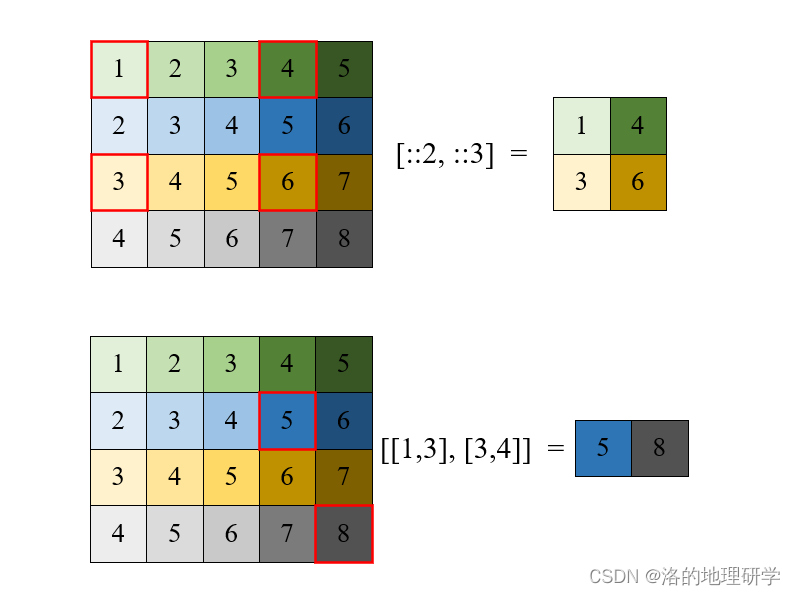
    在这里插入图片描述

形状变换

  1. 平铺数组
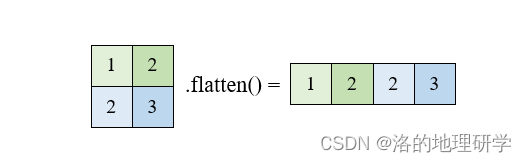
    在这里插入图片描述
  2. 转置数组
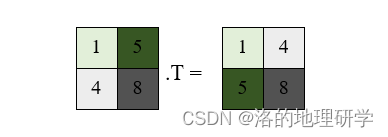
    在这里插入图片描述

更多维度可参考：
np.transpose （转置轴）
np.rollaxis （滚动轴）
np.moveaxis （移动轴）
np.swapaxes （交换轴）
np.expand_dims（增加空轴）
np.squeeze （清除空轴）

  1. 更改形状
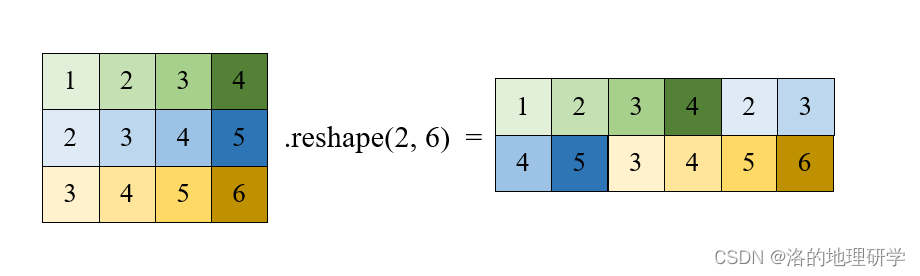
    在这里插入图片描述

其他相关方法：
np.resize （效果与 reshape 相同，但会修改原数据，慎用！）

  1. 反转数组

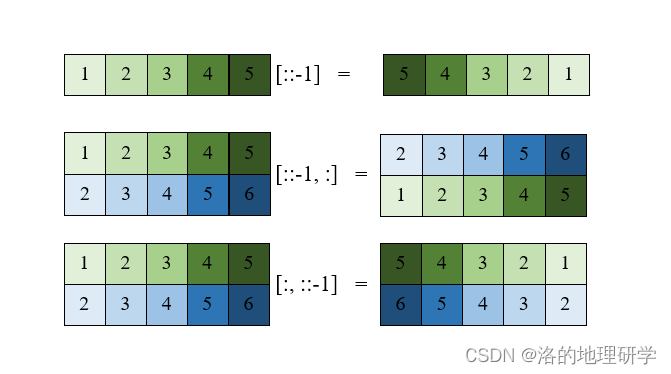
在这里插入图片描述

数组合并

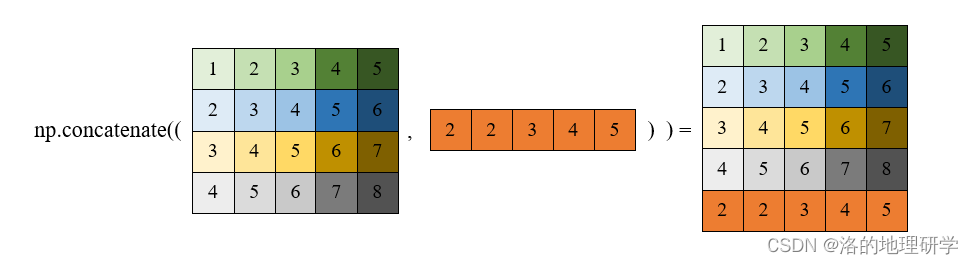
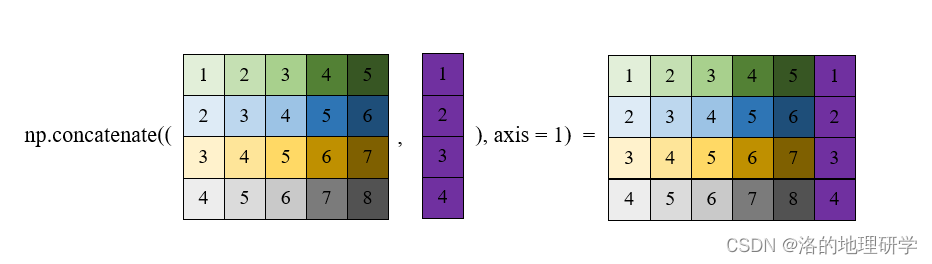
在这里插入图片描述

在这里插入图片描述

其他相关方法：
np.vstack （垂直堆叠）
np.hstack （水平堆叠）
np.stack （堆叠）
np.append（添加）
np.insert （插入）

数组扩展

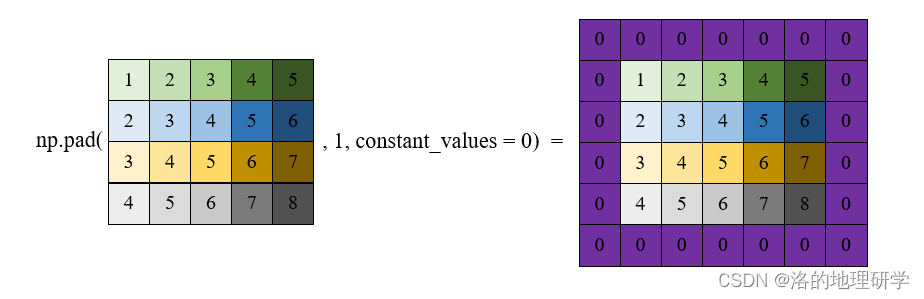
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

数组分割

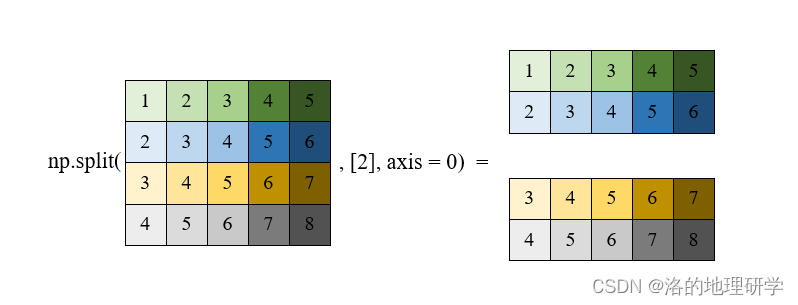
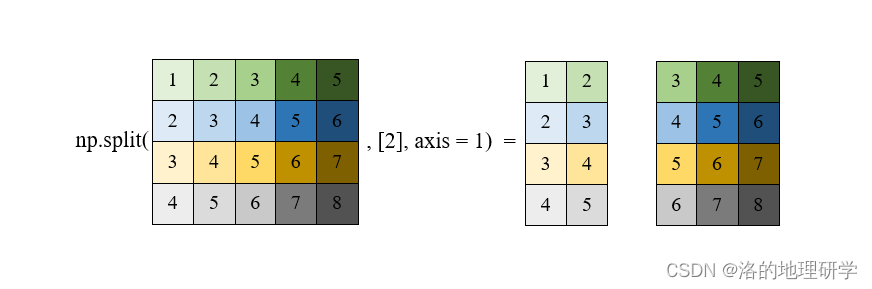
在这里插入图片描述
在这里插入图片描述

其他相关方法：
np.hsplit （水平分割）
np.vhsplit （垂直分割）
np.delete （删除）

掩膜数组

  被掩膜的值不会参与 NumPy 运算。
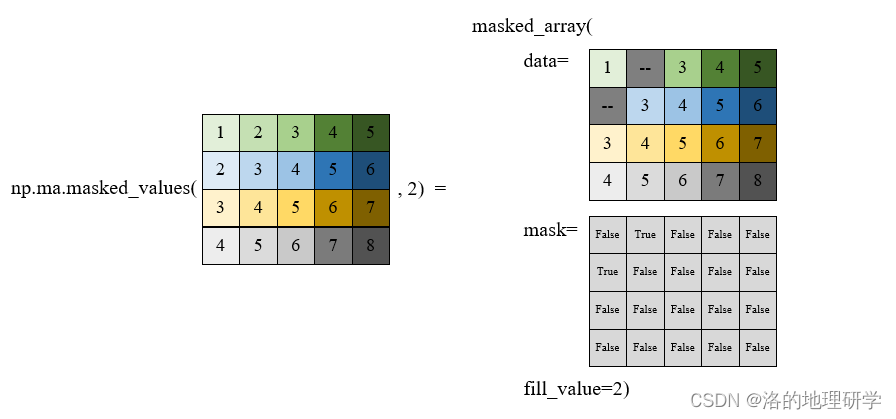
在这里插入图片描述

其他相关方法：
np.ma.masked_all
np.ma.masked_all_like
np.ma.masked_array
np.ma.masked_equal
np.ma.masked_greater
np.ma.masked_greater_equal
np.ma.masked_inside
np.ma.masked_invalid
np.ma.masked_less
np.ma.masked_less_equal
np.ma.masked_not_equal
np.ma.masked_object
np.ma.masked_outside
np.ma.masked_print_option
np.ma.masked_singleton
np.ma.masked_values
np.ma.masked_where

数组排序

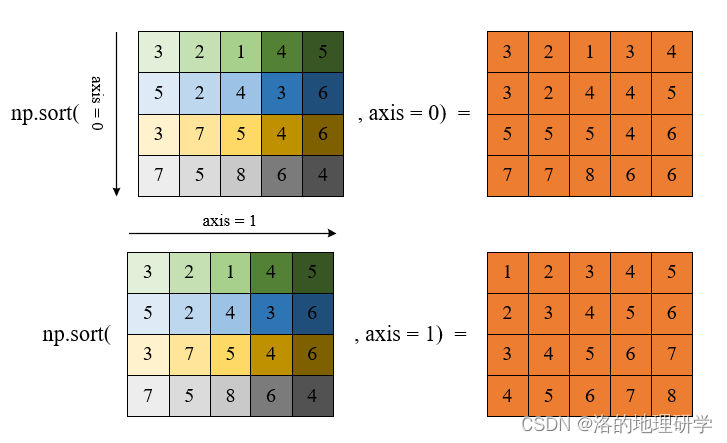
在这里插入图片描述

其他相关方法：
np.argsort （间接排序）
np.lexsort （多键排序）
np.searchsorted （查找排序）
np.partition （局部排序）

数学运算

算数运算

注意：参与运算的两个数带有维度（2维）（单个值除外）！

  1. 加、减、成、除（逻辑通用）（后同）
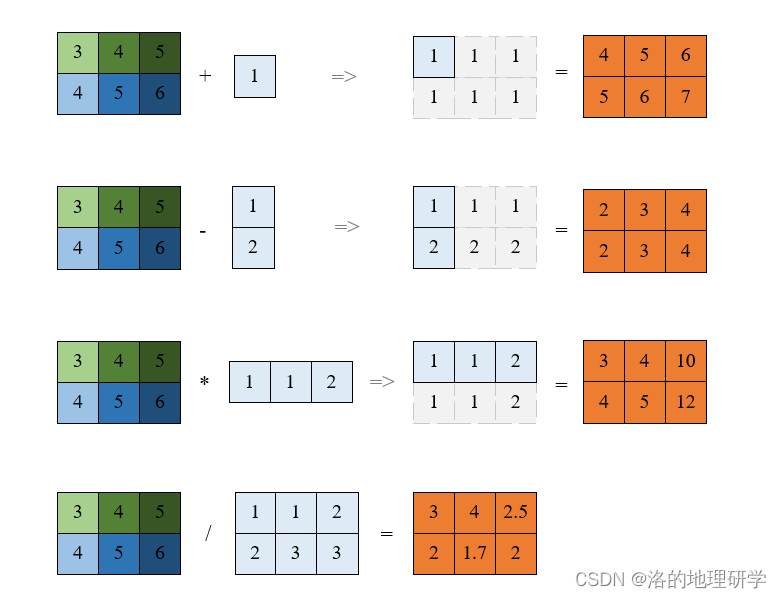
    在这里插入图片描述

其他相关方法：
np.add （加）
np.subtract （减）
np.multiply （成）
np.divide （除）

  1. 取余、取整
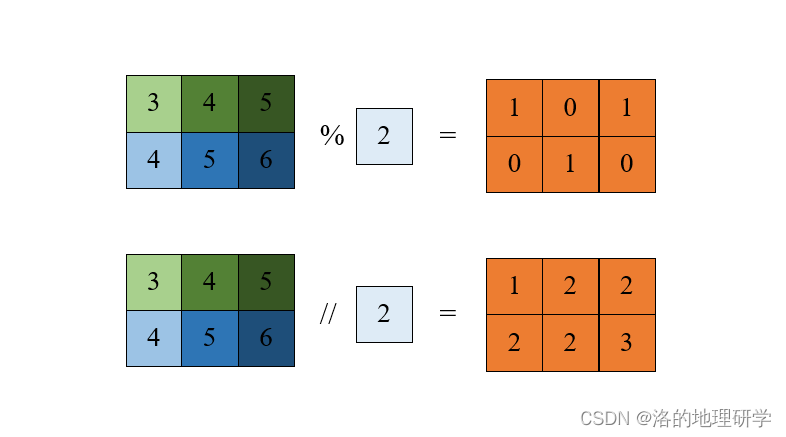
    在这里插入图片描述

其他相关方法：
np.mod （取余）
np.floor （向下取整）
np.ceil （向上取整）
np.round （四舍六入五成双）

  1. 其他运算

以乘方运算示例

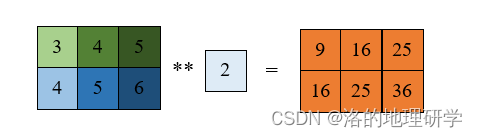
在这里插入图片描述

其他相关方法：
np.power（平方）
np.reciprocal（倒数）
np.sqrt（开平方）
…
三角函数类
np.sin （正弦函数）
np.cos （余弦函数）
…
弧度与角度
np.radians （角度转弧度）
np.degrees （弧度转角度）
…

  1. 特殊值
       NumPy 的浮点数具有两个特殊值，分别为 np.nan（非数字）、np.inf（无穷）。并具有以下特征：
  1. np.nan 与任何数运算都等于 np.nan，包括 0 。

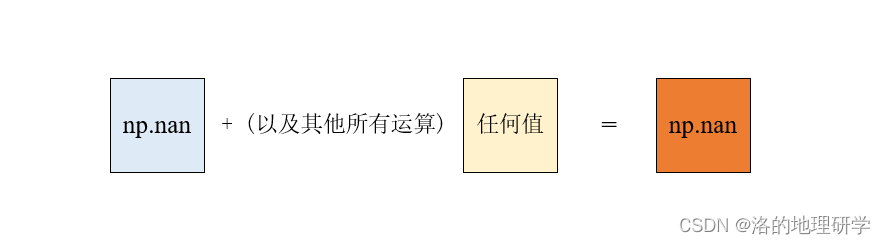
在这里插入图片描述

  1. np.nan 与任何其他数的逻辑运算均为 False，包括它自己。

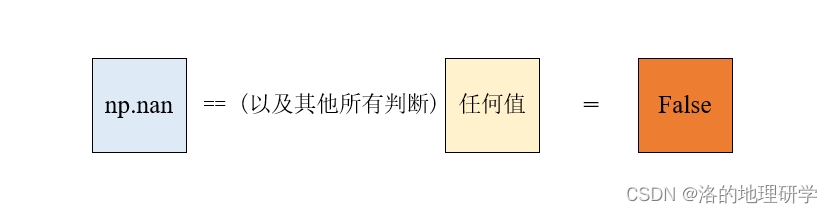
在这里插入图片描述

  1. -np.inf 小于任何值，np.inf 大于任何值（不包括它自己和 np.nan）

在这里插入图片描述

  1. -np.inf 与其他实数运算都等于-np.inf，np.inf 与其他实数运算都等于np.inf（不包括它自己和 np.nan）

在这里插入图片描述

  1. -np.inf 和 np.inf 的四则运算

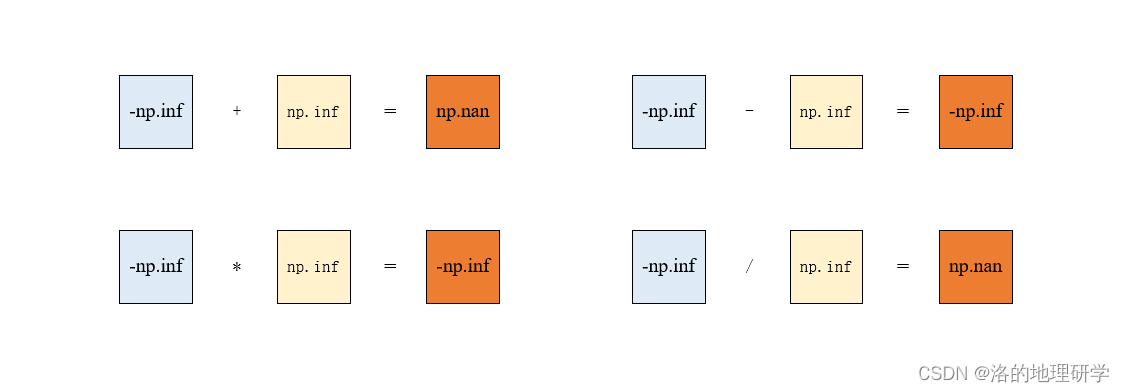
在这里插入图片描述

累积运算

以累积求和为例

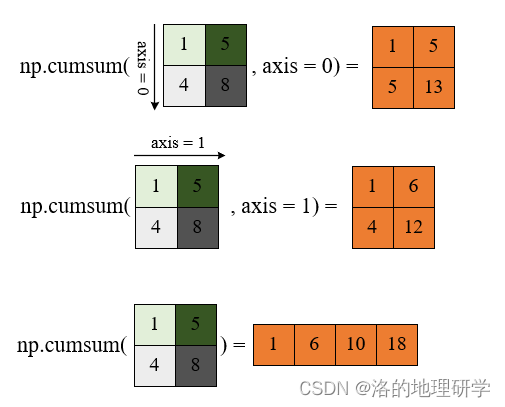
在这里插入图片描述

其他相关方法：
np.nancumsum （忽略 nan 的累积求和）
np.cumproduct（累积求积）
np.cumprod（累积求积）
np.nancumprod （忽略 nan 的累积求积）

统计计算

  1. 统计量
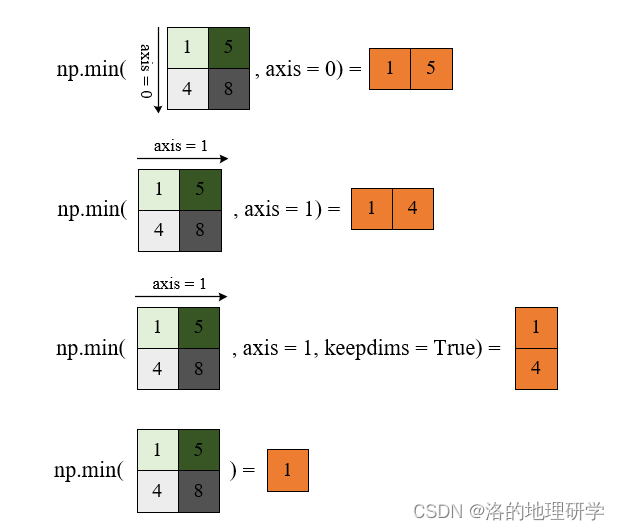
    在这里插入图片描述

其他统计量：
np.max （最大值）
np.mean（均值）
np.ptp （极差）
np.median （中位数）
np.sum（求和）
np.einsum （爱因斯坦求和约定）
np.prod（求积）
np.quantile （四分位数）
np.percentile （百分位数）
np.std （标准差）
np.var （方差）
…

逻辑判断

在这里插入图片描述

其他符号：<、<=、>=、==、!= …

矩阵运算

以矩阵乘法为例

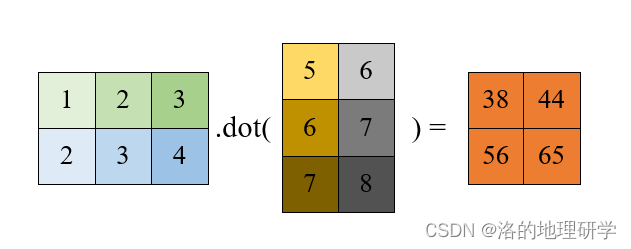
在这里插入图片描述

其他方法：
np.vdot （点积）
np.inner （内积）
np.outer （外积）
np.diag （取对角）
np.trace （迹）
np.matmul （矩阵乘积）
np.linalg.det （行列式）
np.linalg.inv （逆矩阵）
…

分段函数

在这里插入图片描述

其他方法：
np.where
np.select

数组与栅格

  对于地理科学而言，栅格数据是经常用到的一类数据，其本质上就是一个2维（单波段）或3维（多波段）数组 + 地理信息（坐标系/投影、仿射变换等）+ 其他元数据构成的一个数据集。

   本处以 gma 为例，说明数组与栅格数据的关系。详情请参考：地理与气象分析库。

   gma 库提供了栅格读取操作的全部过程，并提供标准化的栅格处理思路，可获取栅格数据的数据（数组）、地理信息和元数据，以及保存数据到栅格文件的全部流程。

单波段文件

   假设有一个1波段的 GTiff 栅格数据文件。

import gma
DataSet = gma.Open('XXX.tif')
Rows = DataSet.Rows
Columns = DataSet.Columns
Data = DataSet.ToArray()

  其数据部分的组织形式可以为：
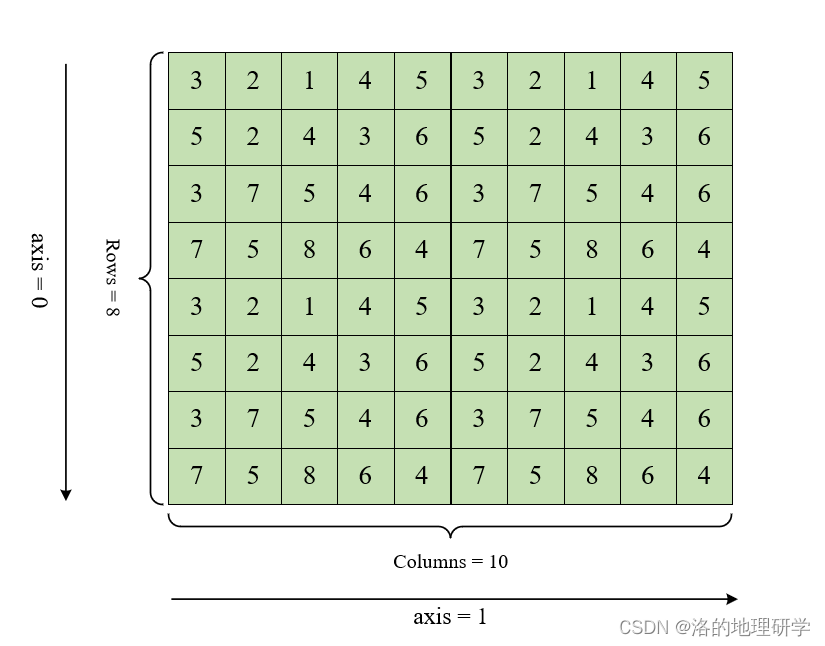
在这里插入图片描述

多波段文件

   假设有一个4波段的 GTiff 栅格数据文件。

import gma
DataSet = gma.Open('XXX.tif')
Rows = DataSet.Rows
Columns = DataSet.Columns
Bands = DataSet.Bands
Data = DataSet.ToArray()

   其数据部分的组织形式可以为：
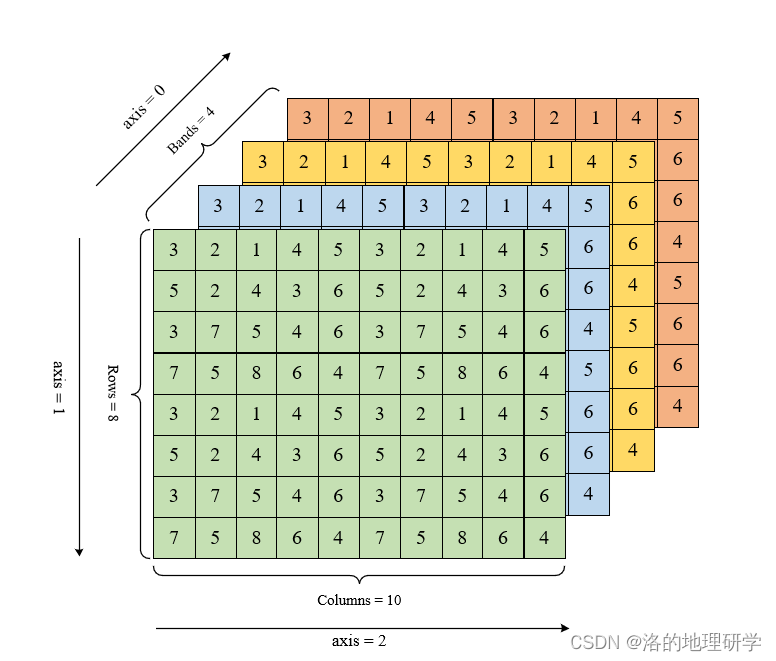
在这里插入图片描述

含有子数据集的科学数据集文件

   假设有一个含有2个子数据集的科学数据集（子数据集1包含4波段，子数据集2包含2个波段）的 netCDF 数据。

import gma
SDS = gma.Open('XXX.nc')
# 第一个子数据集（DataSet 1）
DataSet = SDS.GetSubDataSet(0)
Rows = DataSet.Rows
Columns = DataSet.Columns
Bands = DataSet.Bands
Data = DataSet.ToArray()
# 第二个子数据集（DataSet 2）类似，不做说明

并非所有的 netCDF 数据都含有子数据集！ 只具有 1 个子数据集的科学数据集需要以单波段或多波段栅格的方式读取。

   其数据部分的组织形式可以为：

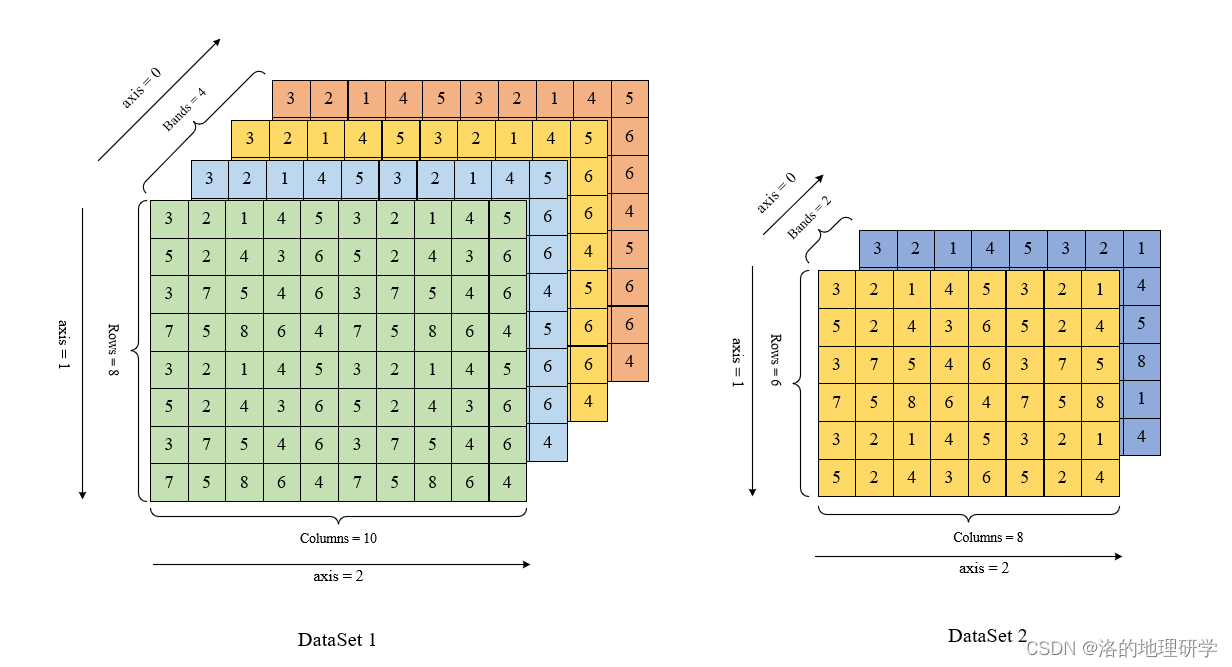
在这里插入图片描述

   此类数据每个数据集的组成数据（数组）的形状可能不同，因此无法一次性将所有数据读取为单一数组。gma 提供 子数据集类（SubDataSet），通过子数据集类分别获取每个数据集（DataSet），然后可利用普通栅格的方式读取和分析数据。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/47467.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Python-可视化单词统计词频统计中文分词

Python-可视化单词统计词频统计中文分词

可视化单词统计词频统计中文分词项目架构新建文件单词计数全文单词索引中文分词统计词频源代码项目架构 新建一个文件&#xff0c;输入文件的内容&#xff0c;查询此文件中关键字的出现的次数&#xff0c;关键字出现的位置&#xff0c;将所有的文本按照中文分词的词库进行切割…
阅读更多...
运筹说 第76期 | 最短路问题

运筹说 第76期 | 最短路问题

通过前面的学习&#xff0c;我们已经学会了图与网络问题中图的基本概念和最小树问题&#xff0c;本期小编带大家学习最短路问题。 一 最短路问题 最短路问题是网络理论中应用最广泛的问题之一。许多优化问题可以使用这个模型&#xff0c;如设备更新、管道敷设、线路安排、厂区…
阅读更多...
tensorboard attempted to bind to port 6006,but it was already in use

tensorboard attempted to bind to port 6006,but it was already in use

我尝试运行tensorboard是遇到错误 这篇博客给了两个解决方案&#xff1a;
阅读更多...
弹出 think-cell 许可证密钥窗口丨使用教程

弹出 think-cell 许可证密钥窗口丨使用教程

think-cell需要使用有效的许可证密钥才能运行。每次启动 Microsoft PowerPoint 或 Microsoft Excel 时&#xff0c;都会检查许可证密钥。若您的系统上找不到任何有效的许可证信息&#xff0c;或许可证密钥即将到期&#xff0c;则会显示 think-cell 许可证密钥对话窗口。 thin…
阅读更多...
UDP-糖，UDP-GlcNAc 5′-二磷酸尿嘧啶核苷-N-乙酰半乳糖胺二钠盐 UDP-N-acetylglucosamine

UDP-糖，UDP-GlcNAc 5′-二磷酸尿嘧啶核苷-N-乙酰半乳糖胺二钠盐 UDP-N-acetylglucosamine

产品名称&#xff1a; UDP-GlcNAc 5′-二磷酸尿嘧啶核苷-N-乙酰半乳糖胺二钠盐 UDP-N-acetylglucosamine 产地&#xff1a;西安 规格&#xff1a;1mg 5mg 10mg 纯度&#xff1a;99% 用途&#xff1a;仅用于科研 温馨提示&#xff1a;仅用于科研&#xff0c;不能用于人体…
阅读更多...
R语言法国足球联赛球员多重对应分析（MCA）

R语言法国足球联赛球员多重对应分析（MCA）

数据集 fooball球员在场上的位置 数据来自国际足联的视频游戏FIFA 。游戏的特点是在游戏的各个方面评价每个球员的能力。等级是量化变量&#xff08;介于0和100之间&#xff09;&#xff0c;但我们将它们转换为分类变量。所有能力都被编码在4个等级&#xff1a;1.低/ 2.平均/ …
阅读更多...
Spring、SpringMVC和SpringBoot

Spring、SpringMVC和SpringBoot

常用的java框架有: SSH组合 SpringMVCSpringHibernate SSM组合 SpringMVCSpringMybatis&#xff08;流行组合&#xff09; SpringBoot springCloud 权限管控框架 Shiro、SpringSecurity 一. 概念 1. Spring Spring是一个开源容器框架&#xff0c;可以接管web层&#xf…
阅读更多...
显卡---显卡驱动---CUDA---Cudnn

显卡---显卡驱动---CUDA---Cudnn

1. 背景 最近在follow百度的CAE这篇论文时&#xff0c;源码需要的环境为&#xff1a; python 3.7 cuda: 11.0 cudnn: 8.0.4 gcc 8.2 该版本要求与我目前使用的服务器上的CUDA版本不相符合。因此搜索了一篇国外小哥的文章&#xff0c;讲述了如何在一台服务器上安装多个CUDA和Cud…
阅读更多...
【MySQL】数据库机房架构与跨城容灾详解(实战篇)（MySQL专栏启动）

【MySQL】数据库机房架构与跨城容灾详解(实战篇)（MySQL专栏启动）

&#x1f4eb;作者简介&#xff1a;小明java问道之路&#xff0c;专注于研究 Java/ Liunx内核/ C及汇编/计算机底层原理/源码&#xff0c;就职于大型金融公司后端高级工程师&#xff0c;擅长交易领域的高安全/可用/并发/性能的架构设计与演进、系统优化与稳定性建设。 &#x1…
阅读更多...
平衡搜索树——红黑树小记

平衡搜索树——红黑树小记

文章目录红黑树定义规则操作规则平衡调整规则规则代码插入平衡调整代码左旋、右旋红黑树 定义 红黑树是一种 “平衡” 二叉 搜索树 “平衡”: 相比较于AVL树来说&#xff0c;是一种弱平衡 在红黑树中&#xff0c;任意从根到叶子的路径中&#xff0c;LEN(最长的路径)< 2*LE…
阅读更多...
Keras深度学习实战（39）——音乐音频分类

Keras深度学习实战（39）——音乐音频分类

Keras深度学习实战&#xff08;39&#xff09;——音乐音频分类0. 前言1. 数据集与模型分析1.1 数据集分析1.2 模型分析2. 歌曲流派分类模型2.1 数据加载与预处理2.2 模型构建与训练3. 聚类分析小结系列链接0. 前言 音乐音频分类技术能够基于音乐内容为音乐添加类别标签,在音乐…
阅读更多...
爬虫基本原理

爬虫基本原理

爬虫基本原理 网络爬虫的本质 爬虫是模仿用户在浏览器或者某个应用上的操作&#xff0c;把操作的过程实现自动化的程序 数据的传输是由客户端和服务器来进行交互的&#xff0c; 他们进行交互的层是传输层&#xff0c;遵守TIP/IP协议 我们在查询一个网址之后发生了四个步骤 …
阅读更多...
spring复习05,spring整合mybatis,声明式事务

spring复习05,spring整合mybatis,声明式事务

spring复习05,spring整合mybatis,声明式事务spring整合mybatis1. 在pom.xml中导入依赖2. 创建实体类3. 创建Mapper接口4. 配置mybatis核心配置文件5. 编写映射文件Mapper.xml6. 编写数据源配置7. sqlSessionFactory8. sqlSessionTemplate9. 需要给接口加实现类10. 将实现类注入…
阅读更多...
JavaScript获取DOM元素相关信息和属性

JavaScript获取DOM元素相关信息和属性

getBoundingClientRect 获取到元素盒模型的一些信息,得到的结果是没有单位的,不包含滚动条的距离,不包含margin&#xff0c;包含border和padding width 宽度&#xff08;包含边框&#xff09; height 高度&#xff08;包含边框&#xff09; left 从元素最左边到可视区最左边距…
阅读更多...
Ansible 企业级自动化运维实战

Ansible 企业级自动化运维实战

一、Ansible 简介 如果Ansible不采用0mq（ZeroMQ），在操作1000个以下的节点性能还可以，如果操作1000个以上的节点，性能就很差。 目前来说Ansible支持local，ssh，0mq，Ansible用ssh来管理被管理主机是最常见的方法。 saltstack简称salt，默认采用0mq（ZeroMQ），支持数万…
阅读更多...
[附源码]Python计算机毕业设计Django大学生心理健康测评系统

[附源码]Python计算机毕业设计Django大学生心理健康测评系统

项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等等。 环境需要 1.运行环境&#xff1a;最好是python3.7.7&#xff0c;…
阅读更多...
【Java】并发模式

【Java】并发模式

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pt4IAyjj-1669730661631)(https://gitee.com/github-25970295/blogpictureV2/raw/master/java-concurrent-overview-1.png)] 1. 并发问题的根源 可见性&#xff1a;一个线程对共享变量的修改&#xf…
阅读更多...
GIT error: Committing is not possible because you have unmerged files.

GIT error: Committing is not possible because you have unmerged files.

翻译&#xff1a;错误:无法提交&#xff0c;因为您有未合并的文件。 git 上传文件报错原因&#xff1a; 远程仓库的文件与在本地被删除了&#xff0c;本地删除文件后重新创建一个相同文件名的文件 远程仓库&#xff1a; 解决方法&#xff1a; 代码重新提交&#xff0c;重新合…
阅读更多...
xv6---Lab2: system calls

xv6---Lab2: system calls

目录 参考资料&#xff1a; 2.1 抽象物理资源 2.2 特权模式与系统调用 2.3 内核的组织 2.5 进程概览 2.6 Code: 启动xv6&#xff0c;第一个进程和系统调用 4.2 Trap from user space System call tracing 关于syscall函数的代码 每个syscall是由usys.pl自动生成为us…
阅读更多...
SAP 异常现象之同一个IDoc可以被POST两次触发2张不同的物料凭证

SAP 异常现象之同一个IDoc可以被POST两次触发2张不同的物料凭证

SAP 异常现象之同一个IDoc可以被POST两次触发2张不同的物料凭证 玩过SAP IDoc的童鞋都知道&#xff0c;一个IDoc正常情况下是只能被POST一次的&#xff0c;不可以POST两次的。 比如如下的IDoc 0000000205423126已经被POST了&#xff0c;其状态为53&#xff0c; Material Docume…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023