文章目录
- 红黑树
- 定义
- 规则
- 操作规则
- 平衡调整规则
- 规则
- 代码
- 插入
- 平衡调整代码
- 左旋、右旋
红黑树
定义
红黑树是一种 “平衡” 二叉 搜索树
“平衡”: 相比较于AVL树来说,是一种弱平衡
在红黑树中,任意从根到叶子的路径中,LEN(最长的路径)<= 2*LEN(最短的路径)
规则
- 红黑树中的结点:或红或黑
- 红黑树的根一定是黑色的
- 红黑树的“叶子结点”一定是黑色的。(此处的叶子: node == null)
- 红黑树中,任意路径(从根到叶子),红色不能和红色相邻
- 红黑树中,任意路径(从根到叶子),上面黑色结点的数量必须一样多
操作规则
查找操作:同普通的搜索树规则
插入操作:碰瓷“红色不能和红色相邻”这条规则——新插入的结点,一定是红色的
1.按照普通搜索树方式插入
2.判断是否破坏了红色不能红色相邻的规则,如果破坏了,则进行平衡调整操作
3.将根置为黑色
平衡调整规则
假设:新插入的结点(node)破坏了“红色不能相邻”的规则,且:
node的父节点: parent
node 的祖父结点: grandpa
node的叔叔结点: uncle(假如存在)
其中,node既可能是新插入的结点,也可能是不断向根回溯过程中的"grandpa"
根据红黑树定义及规则可知,以下成立:
- parent一定存在,且一定是红色
- grandpa一定存在,且一定是黑色
规则
1. uncle存在 && uncle的颜色是红色
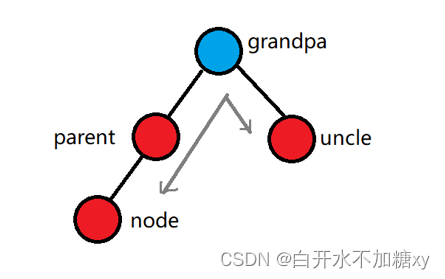
步骤:
- parent的颜色=黑色 uncle的颜色=黑色
- grandpa的颜色=红色
- 把 grandpa视为node,重新循环进行再平衡的过程,直到回溯到根上为止
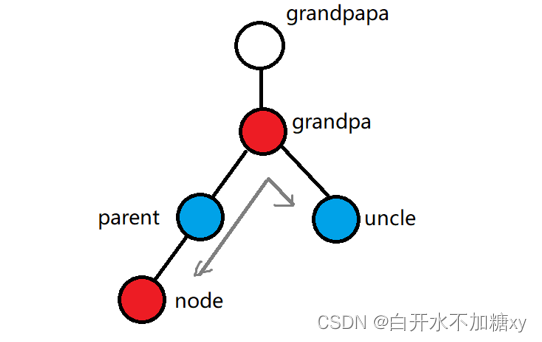
2.uncle 不存在或者(uncle存在&& uncle是黑色的)
(1) parent和grandpa的关系 与 node和parent的关系不一致

步骤

如果原来关系一致,不需要做此步骤。
3.关系一致后处理

优点
不改变路径上的黑色数量同时解决了parent和node红色相邻的问题
代码
插入
/**
* 保存红黑树的根结点
*/
public RBTreeNode root = null;
/**
* 保存红黑树中的结点个数
*/
public int size = 0;
/**
* 向红黑树中插入新的关键字
* @param key 关键字
* @return 是否插入成功
* true: 插入成功
* false: 插入失败(key 出现重复)
*/
public boolean insert(long key) {
// 1. 按照普通搜索树的方式进行插入
if (root == null) {
root = new RBTreeNode(key, null, BLACK);
size++;
return true;
}
RBTreeNode parent = null;
RBTreeNode current = root;
while (current != null) {
if (key == current.key) {
return false;
} else if (key < current.key) {
parent = current;
current = current.left;
} else {
parent = current;
current = current.right;
}
}
/**
* 根据插入规则,每次新插入的结点,一定是红色的
*/
RBTreeNode node = new RBTreeNode(key, parent, RED);
if (key < parent.key) {
parent.left = node;
} else {
parent.right = node;
}
size++;
/**
* 进行红黑树规则的判断 + 平衡调整过程
*/
adjustBalance(node);
return true;
}
平衡调整代码
private void adjustBalance(RBTreeNode node) {
while (true) {
RBTreeNode parent = node.parent;
if (parent == null) {
break;
}
if (parent.color == BLACK) {
break;
}
/**
* 一定破坏了"红色不能相邻"的规则
*/
RBTreeNode grandpa = parent.parent;
// 找到叔叔结点
if (parent == grandpa.left) {
RBTreeNode uncle = grandpa.right;
if (uncle != null && uncle.color == RED) {
/**
* 情况1:叔叔存在 并且 叔叔的颜色是红色
* 步骤:
* 1. 叔叔和父亲的颜色改成黑色
* 2. 祖父的颜色改成红色
* 3. 把祖父视为 node,再去判断是否违反规则了
*/
parent.color = uncle.color = BLACK;
grandpa.color = RED;
node = grandpa;
continue;
} else {
// 判断 grandpa <-> parent 和 parent <-> node 的关系是否不一致
// 已知 parent 是 grandpa 的左边
if (node == parent.right) {
leftRotate(parent);
//swap(parent, node);
parent = node;
}
// 接下来统一处理关系一致的情况
rightRotate(grandpa);
grandpa.color = RED;
parent.color = BLACK;
break;
}
} else {
RBTreeNode uncle = grandpa.left;
if (uncle != null && uncle.color == RED) {
/**
* 情况1:叔叔存在 并且 叔叔的颜色是红色
* 步骤:
* 1. 叔叔和父亲的颜色改成黑色
* 2. 祖父的颜色改成红色
* 3. 把祖父视为 node,再去判断是否违反规则了
*/
parent.color = uncle.color = BLACK;
grandpa.color = RED;
node = grandpa;
continue;
} else {
// 判断 grandpa <-> parent 和 parent <-> node 的关系是否不一致
// 已知 parent 是 grandpa 的右边
if (node == parent.left) {
rightRotate(parent);
//swap(parent, node);
parent = node;
}
// 接下来统一处理关系一致的情况
leftRotate(grandpa);
grandpa.color = RED;
parent.color = BLACK;
break;
}
}
}
/**
* 无论之前是什么情况,统一把根改成黑色
* 走到此处时,root 一定不是 null
*/
root.color = BLACK;
}
左旋、右旋
与AVL树左旋右旋原理一致。可参考上篇博客中左旋调整平衡部分。

private void leftRotate(RBTreeNode m) {
// m 代表图中的 b 结点
// parent 代表 b 结点可能存在的父亲
RBTreeNode parent = m.parent;
// right 代表图中的 a 结点
RBTreeNode right = m.right;
// leftOfRight 代表图中的可能存在的乙子树的根结点
RBTreeNode leftOfRight = right.left;
/*
其中: m != null && right != null
但是: parent 不保证 !null, leftOfRight 不保证 !null
*/
right.parent = parent; // 蓝色线的关系
// 黑色线的关系
if (parent == null) {
// m 是 root
root = right;
} else {
if (m == parent.left) {
parent.left = right;
} else {
parent.right = right;
}
}
right.left = m; // 黑色线的关系
m.parent = right; // 蓝色线的关系
m.right = leftOfRight;
if (leftOfRight != null) {
leftOfRight.parent = m;
}
}
private void rightRotate(RBTreeNode m) {
RBTreeNode parent = m.parent;
RBTreeNode left = m.left;
RBTreeNode rightOfLeft = left.right;
left.parent = parent;
if (parent == null) {
root = left;
} else {
if (m == parent.left) {
parent.left = left;
} else {
parent.right = left;
}
}
left.right = m;
m.parent = left;
m.left = rightOfLeft;
if (rightOfLeft != null) {
rightOfLeft.parent = m;
}
}


![[附源码]Python计算机毕业设计Django大学生心理健康测评系统](https://img-blog.csdnimg.cn/af1d473e76f342d1bbc88f0cf1b235f9.png)