通过前面的学习，我们已经学会了图与网络问题中图的基本概念和最小树问题，本期小编带大家学习最短路问题。

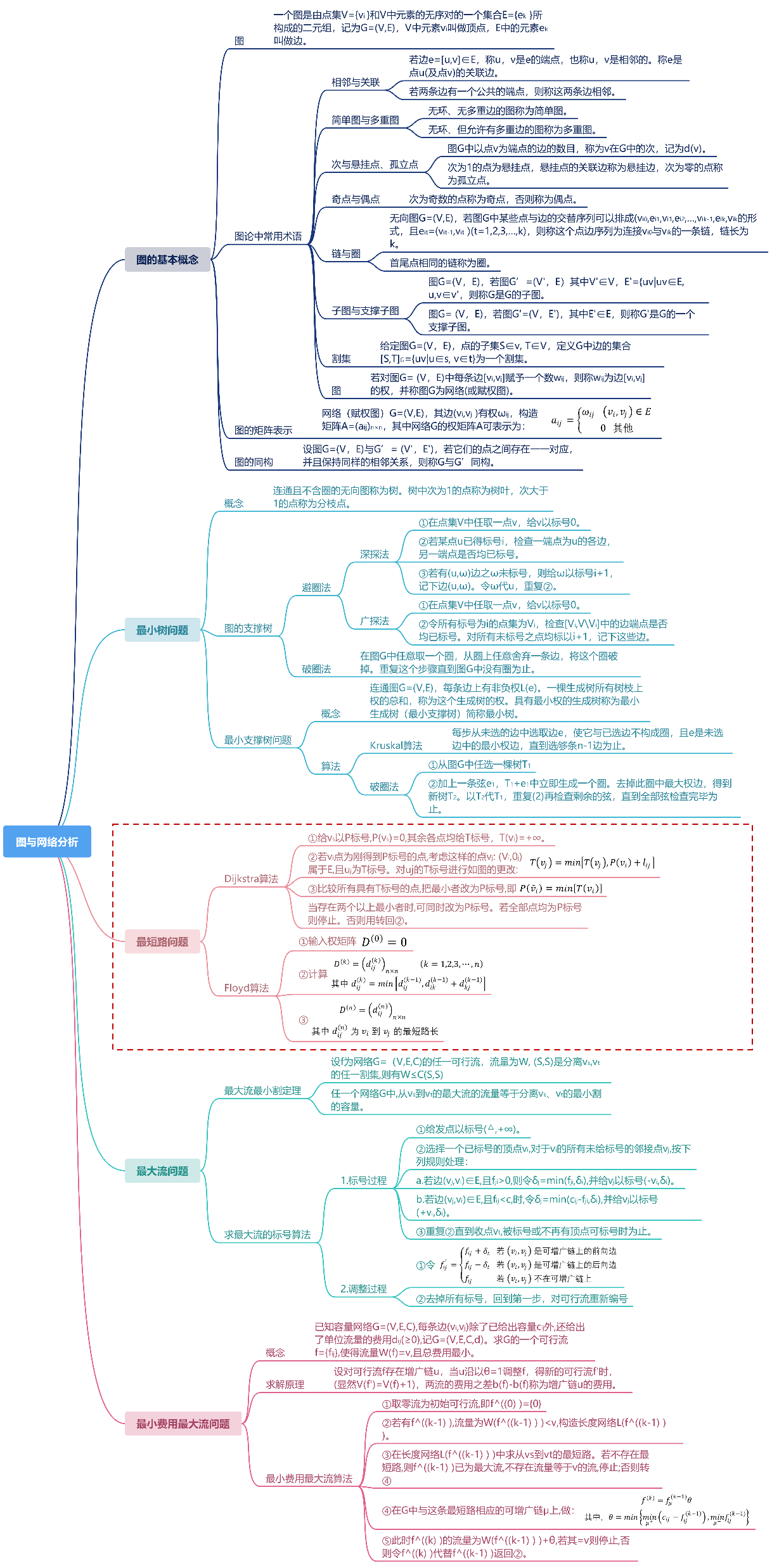
一 最短路问题

最短路问题是网络理论中应用最广泛的问题之一。许多优化问题可以使用这个模型，如设备更新、管道敷设、线路安排、厂区布局等。

最短路问题的一般提法如下:设G=(V,E)为连通图，图中各边（vi,vj）有权lij(lij=∞表示vi,vj间无边)，vs,vt为图中任意两点，求一条道路μ，使它是从vs到vt的所有路中总权最小的路。即:L(μ)=Σ（vi，vj）∈μlij最小。

有些最短路问题也可以是求网络中某指定点到其余所有结点的最短路，或求网络中任意两点间的最短路。下面我们介绍两种算法，可分别用于求解这几种最短路问题。

二 Dijkstra算法

01基本思想

Dijkstra算法由Dijkstra于1959年提出，可用于求解指定两点vs,vt间的最短路，或从指定点vs到其余各点的最短路，目前被认为是求无负权网络最短路问题的最好方法。

算法的基本思路基于以下原理：若序列{vs，v1，...vn-1,vn}是从vs到vn的最短路，则序列{vs，v1，...vn-1}必为从vs到vn-1的最短路。

02算法基本步骤

 🕛 给始点vs以P标号，P(vs)=0，其余节点均给T标号，T(vi)=+∞(i=2,3,…,n)。

 🕒 设节点vi为刚得到P标号的点，考虑点vj：(vi,vj)∈E,且vj为T标号。对vj的T标号进行如下修改:

T(vj)=min[T(vj),P(vi)+lij]

 🕕 比较所有具有T标号的节点，把T标号最小者改为P标号，即:P(vk)= min[T(vi)]

当存在两个以上最小者时，可同时改为P标号。若全部节点均为P标号，则算法停止，否则用vk代替vi，返回步骤2。每一步迭代将一个点的标号修改为P标号的同时，记录路径。

03应用

案例1

例1：用Dijkstra算法求图中点v1到点v8的最短路。

解：

(1)首先给v1以P标号，P(v1）=0，给其余所有点T标号：T(vi)=+∞，（i=2,3,...8）

(2)考虑v1邻点

T(v2)=min[T(v2),P(v1)+l12]=min[+∞,0+4]=4

T(v3)=min[T(v3),P(v1)+l13]=min[+∞,0+6]=6

(3)比较所有T标号，T(v2)最小，令P(v2)=4，并记录路径(v1,v2)。

T(v4)=min[T(v4),P(v2)+l24]=min[+∞,4+5]=9

T(v5)=min[T(v5),P(v2)+l25]=min[+∞,4+4]=8

(4)比较所有T标号，T(v3)最小，令P(v3)=6，并记录路径(v1,v3)。

(5)考虑v3邻点

T(v4)=min[T(v4),P(v3)+l34]=min[9,4+6]=9

T(v5)=min[T(v5),P(v3)+l35]=min[8,6+7]=8

(6)比较所有T标号，T(v5)最小，令P(v5)=8，并记录路径(v2，v5)。

(7)考虑v5邻点

T(v6)=min[T(v6),P(v5)+l56]=min[+∞,8+5]=13

T(v7)=min[T(v5),P(v5)+l57]=min[+∞,8+6]=14

(8)比较所有T标号，T(v4)最小，令P(v4)=9， 并记录路径(v2,v4)。

(9)考虑v4邻点

T(v6)=min[T(v6),P(v4)+l46]=min[13,9+9]=13

T(v7)=min[T(v7),P(v4)+l47]=min[14,9+7]=14

(10)比较所有T标号，T(v6)最小，令P(v6)=13, 并记录路径(v5,v6)。

(11)考虑v6邻点

T(v7)=min[T(v7),P(v6)+l67]=min[14,13+5]=14

T(v8)=min[T(v8),P(v6)+l68]=min[+∞,13+4]=17

(12)比较所有T标号，T(v7)最小，令P(v7)=14, 并记录路径(v5,v7)。

(13)考虑v7邻点

T(v8)=min[T(v8),P(v7)+l78]=min[17,14+1]=15

(14)因为只有一个T标号T(v8)最小，令P(v8)=15,并记录路径(v7,v8)，v1到v8最短路为:v1→v2→v5→v7→v8。

★Dijkstra法实际应用分析

①能够一次算出从起点到其他各节点的最短路径；

②计算效率不高，速度较慢，所需存储空间多，在大规模规划中受到一定限制；

③Dijkstra算法仅适合于所有的权wij ≥0的情形。如果当赋权有向图中存在有负权弧时，则算法失效。

案例2 设备更新问题

某工厂使用一台设备，每年年初工厂都要作出决定，如果继续使用旧的，要付较多维修费；若购买一台新设备，要付购买费。试制订一个5年的更新计划，使总支出最少。由表知该设备在各年的购买费，及在不同役龄的残值与维修费。

解：用点vi表示第i年年初购进一台新设备，虚设一个点v6，表示第5年年底。

       边(vi,vj)表示第i年初购进的设备一直使用到第j年年初(即第j-1年年底)。

边(vi,vj)上的数字表示第i年初购进设备后，一直使用到第j年初所需支付的购买、维修净费用。

       例如(v1,v2)边上的数字12=(第一年购买的费用11)+(一年的维修费用5)-(一年役龄机器的残值4)，同理计算得到其他数字。

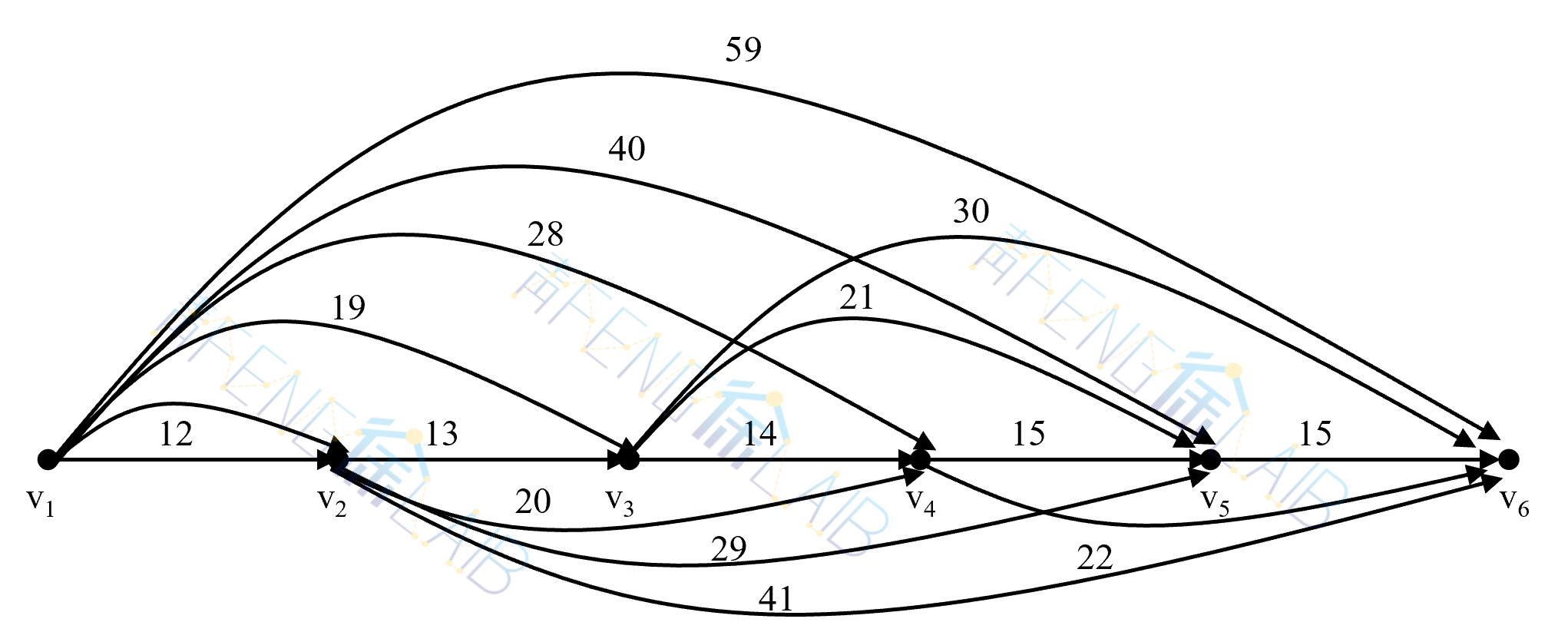
这样设备更新问题就变为:求从v1到v6的最短路问题。

(1)首先给v1以P标号，P(v1）=0，给其余所有点T标号：T(vi)=+∞，（i=2,3,...6）

(2)考虑v1邻点

T(v2)=min[T(v2),P(v1)+l12]=min[+∞,0+12]=12

T(v3)=min[T(v3),P(v1)+l13]=min[+∞,0+19]=19

T(v4)=min[T(v4),P(v1)+l14]=min[+∞,0+28]=28

T(v5)=min[T(v5),P(v1)+l15]=min[+∞,0+40]=40

T(v6)=min[T(v6),P(v1)+l16]=min[+∞,0+59]=59

(3)比较所有T标号，T(v2)最小，所以P(v2)=12，并记录路径(v1，v2)。

(4)考虑v2邻点

T(v3)=min[T(v3),P(v2)+l23]=min[19,12+13]=19

T(v4)=min[T(v4),P(v2)+l24]=min[28,12+20]=28

T(v5)=min[T(v5),P(v2)+l25]=min[40,12+29]=40

T(v6)=min[T(v6),P(v2)+l26]=min[59,12+41]=53

(5)比较所有T标号，T(v3)最小，令P(v3)=19，并记录路径(v1,v3)。

(6)考虑v3邻点

T(v4)=min[T(v4),P(v3)+l34]=min[28,19+14]=28

T(v5)=min[T(v5),P(v3)+l35]=min[40,19+21]=40

T(v6)=min[T(v6),P(v3)+l36]=min[53,19+30]=49

(7)比较T标号，T(v4)最小，令P(v4)=28，并记录路径(v1,v4)。

(8)考虑v4邻点

T(v5)=min[T(v5),P(v4)+l45]=min[40,28+15]=40

T(v6)=min[T(v6),P(v4)+l46]=min[49,28+22]=49

(9)比较所有T标号，T(v5)最小，令P(v5)=40, 并记录路径(v1,v5)。

(10)考虑v5邻点

T(v6)=min[T(v6),P(v5)+l56]=min[49,40+15]=49

(11)因为只有一个T标号T(v6)，令P(v6)=49,并记录路径(v3,v6)，计算结束。

计算结果表明:v1→v3→v6为最短路，路长为49。即在第一年、第三年初各购买一台新设备为最优决策，这时5年的总费用为49。

案例3 选址问题 

某连锁企业在某地区有6个销售点，已知该地区的交通网络如图所示，其中点代表销售点，边表示公路，lij为销售点间公路距离，问仓库应建在哪个小区，可使离仓库最远的销售点到仓库的路程最近?

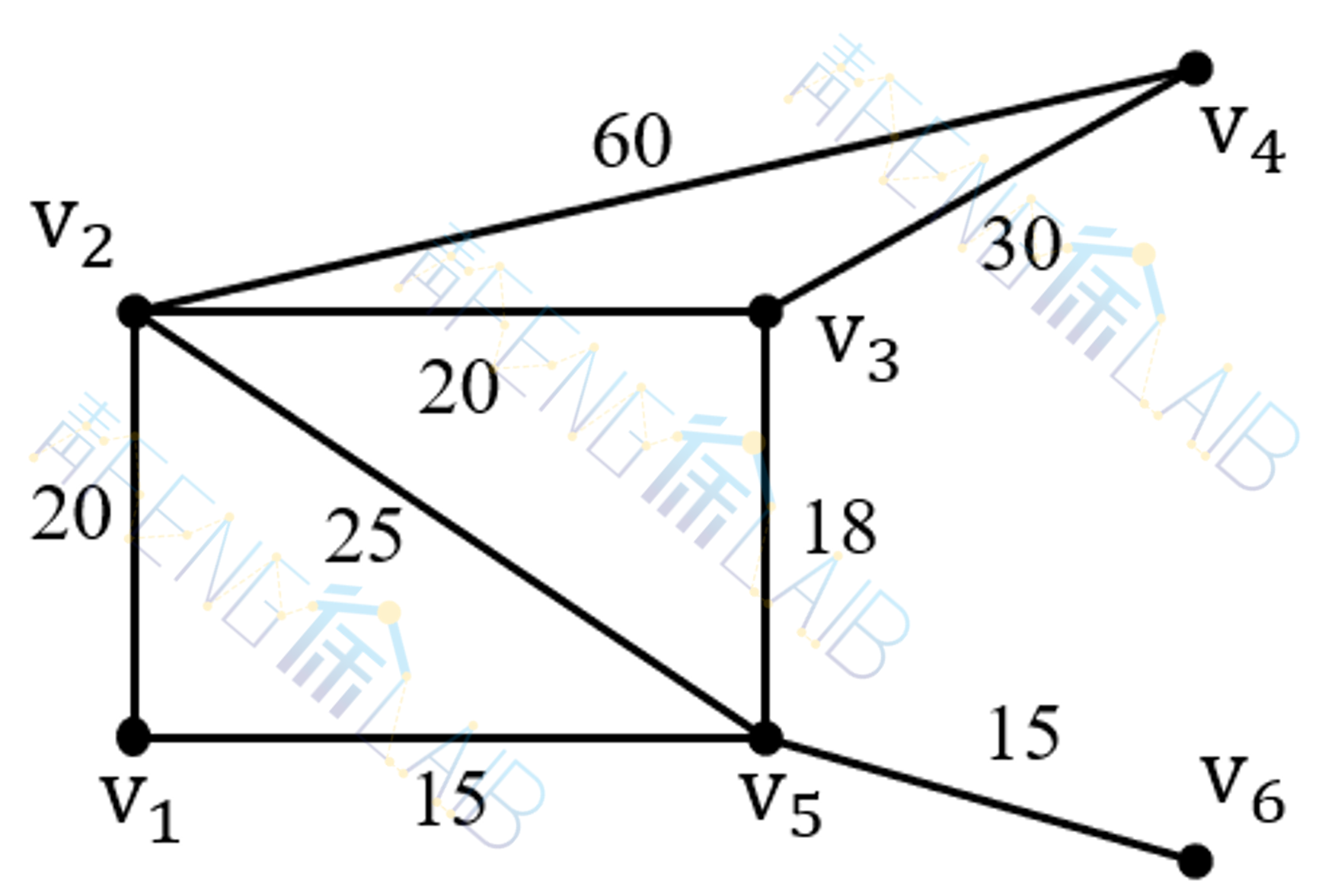
解：此问题实际要求出图的中心，可以化为一系列求最短路问题。

先求出v1到其他各点的最短路长dj，令D(v1)=max(d1,d2,…,d6)，表示若仓库建在v1，则离仓库最远的销售点距离为D(v1)。再依次计算v2,v3,…,v6到其余各点的最短路，每一次计算都是以此最小路问题，以D(v1)为例：

(1)首先给v1以P标号，P(v1）=0，给其余所有点T标号：T(vi)=+∞，（i=2,3,...6）

(2)考虑v1邻点

T(v2)=min[T(v2),P(v1)+l12]=min[+∞,0+20]=20

T(v5)=min[T(v5),P(v1)+l15]=min[+∞,0+15]=15

(3)比较所有T标号，T(v5)最小，所以P(v5)=15。

(4)考虑v5邻点

T(v2)=min[T(v2),P(v5)+l25]=min[20,15+25]=20

T(v3)=min[T(v3),P(v5)+l35]=min[+∞,15+18]=33

T(v6)=min[T(v6),P(v5)+l56]=min[+∞,15+15]=30

(5)比较所有T标号，T(v2)最小，令P(v2)=20。

(6)考虑v2邻点

T(v3)=min[T(v3),P(v2)+l23]=min[33,20+20]=33

T(v4)=min[T(v4),P(v2)+l24]=min[+∞,20+60]=80

(7)比较所有T标号，T(v6)最小，令P(v6)=30，v6邻点仅有v5，再比较其余T标号，T(v3)最小，令P(v3)=33。

(8)考虑v3邻点

T(v4)=min[T(v4),P(v3)+l34]=min[80,33+30]=63

(9)比较所有T标号，T(v4)最小，令P(v4)=63。由此得到：

d1=0，d2=20，d3=33

d4=63，d5=15，d6=30

所以：D(v1)=max(d1,d2,…,d6)=63

同理可求出D(v2),D(v3),…,D(v6)，D(vi)(i=1,…,6)中最小者即为所求，计算结果见下表：

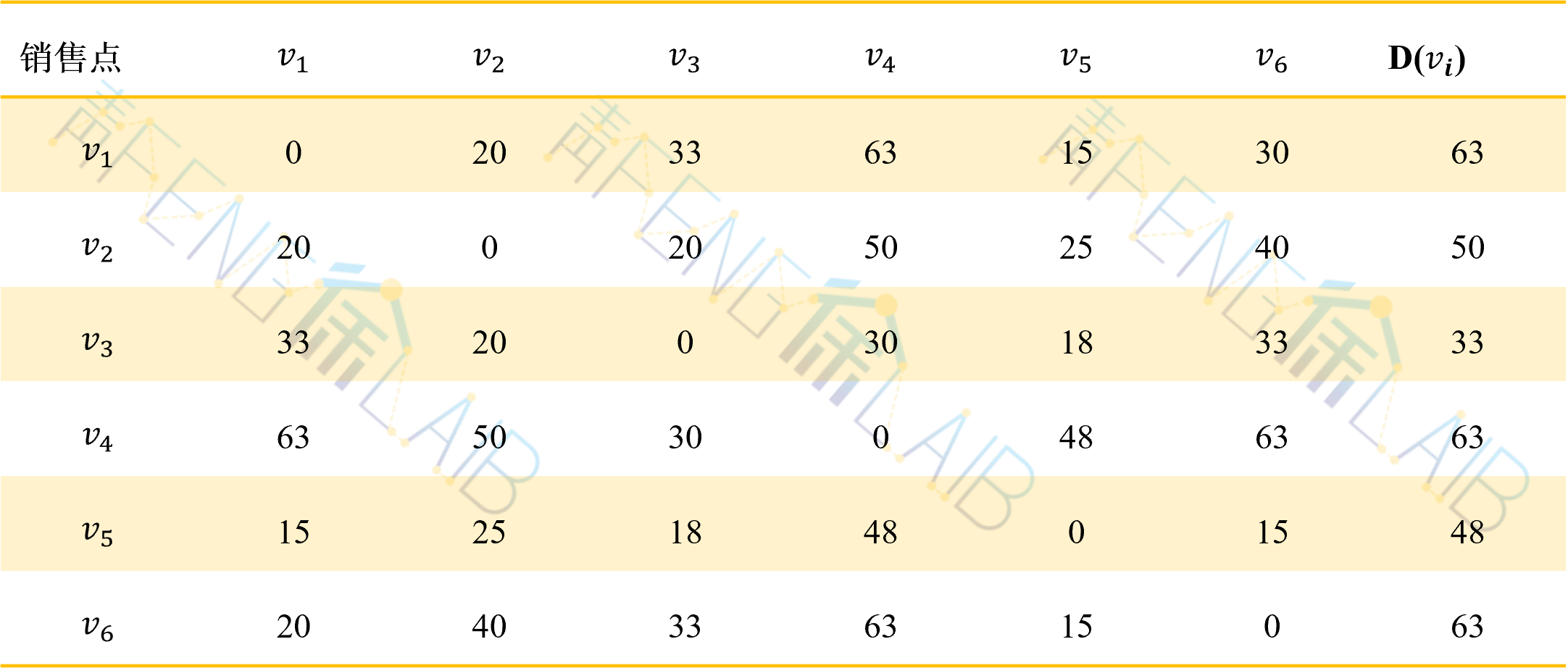
由于D(v3)=33最小，所以仓库应建在v3，此时离仓库最远的销售点(v1和v6)距离为33。

三 Floyd算法

01基本思想

某些问题是要求解网络上任意两点间最短路，这类问题可以用Dijkstra算法依次改变起点的办法计算，但比较繁琐。而Floyd方法可直接求出网络中任意两点间的最短路。

Floyd算法的思想是将n个节点的网络表示为n行n列的矩阵，而矩阵中的元素(i,j)表示从节点i到节点j的距离uij，如果两点直接没有边相连，则相应的元素就是无穷(∞)。

求解过程中依次把各个节点当成每对点之间的中间点，在加入中间点以后，判断新的路径是不是比原来的短，如果比原来的短，进行替换，直到得到两个节点之间的最短距离。

02算法基本步骤

为了计算方便，令网络的权矩阵为U=( uij )nxn，uij为vi到vj的距离，其中

令S=(sij )nxn , sij为vi到vj的路径上第一条弧的终点。

（1）初始时，对于任意两个顶点，若它们之间存在边，则以此边上的权值作为它们之间的最短路径长度，若不存在有向边，则以∞作为它们之间的最短路径长度。

以此输入权矩阵U(0)=U，并输入S(0)=(sij (0))nxn , sij (0)=j (i,j=1,2,3,..,n )，此时vi到vj的路径上第一条弧的终点为j。

（2）在原路径中加入顶点v1作为中间顶点，如果增加中间顶点后，得到的路径比原来的路径短，则以此新路径代替原路径，从而得到：

U(1)=(uij (1）)nxn，uij(1)=min[uij(0）,uik(0)+ukj(0)]是从vi到vj路径中的最短路长度，路径的中间点只允许为v1。

S(1)=(sij (1))nxn , sij (1)=1或j ，代表此时vi到vj的路径上第一条弧的终点可能是1也可能是j。

（3）以此类推，之后逐步尝试在原路径中加入k个顶点作为中间顶点，以更短的新路径代替原路径。

由此得到：U(k) = (uij(k))nxn (k=1,2,3,..,n)，其中uij(k)=min[uij(k-1),uik(k-1)+ukj(k-1)]是从vi到vj路径中的最短路长度，路径的中间点只允许为v1,v2,...vk。

S(k)=(sij (k))nxn  (k=1,2,3,..,n)

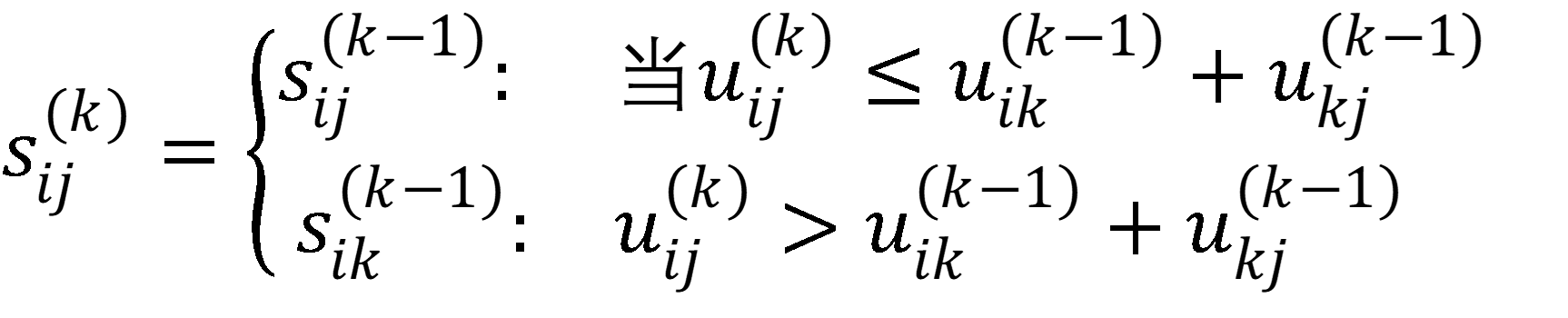
即若新的路径长于原路径，vi到vj的路径上第一条弧的终点不变；若新的路径短于原路径，vi到vj的路径上第一条弧的终点为：加入k-1个顶点作为中间顶点后，vi到vk的路径上第一条弧的终点。

（4）当k=n时

U(n)=(uij(n))nxn，uij(n)就是vi到vj的最短路路长。

S(n)=(sij(n))nxn ，sij(n)是vi到vj的最短路第一条弧的终点。

03应用

案例4

求如下网络中各点对间最短路的路长。

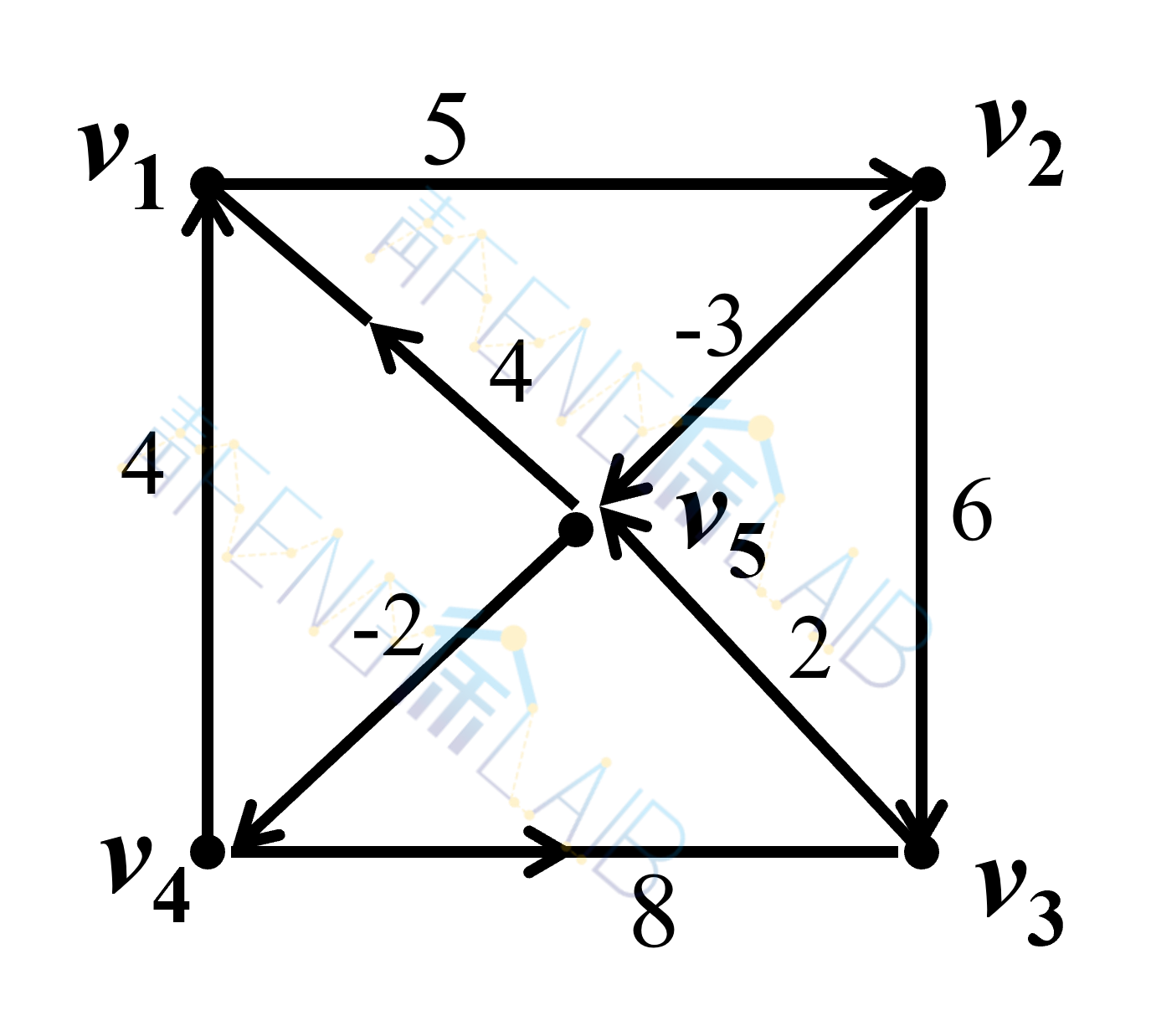
解：

用U(0)的第一行、第一列来修正其余的uij，即作：uij(1)=min[uij(0),ui1(0)+u1j(0)]

同时，在修正uij(1)处修改Sij(1)=Si1(0)，v1成为每对点之间的中间点，如v4→v2路径变为v4→v1→v2，其第一段弧与v4→v1的第一段弧相同。

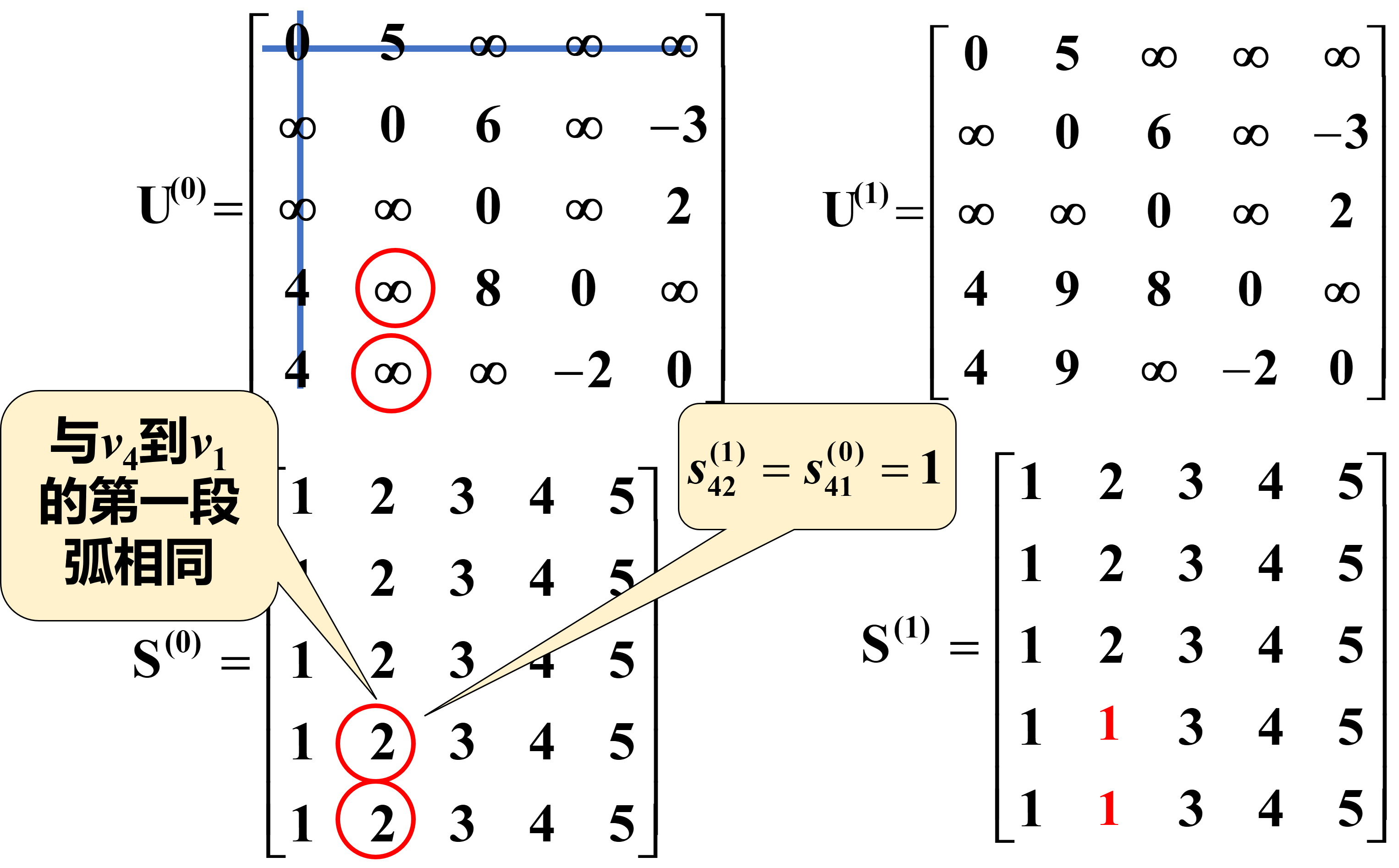
用U(1)的第二行、第二列修正其余的uij

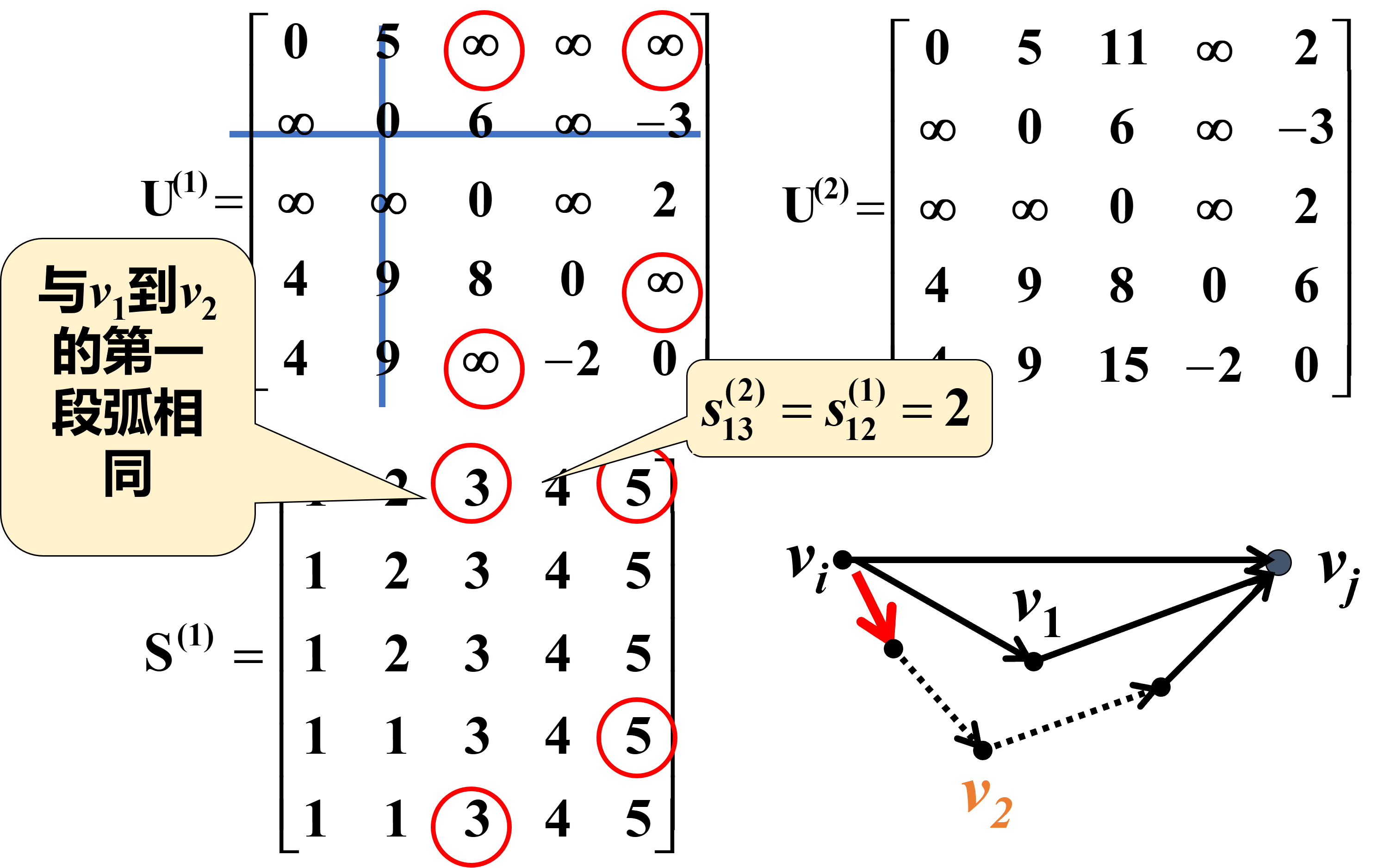
修正后，两点间路径可能经过v1和v2，如v1→v3的路径变为v1→v2→v3，其第一段弧与v1→v2的第一段弧相同。

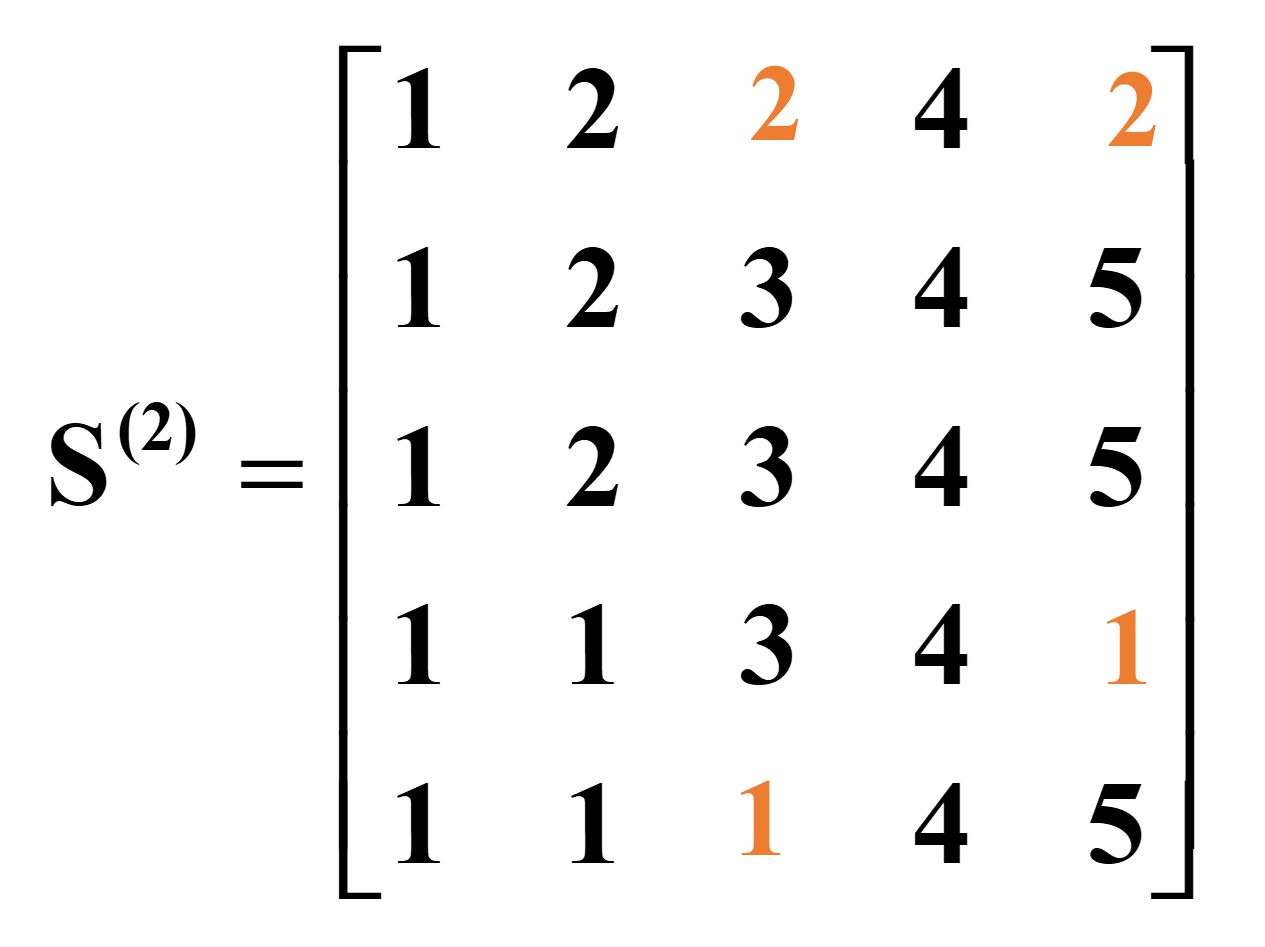
用U(2)第三行、第三列修正其余的uij

用U(3)第四行、第四列修正其余的uij

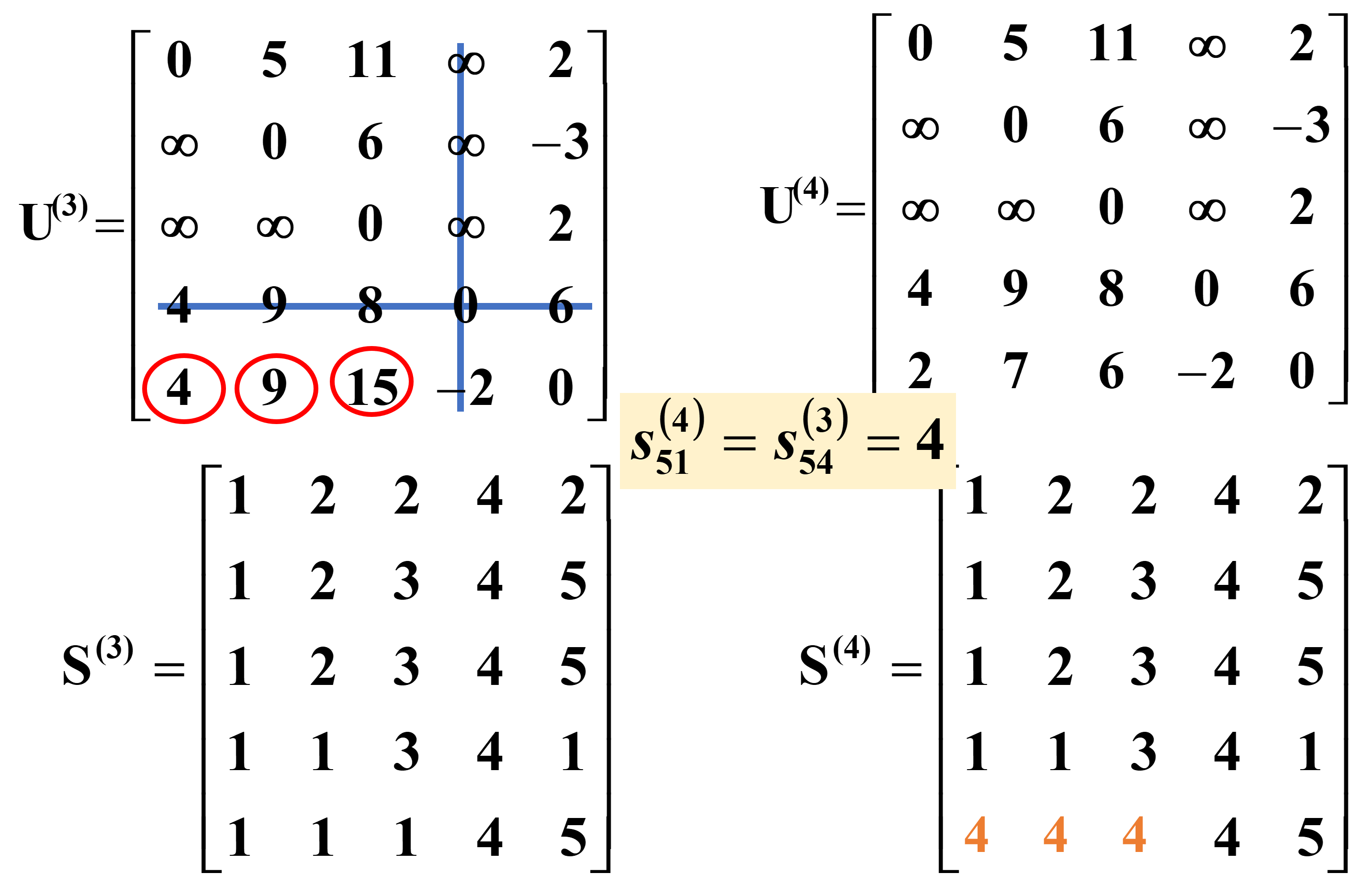
用U(4)第五行、第五列修正其余的uij

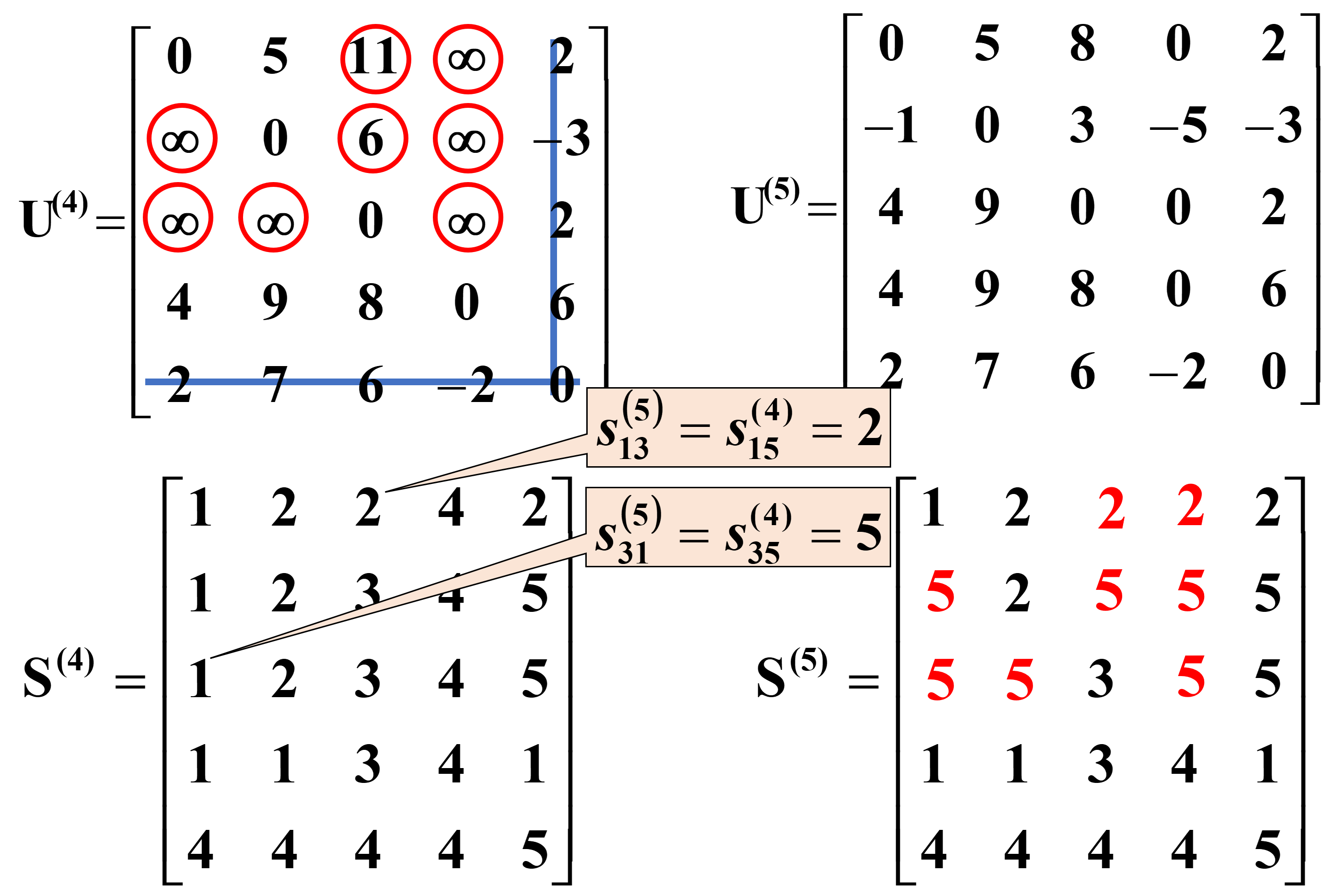
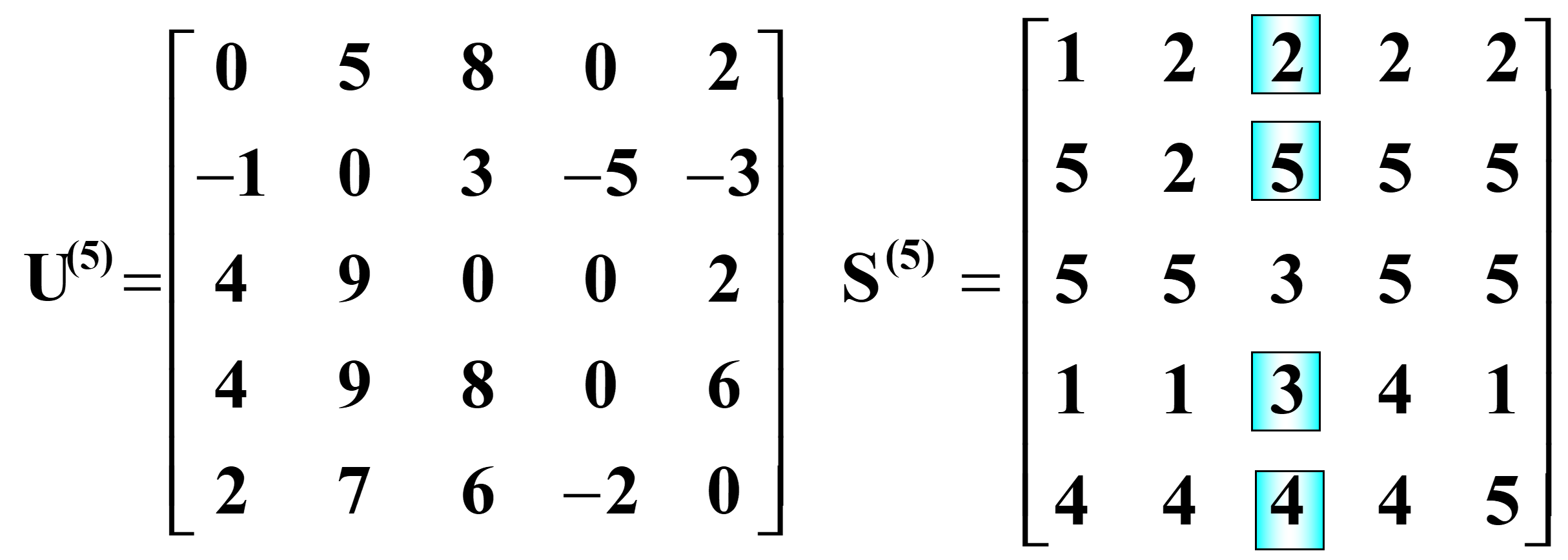
➡从v1到v3的最短路长度u13(5)=8

路径：∵ s13(5)=2,s23(5)=5,s53(5)=4,s43(5)=3

∴v1到v3的最短路路径为：P13=P(v1,v2,v5,v4,v3)

➡从v5到v2的最短路长度u52(5)=7

路径：∵ s52(5)=4,s42(5)=1,s12(5)=2

∴v5到v2的最短路路径为：P52=P(v5,v4,v1,v2)

★Dijkstra和Floyd方法对比

相同点

✔Dijkstra和Floyd都可以找到从一点到另一点的最短路径；

✔两者思路相似，都是每次增加一个跳板，然后更新两节点间距离。

不同点

✔Dijkstra是解决单源最短路径，而Floyd能解决任意源最短路径问题。但用Dijkstra算法依次改变起点的办法，也可计算任意源的最短路径；

✔Dijkstra属于贪心算法，通过选择将问题归为小的子问题，而贪心算法选择的策略具有无后效性，不存在回溯的过程，因此不能计算负权图。Floyd是动态规划思想，将大规模的问题自顶向下划分为了小规模的问题，因为动态规划是可以回溯的，所以它可以计算负权图。

以上就是关于最短路问题的全部内容了，学习完这一节，大家可以试着对一些实际问题进行应用练习。下一次小编将带大家学习最大流问题，敬请关注！