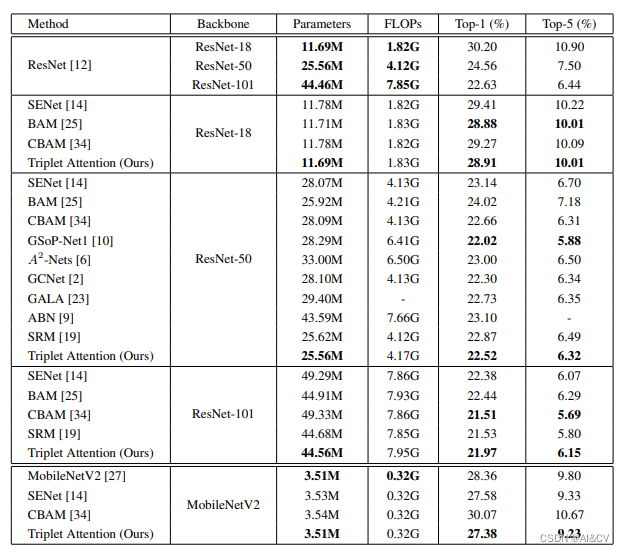
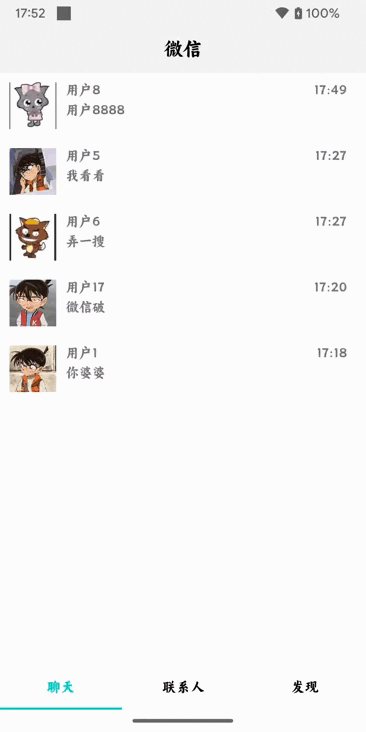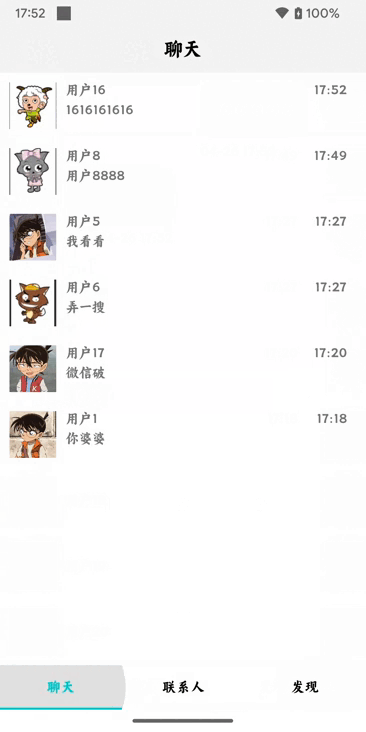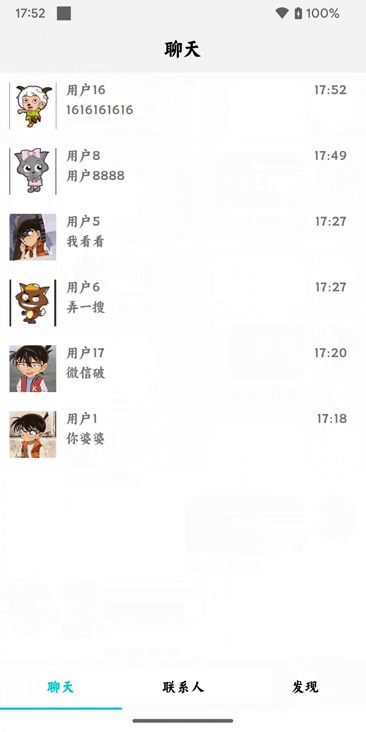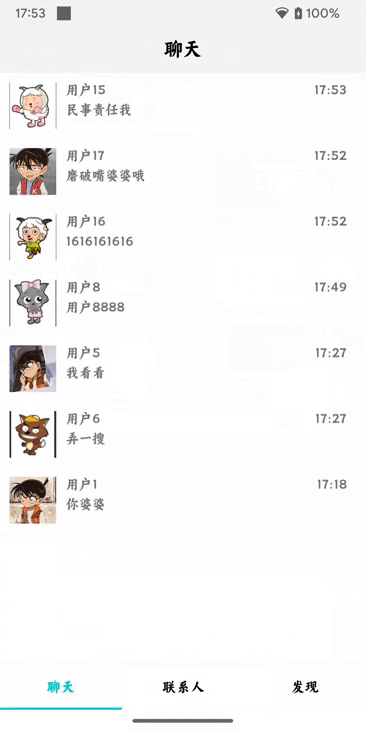
这里介绍两种代码中位运算非常常用的操作
n的二进制表示中第k位数——右移操作 + &1
例如说,我们需要计算11的第2位数。
11 = (1011)2
我们常规思路就是将其转化为二进制数后,直接观察对应位置的值
这里需要注意的是第k位数指的是从右开始的第k位,即个位数是第一位
但是数字在计算机中都是直接以二进制数存放的,所以并不需要像我们一样转化为二进制。
为方便处理,我们的处理方式就是
- 先将数字右移k位,让其位于第一位
- 之后
&1,就可以拿到第一位的值了
表示在代码中就是
n >> k & 1
例如我们现在需要输入n = 11的二进制的每一位
int n = 11; for(int k = 3 ; k >= 0 ; k -- ) cout << ( n >> k & 1) << " " ;输出的结果
也就是说,当n=11=(1011)2时
- 右移一位时,
n = 011 - 右移两位时,
n = 11 - 右移三位时,
n = 1
二进制1的个数——lowbit操作
lowbit:返回x的最后一位1例如,x = 1100 ,lowbit(x) = 100
实现方式:
x & -x
问题一;为什么可以返回最后一位呢?
-x在计算机中是以补码存放的,也就是说
-x = ~x + 1拿一个具体样例来说
加上1之后,前面都将&0,结果直接是0
因此,就能得到X的最后一位1
我们只需要减去对应的lowbit就可以将最后的一位1给删除,一个个删除后,当x=0时,表示当前已经没有1了
实现代码:
#include<iostream>
using namespace std;
int lowbit(int x){
return x & -x;
}
int n , x;
int main(){
scanf("%d" , &n);
while(n --){
int cnt = 0;
scanf("%d" , &x);
int res = 0;
while(x){
x -= lowbit(x);
cnt ++;
}
cout << cnt << " ";
}
return 0;
}
问题二:为什么减去lowbit就可以删去1呢?
这个问题,我们需要从计算机组成原理角度来讲解。
在计算机中并没有减法操作,且每一个数在计算机中都表示为二进制
因此,当需要运行减法操作时,实际上运算的是:x + (~y)
当我们需要计算这样一个数
x = 1010 1000,对应lowbit = x & -x =0000 1000
当他们x - lowbit(x) ,即x & (~lowbit(x))
仔细验算一遍的确是减去了最后一个1
当然也可以带入十进制运算
- X:168
- lowbit(x):8
x - lowbit = 160
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RkozuHQz-1682513371874)(assets/image-20230426202121-e9bd0e8.png)]](https://img-blog.csdnimg.cn/5b086ad6969d49b1992a7792b256c5e2.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vGArc1kt-1682513371874)(assets/image-20230426203011-oa8upnc.png)]](https://img-blog.csdnimg.cn/20880cfc5301451ab7160a731caa7dd5.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IdrT10wI-1682513371875)(assets/image-20230426203159-j0funy8.png)]](https://img-blog.csdnimg.cn/45af911d276a49aaa7e63ae07104e0ce.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YEhylgck-1682513371875)(assets/image-20230426204003-wd19egw.png)]](https://img-blog.csdnimg.cn/d2fc7add13004a669bf7c88be9af6647.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-53fjjvWY-1682513371875)(assets/image-20230426204815-uyz9q3b.png)]](https://img-blog.csdnimg.cn/37577bf1dad445859fd3e672bf973546.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vEEZCuJ7-1682513371876)(assets/image-20230426204856-t3auerh.png)]](https://img-blog.csdnimg.cn/d2de342b74614975bfe059cf244f7e58.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zBVZEaDe-1682513371876)(assets/image-20230426204911-a4ruytq.png)]](https://img-blog.csdnimg.cn/eabe304ba89748de9e697c06e7647ac9.png)