来源书籍：

TENSORFLOW REINFORCEMENT LEARNING QUICK START GUIDE

《TensorFlow强化学习快速入门指南-使用Python动手搭建自学习的智能体》

著者：[美]考希克·巴拉克里希南（Kaushik Balakrishnan）

译者：赵卫东

出版社：Packt 机械工业出版社

1.Double DQN、竞争网络结构和Rainbow

1.1 了解Double DQN

1.2 理解竞争网络结构

1.3 了解Rainbow网络

1.3.1 先验经验重放

1.3.2 多步骤学习

1.3.3 分布式强化学习

1.3.4 噪声网络

2.思考题

1.Double DQN、竞争网络结构和Rainbow

第 3 章讨论了深度 Q 网络 (DQN) 算法, 以及如何用 Python 和 TensorFlow 实现, 并训练它来玩 Atari Breakout 游戏。在 DQN 中, 使用相同的Q网络来选择和评估一个动作。这会高估 Q 值，导致过度乐观的估计值。为了缓解这种情况, DeepMind 发表了另一篇论文，提出了分离动作选择和动作评估的想法。这是 Double DQN ( DDQN) 架构的关键，将在本章中进行研究。

之后, DeepMind 发表了另一篇论文, 提出包含两个输出值的 Q 网络架构, 一个代表价值函数 𝑉(𝑠), 另一个是在给定状态下采取行动的优势函数 𝐴(𝑠,𝑎) 。Deep-Mind 将这两者组合起来计算 𝑄(𝑠,𝑎) 动作值, 而不是像 DQN 和 DDQN 那样, 直接确定它的取值。这些 Q 网络架构被称为竞争网络结构，因为此时神经网络具有双输出值 𝑉(𝑠) 和 𝐴(𝑠,𝑎), 随后被组合以获得 𝑄(𝑠,𝑎) 。本章将学习这些双重网络。

本章中学习的另一个扩展网络是 Rainbow 网络, 它是几种不同想法融合的一个混合算法。

1.1 了解Double DQN

DDQN 是 DQN 的扩展，在贝尔曼更新中使用目标网络。具体来说，在 DDQN 中, 贪婪最大化主要网络的 Q 函数来评估目标网络的 Q 函数。首先, 使用 vanilla DQN 目标进行贝尔曼方程更新。然后, 扩展到 DDQN 以进行相同的贝尔曼方程更新, 这是 DDQN 算法的关键。之后, 在 TensorFlow 中编写 DDQN 代码来玩 Atari Breakout 游戏。最后，对比 DQN 和 DDQN 两种算法。

更新贝尔曼方程在vanilla DQN 中，贝尔曼更新的目标如下：

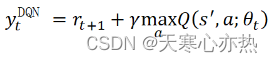
$\theta _{t}$ 表示目标网络的模型参数。上式会导致 Q 函数的过度预测, 因此更改 DDQN ，将目标值 $y_{t}$ 替换为:

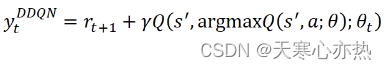
必须区分 Q 网络参数 𝜃 和目标网络模型参数 $\theta _{t}$ 。

1.2 理解竞争网络结构

在 DQN 和 DDQN 以及文献中的其他 DQN 变体中, 重点主要是算法, 即如何高效、稳定地更新价值函数神经网络。尽管这对于开发鲁棒的强化学习算法至关重要，但推动该领域发展的一个相似但互补的方向是创新和开发适合无模型强化学习的新型神经网络结构。这正是竞争网络结构背后的概念, 也是 DeepMind 的另一个贡献。

竞争网络结构中包含的步骤如下:

1）竟争网络结构; 与标准的 DQN 作比较。

2）计算 𝑄(𝑠,𝑎) 。

3）从优势函数中减去优势的平均值。

由前文可知, DQN 中 Q 网络的输出是 𝑄(𝑠,𝑎), 即行为 - 价值函数。在竞争网络中, Q 网络有两个输出值: 状态价值函数 𝑉(𝑠) 和优势函数 𝐴(𝑠,𝑎) 。可以将它们结合起来计算状态 - 动作价值函数 𝑄(𝑠,𝑎) 。这样做的好处是网络不需要学习每个状态下每个动作的价值函数, 这在行为不影响环境的状态下尤其有用。

如果一辆汽车在笔直的没有其他车辆的公路上行驶, 那么不需要做出任何行为, 在这种状态下使用 𝑉(𝑠) 就足够了。但如果道路突然出现了弯道或其他车辆进人汽车的附近, 就需要采取措施。因此, 在这些状态下, 优势函数开始发挥作用, 以找到给定的行动可以提供超过状态价值函数的递增收益。这是通过使用两个不同的分支将同一网络中的 𝑉(𝑠) 和 𝐴(𝑠,𝑎) 的估计分离, 然后将它们组合在一起。

标准DQN网络和竞争网络结构如图所示。

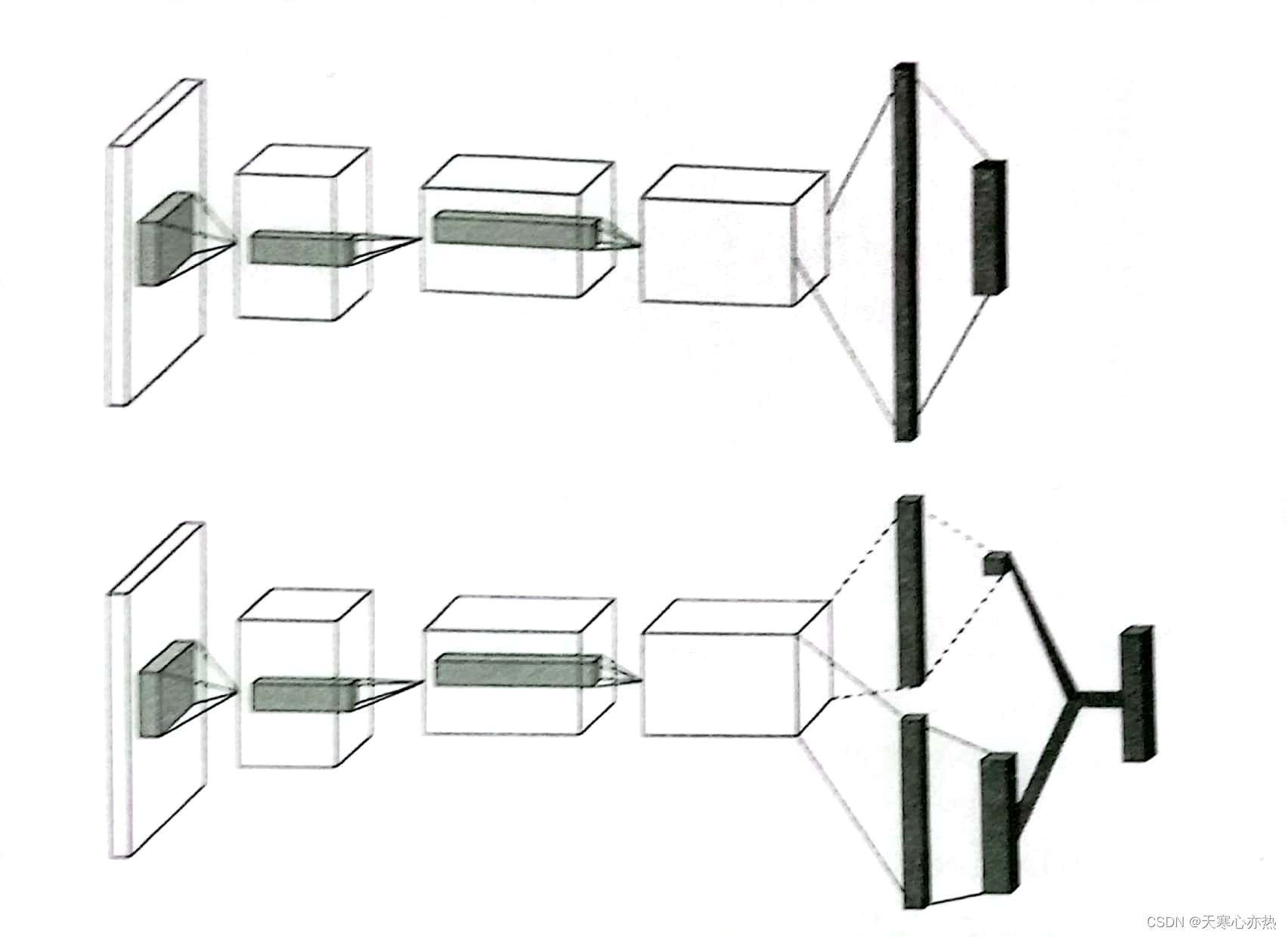
标准DQN网络（上）和竞争网络结构（下）

可以通过下面的公式计算动作 - 价值函数 𝑄(𝑠,𝑎) :

𝑄(𝑠,𝑎)=𝑉(𝑠)+𝐴(𝑠,𝑎)

然而, 这并不是唯一的, 因为可以用 𝑉(𝑠) 来预测一个量 𝛿, 而用 𝐴(𝑠,𝑎) 来预测同样的量 𝛿 ，这使得神经网络预测无法识别。为了避免这个问题，竞争网络论文的作者建议采用以下方法将 𝑉(𝑠) 和𝐴(𝑠,𝑎) 结合起来:

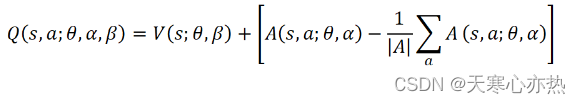
式中, |𝐴| 表示动作数, 𝜃 表示 𝑉(𝑠) 和 𝐴(𝑠,𝑎) 流之间共享的神经网络参数; 此外, 𝛼 和 𝛽 用于表示两个不同流 (即 𝐴(𝑠,𝑔) 流和 𝑉(𝑠) 流) 中的神经网络参数。从本质上讲, 在前面的方程中, 从优势函数值中减去平均优势函数值, 然后将与状态价值函数求和, 得到 𝑄(𝑠,𝑎) 。竞争网络结构论文的链接为 https://arxiv.org/abs/1511.06581。

1.3 了解Rainbow网络

下面介绍 Rainbow 网络, 这是几个不同 DQN 改进的集合。自有关 DQN 的论文问世以来, 出现了几种不同的改进方案, 取得了显著的成功。这促使 DeepMind 将几个不同的改进方案组合成一个集成 agent, 称之为 Rainbow DQN 。具体来说, 六种不同的 DQN 改进组合成一种集成的 Rainbow DQN agent。这六项改进概括如下:

- DDQN

- 竞争网络结构

- 先验经验重放

- 多步聚学习

- 分布式强化学习

- 噪声网络

DQN改进
前文已经介绍了DDQN 和竞争网络结构, 并用 TensorFlow 对它们进行了编码, 其余的改进将在下面描述。

1.3.1 先验经验重放

对于一个重放缓冲区, 其中所有的样本都具有相同的被采样概率。然而, 这并不是非常有效, 因为有些样本比其他样本更重要。这就是为什么需要先验经验重放, 其中具有更高时间差 (TD) 误差的样本以比其他样本更高的概率进行采样。第一次将样本添加到重放缓冲区时, 将设置最大优先级值, 以确保缓冲区中的所有样本至少采样一次。此后, TD 误差用于确定要采样的经验概率, 计算公式如下:

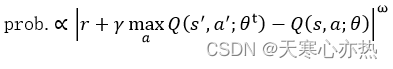
式中, r 是奖励; θ 是主要的 Q 网络模型参数; $\theta ^{t}$ 是目标网络参数; ω 是一个确定分布形状的正超参数。

1.3.2 多步骤学习

在 Q-learning 中, 积累一个单个奖励, 并在下一步使用贪婪操作。也可以使用多步目标, 并从单个状态计算一个 n 步返回:

n步返回的值 $r_{t}^{n}$ 在 Bellman 的更新中使用, 可以更快地学习。

1.3.3 分布式强化学习

在分布式强化学习中涉及收益的近似分布, 而不是期望收益。由于在数学上比较复杂, 超出了本书的范围, 在此不做进一步讨论。

1.3.4 噪声网络

在某些游戏中 (例如 Montezuma's revenge ), $\varepsilon$ -greedy 并不奏效, 因为在收到第一个奖励之前, 需要执行许多动作。在此设置下, 建议使用结合确定性流和噪声流的噪声线性层:

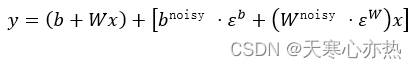
式中, x是输入; y是输出; b 和 W 是确定性流中的偏置和权重; $b^{noisy}$ 和 $W^{noisy}$ 分别是噪声流中的偏置和权重; $\varepsilon ^{b}$ 和 $\varepsilon ^{W}$ 是随机变量, 与偏置和权重做点乘。在噪声流中, 网络可以选择忽略状态空间某些区域中的噪声流并根据需要使用, 这就允许使用状态确定的探索策略。
本书不会对完整的 Rainbow DQN 进行编码, 因为其过于繁杂。作为替代, 我们可以使用一个名为 Dopamine 的开源框架来训练 Rainbow DQN agent。

2.思考题

（1）为什么DDQN比DQN性能更好？

答：DQN 高估了动作 - 价值函数 Q(s,a) 。为了解决这个问题, 引入了 DDQN 。DDQN 表现得比 DQN 好。

（2）竞争网络结构在训练中如何起作用？

竞争网络结构的优势函数和状态价值函数有单独的流, 将它们组合以获得 Q(s,a) 。这种分支再组合的做法可以更稳定地训练 RL agent。

（3）为什么先验经验重放会加速训练？

先验经验重放 (PER) 更重视 agent 性能不佳的体验样本, 因此与 agent 表现良好的其他样本相比, 这些样本的采样频率更高。通过频繁使用 agent 表现不佳的样本, agent 能够时常地处理其弱点, 因此 PER 可以加快训练速度。

（4）粘性行为在训练中有何帮助？

在一些计算机游戏中, 例如 Atari Breakout, 模拟器每秒的帧数太多了。如果每个时间步长从策略中对单独的操作进行采样, 那么 agent 的状态可能在一个时间步长中不会改变, 因为它太小。因此, 当相同的动作在有限但固定数量的时间步长 ( 例如 n) 上重复时, 使用粘性行为, 并且在这 n 个时间步长累积的总奖励被用作所执行动作的奖励。在这 n 个时间步长中, agent 的状态已经发生相当大的变化, 足够评估所采取动作的效力。n 太小会阻碍 agent 学习好的策略, 太大也可能产生问题。必须选择执行相同操作的正确时间步长, 这取决于所使用的模拟器。