1. 介绍

骨架 skeleton

骨架的定义：就是目标的前景像素点集合内部最大的内切圆盘，将所有的内切圆盘的圆心连起来就是骨架

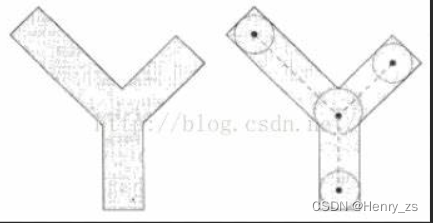
一个骨架的区域就是这个区域中与区域边界等距的集合，

骨架的实现可以参考这篇文章：形态学 - 骨架和形态学 - 细化

中轴变换 Medial axis transformation

中轴变换可以计算前景区域的中轴，一个区域的骨架就定义为这个区域的中轴

它的中轴定义如下：R 是前景区域， B 是前景区域的边界。如果前景区域 R 中的每个点p，在边界B中找到最近的点。如果这个最近的点不是唯一的，那么点p定义为前景区域R的中轴

骨架其实就是物品最中间的那根轴，因此这个轴到周围边界的距离应该是相等的

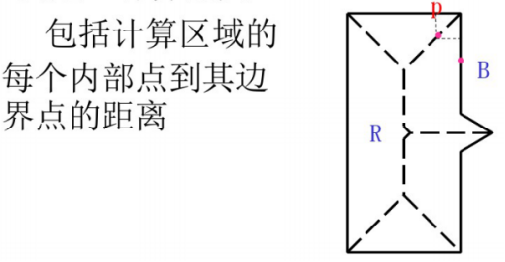
查看源图像

中轴的概念可以用 '草原大火' 的概念去理解：

把图像处理成二值图像，在前景区域的边界处点火
火焰会以同样的速度向前景区域蔓延，
那么中轴就是火焰接触的集合

距离变换 distance transform

中轴变换需要计算大量的点到边界的距离，可以通过距离变换去代替

距离变换的意思是，对于一副二值图像而言。前景区域（非0）到最近的背景区域（0值）的距离

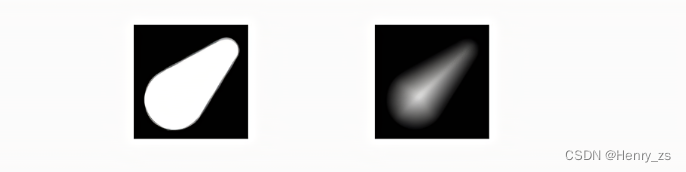
因此，距离变换后的图像是一副灰度图像，灰度值的大小与前景像素点距离背景区域的远近成正相关。也就是说，图像越亮--->灰度值越大--->距离背景越远，那么骨架就是定义为距离变换后的局部极大值的区域

这里书上的介绍是 '脊' ，也就是局部极大值的集合。因为没有介绍局部极大值的范围，下面代码的实现是 4邻域

2. 距离变换的代码实现

因为形态学的骨架提取之前已经介绍过了，这里不再介绍

而中轴变换等效于距离变换，因此这里只介绍距离变换的代码

如上述代码，首先将图像进行 OTSU 二值化，然后对二值图像进行距离变换

distanceTransform 函数介绍

第二个参数计算距离的方法，常用的有下面几种

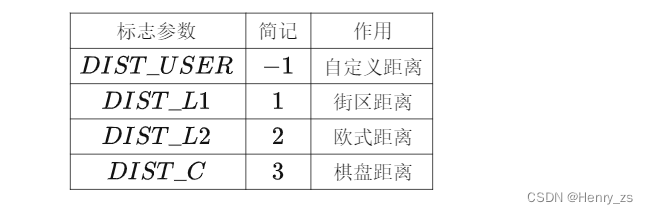
第三个参数为 maskSize：距离变换掩码矩阵的大小

当选择使用街区距离时，掩码尺寸选择3×3还是5×5对计算结果都没有影响，因此为了加快函数运算速度，默认选择掩码尺寸为3×3
当选择欧式距离时，掩码尺寸为3×3时是粗略的计算两个像素之间的距离，而当掩码尺寸为5×5时是精确的计算两个像素之间的距离，精确计算与粗略计算两者之间存在着较大的差异，因此在使用欧式距离时推荐使用5×5掩码
当选择棋盘距离时，掩码的尺寸对计算结果也没有影响，因此可以随意选择

normalize 函数介绍

因为图像的返回是浮点型的数据或者灰度值往往不大，是一副几乎全黑的图像，因此这里对图像进行了放缩 normalize

这里只对下面这串代码介绍：

img_dst = cv2.normalize(img_dst, None, 0, 255, norm_type=cv2.NORM_MINMAX, dtype=cv2.CV_8U)

0，255 代表缩放后图像的灰度值在 0-255之间

cv2.NORM_MINMAX 代表：

取局部最大值

距离变换后，取最大值的代码为

其实就是二维矩阵求取局部最大值，但是需要注意的是，我们是不对背景区域求取局部极值的

注：这里局部的范围是 4邻域

完整代码

import cv2
import numpy as np


def local_maximum(x):   # 取局部最大值

    dst = np.zeros(x.shape, dtype=np.uint8)     # 处理的结果
    height,width = x.shape[:2]

    for i in range(1, height - 1):
        for j in range(1, width - 1):
            if x[i][j] != 0:
                if (x[i][j] >= x[i - 1][j]) and (x[i][j] >= x[i + 1][j]) and (x[i][j] >= x[i][j - 1]) and (x[i][j] >= x[i][j + 1]):
                    dst[i][j] = 255
    return dst


img = cv2.imread('./img.jpg',0)
_, img_bin = cv2.threshold(img,0,255,cv2.THRESH_OTSU+cv2.THRESH_BINARY)         # 二值化图像

img_dst = cv2.distanceTransform(img_bin,cv2.DIST_L2,5)                              # 距离变换
img_dst = cv2.normalize(img_dst, None, 0, 255, norm_type=cv2.NORM_MINMAX, dtype=cv2.CV_8U)  # 归一化,为了方便显示

ret = local_maximum(img_dst)            # 取距离变换后的局部最大值

cv2.imshow('img',np.hstack((img_bin,img_dst,ret)))
cv2.waitKey()
cv2.destroyAllWindows()

处理的结果为：二值图、距离变换图、骨架