随着深度学习的发展，基于单张RGB图像的人体三维重建取得了持续进展。

但基于现有的表示方法，如参数化模型、体素栅格、三角网格和隐式神经表示，难以构筑兼顾高质量结果和实时速度的系统。

针对上述问题，天津大学团队联合清华大学与英国卡迪夫大学在NIPS2022的工作中提出一种高效灵活的三维几何表示——傅里叶占有率场（FOF）。

 

 项目主页：http://cic.tju.edu.cn/faculty/likun/projects/FOF

代码链接：http://github.com/fengq1a0/FOF 

 

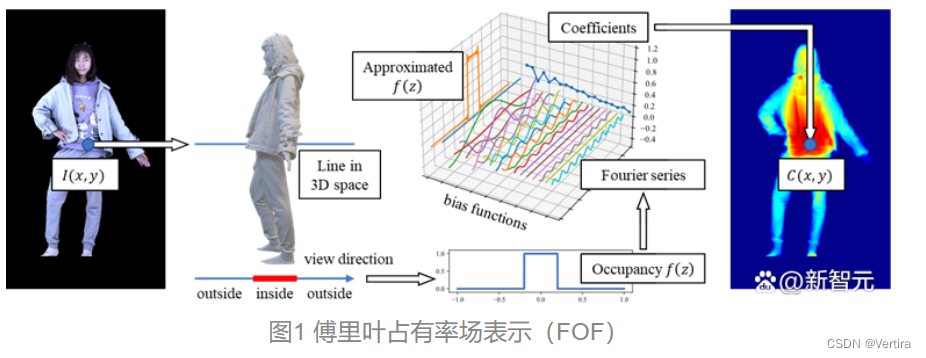
FOF将三维物体压缩为垂直于视线方向的二维向量场，离散化后可与二维卷积神经网络相兼容，从而跨越了三维几何与二维图像之间的鸿沟。

FOF非常灵活，可以高效地与三角网格相互转换。这使得人体参数化模型可以直接作为单目重建的几何先验，极大地提升了重建精度。

基于FOF，研究团队构建了第一个30+FPS的高质量实时单RGB相机的人体三维重建框架，推动了3DTV、全息会议等应用的发展。

作者还展示了基于FOF的单RGB相机人体三维重建（基线版本）的实时demo，旋转跳跃、抖腿都不在话下。

傅里叶占有率场

方法动机

现有单RGB相机人体重建方法大多以深度隐式表示为基础，此类方法需要在空间中采样大量的点，提取相应特征后交与MLP处理，从而获得对应点的占有率值。

这一过程极其耗时，同时可能产生不鲁棒的结果。

从整体上看，将特征向量与坐标作为MLP的输入，输出函数的值，这一过程实质上是使用特征向量表示相应的函数。

与神经网络相比，在赋范线性空间下使用广义傅里叶级数的系数向量对某一类函数进行近似表示是更为简单高效的方法。

以此为基本出发点，作者提出了一种全新三维表示——傅里叶占有率场（FOF）。

参考：

天大、清华提出基于单RGB相机的全新三维表示方法｜NeurIPS 2022 (baidu.com)