前置知识

维度灾难

内积的几何意义

向量与基向量的内积，就是向量在基向量方向上的投影坐标。

点乘（Dot Product）的结果是点积，又称数量积或标量积（Scalar Product）。在空间中有两个向量：

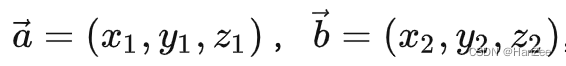
从代数角度看，点积是对两个向量对应位置上的值相乘再相加的操作，其结果即为点积。

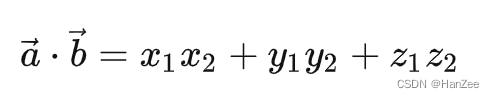
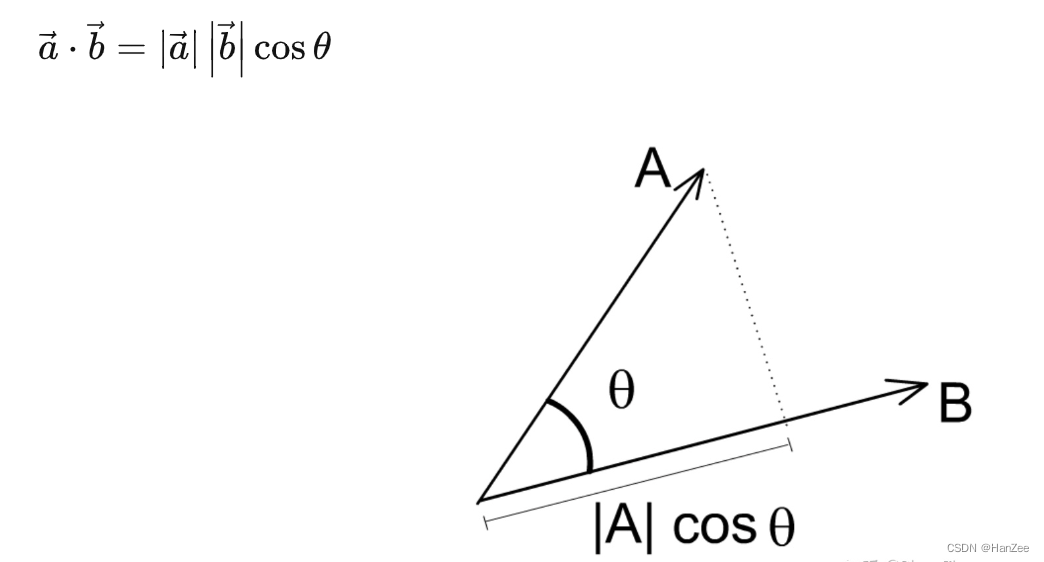
从几何角度看，点积是两个向量的长度与它们夹角余弦的积。

基

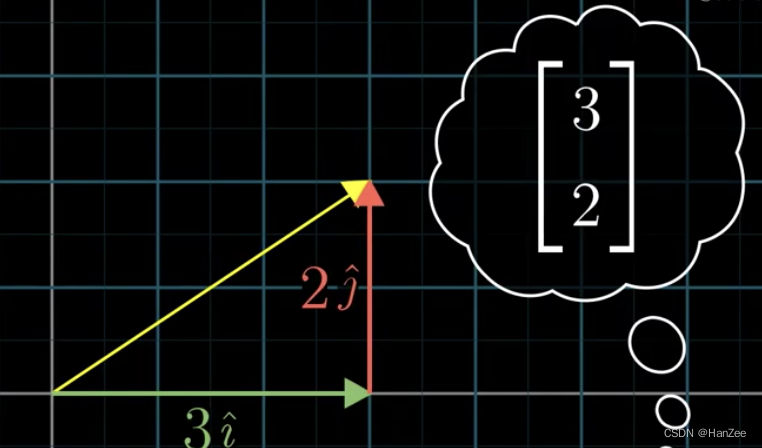
假设有一个列向量A：=[3,2]，如下图：

我们假设图中每个蓝色方格的单位为1，那么即使图中没有标注黄色向量是谁，我们也可以脱口而出他就是[3,2]。那么为什么我们可以直接看出他是谁呢？
答案也很简单，因为我们根据有一个参考依据，那就是坐标系（笛卡尔坐标系）。然而，这个二维坐标系他其实是由两个基向量：i ,j所组成的空间，其中：
$i=[1,0{]}^T,j=[0,1{]}^T$
我们可以把A看成在i向量扩大三倍，j扩大2倍，然后让他们作向量加法：

$$\begin{array}{r}\overrightarrow{A}=3\cdot \overrightarrow{i}+2\overrightarrow{j}=3\left[\begin{array}{c}1\\ 0\end{array}\right]+2\left[\begin{array}{c}0\\ 1\end{array}\right]\\ =\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}3\\ 2\end{array}\right]\\ =\left[\begin{array}{c}3\\ 2\end{array}\right]\end{array}$$

基变换

假设有两个人，小泽，小乐，他们看待问题的‘角度’不认同，也、也就是基不同，其中小泽的基向量为：

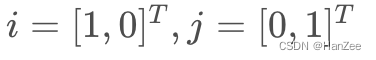
而小乐的基向量为为：b1 ,b2,b1b2这两个向量在小乐看来数值就是

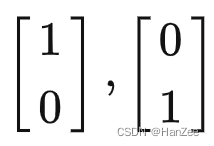
然而在小泽看来b1,b2数值为：

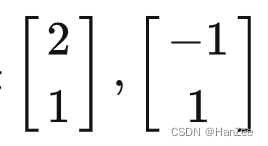
上面的向量A，在小泽的角度来看，就是[3,2]，然而在小乐的角度看就变成了：[5/3，1/3]。

它们之所以认为这个向量是不同的，因为它们看待问题的角度不同，‘横看成岭侧成峰，远近高低各不同’，也就是基向量不同。

不同基下的向量变换

假设小泽角度下的向量B：

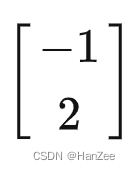
现在我们知道小泽与小乐的基向量，还知道了向量B在小泽中的数值表示，那么我们如果把小泽角度看的向量B，用小乐的角度表示，计算公式应该为：

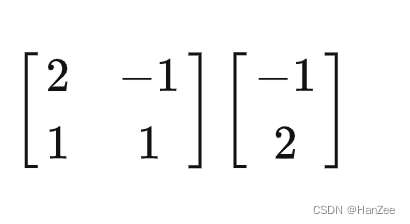
于是，我们就把小泽角度下的向量B，转换成了小乐角度的向量。

逆矩阵

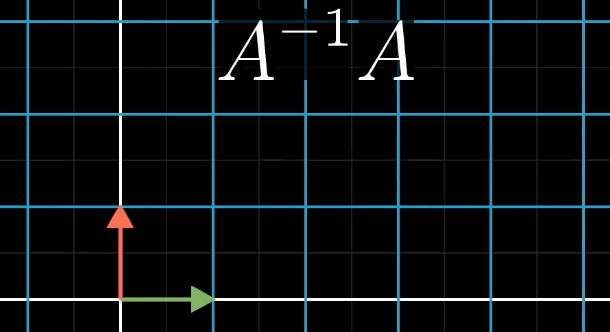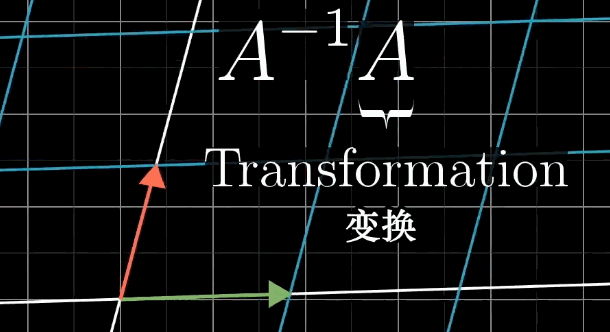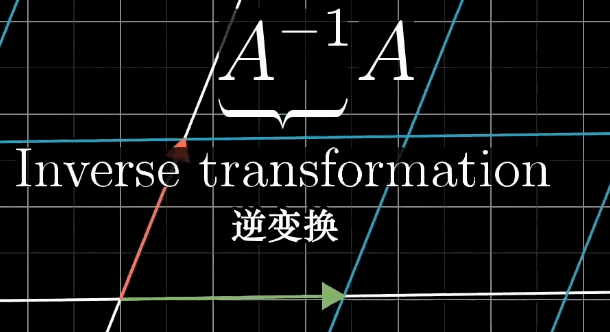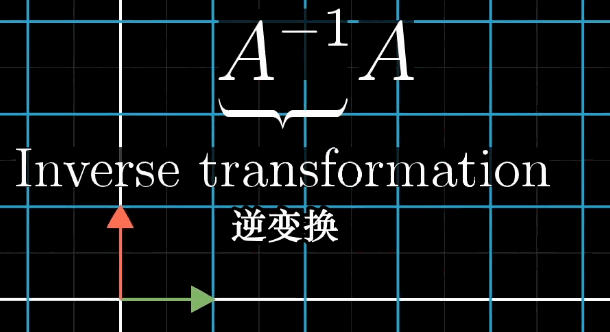
A的逆矩阵代表的含义就是A变换的逆过程。
求解 Ax =b的几何意义，就是找到一个向量x使得在A的变换下，x被映射为b。如果A为满秩矩阵，则有唯一解 $x=A^{-1}b$ ，也就是对b施加逆变换即可找到x。

在上面我们说在小泽的眼中，小乐的基向量b1,b2就是：

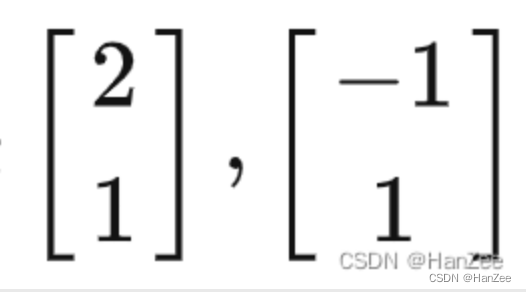
那么在小乐的眼中（以b1，b2为基向量），小泽的基向量i,j 如何表示呢？
这时候就用到了逆矩阵，把小泽的视角下的小乐的基向量的表示切换到小乐的视角小泽基向量的表示，需要用到上图矩阵做变换，那么我们反过来，就得到：

不同基下的空间变换

在上面我们已经介绍了什么是不同基下如何转换向量，下面我们介绍我们在不同基下的空间变换。
在小泽的视角中，我们如果想把坐标系逆时针旋转90度，如下图：

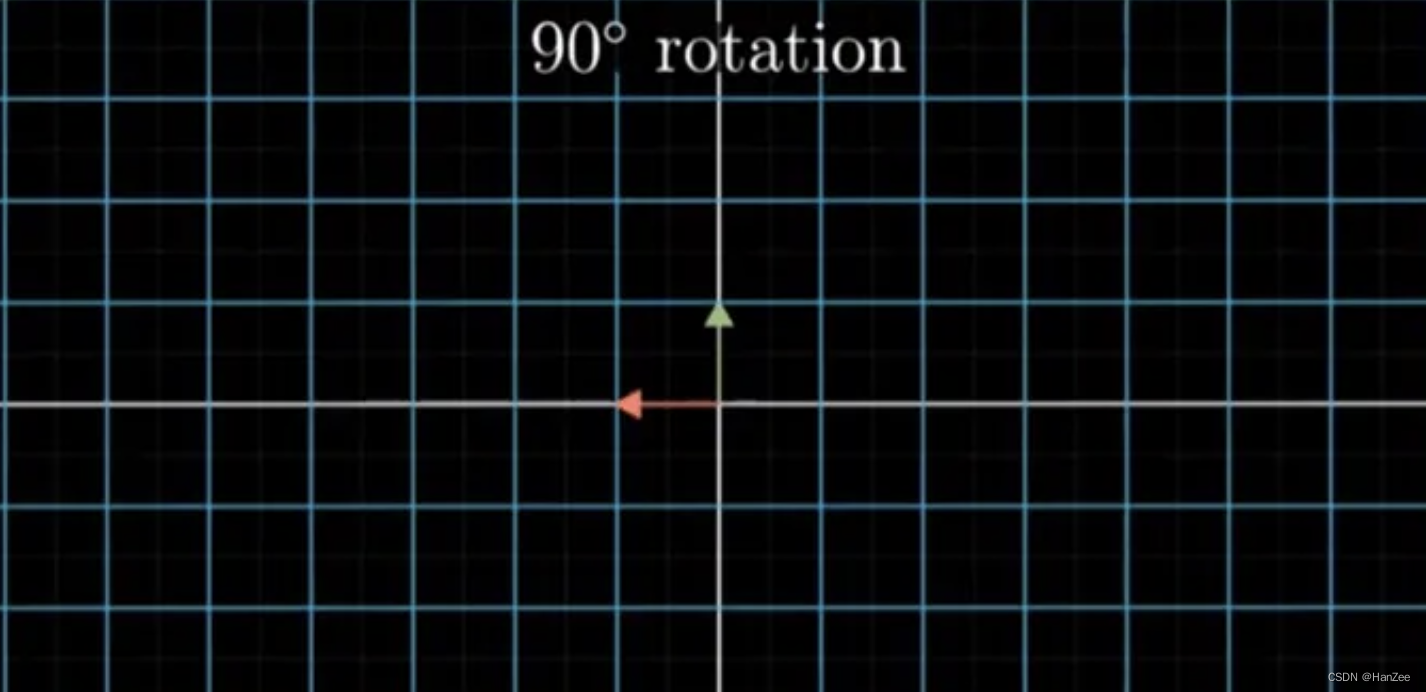
这个变换在小泽的视角下用矩阵A表示则是：

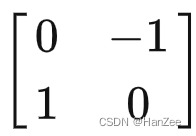
那么我们想做的就是知道：在小乐的视角下这个变换矩阵怎么表示呢？
现在我们已经有的是：二者的基向量，小泽的旋转矩阵。
我们的流程是：

1. 在小乐的视角下找到一组向量
2. 把这组向量用小泽的视角表示
3. 然后把这向量通过旋转矩阵得到旋转后的向量
4. 把旋转后的向量通过逆矩阵返回到小乐的视角

其中P为小乐视角下小泽基向量的表示，A为旋转矩阵，P的逆矩阵是小泽视角下小乐基向量的表示。

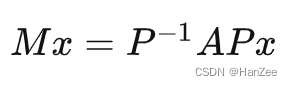
其中M就是我们要的小乐视角下的旋转矩阵，这就表示了不同基向量下的相同变换的相互转化。

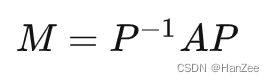
方差

方差多用于一维随机变量离散程度的表示，公式如下：

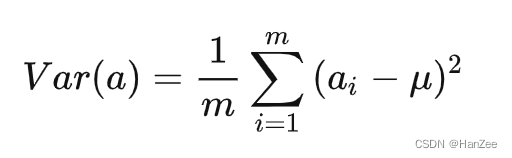
协方差

协方差是方差对两个以上随机变量的推广，它表示多个随机变量的联合变动程度，也叫相关性（正相关、负相关），当正相关协方差>0，负相关协方差<0,反之协方差=0。

1. 样例：

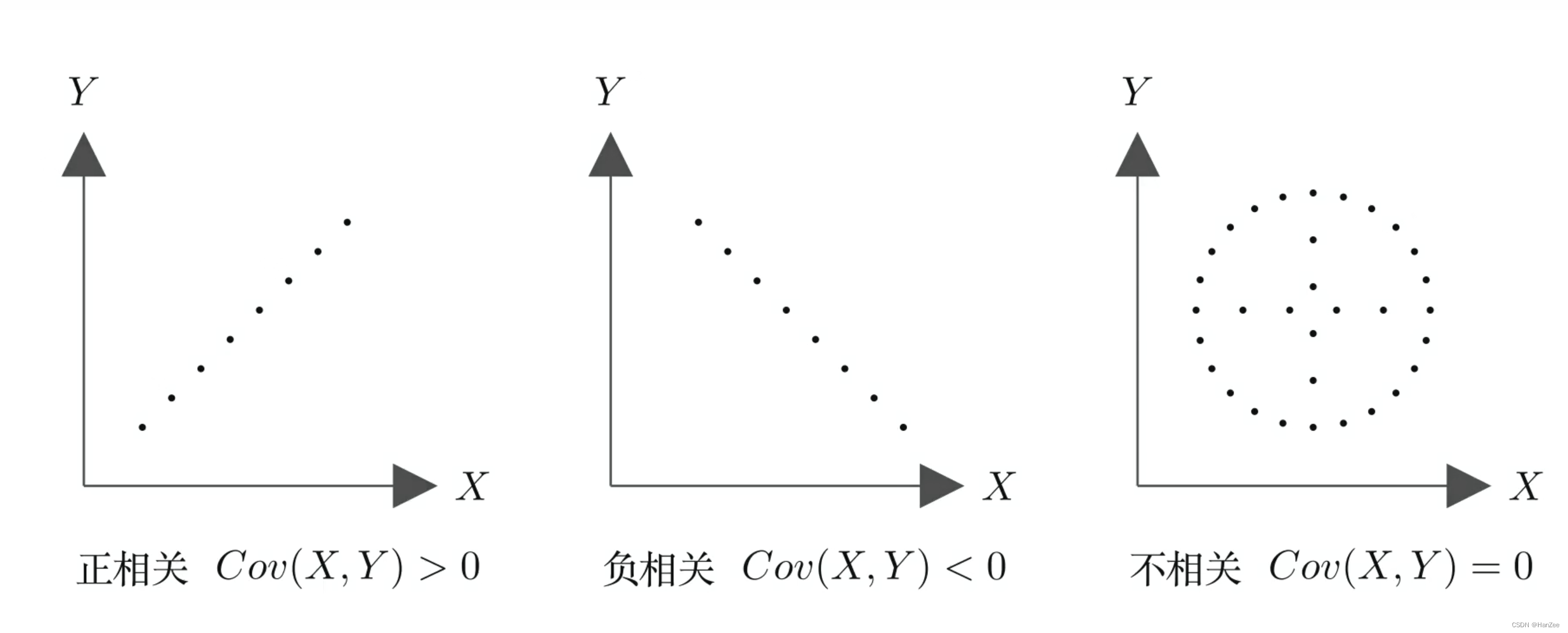
2. 公式：
   假设有两个随机变量a, b

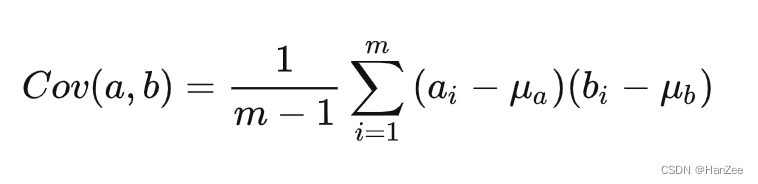
m-1为无偏估计，这个大家不必在意，当数据量足够大的时候，差距微乎其微。

协方差矩阵

假设有两个随机变量 a，b，观测数据矩阵用X表示。

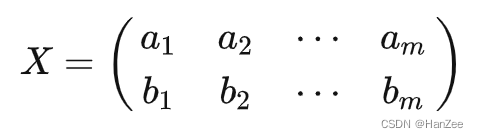
根据协方差表达式可知协方差矩阵的表达式（假设数据已经中心化）：

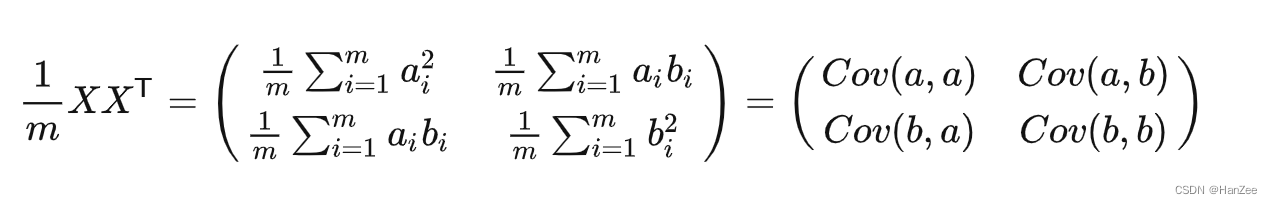
其中对角线上为每个随机变量的方差，其他为不同随机变量之间的协方差。

协方差矩阵对角化

通过观察协方差矩阵，我们发现协方差矩阵为实对称矩阵，所以可以对角化。

观测数据用X表示，它的协方差用C表示，旋转矩阵用P表示，旋转后的结果用Y表示，Y的协方差用D表示。

现在我们要通过P旋转矩阵X，那么旋转后的结果为：

根据上面的公式，Y的协方差D为：

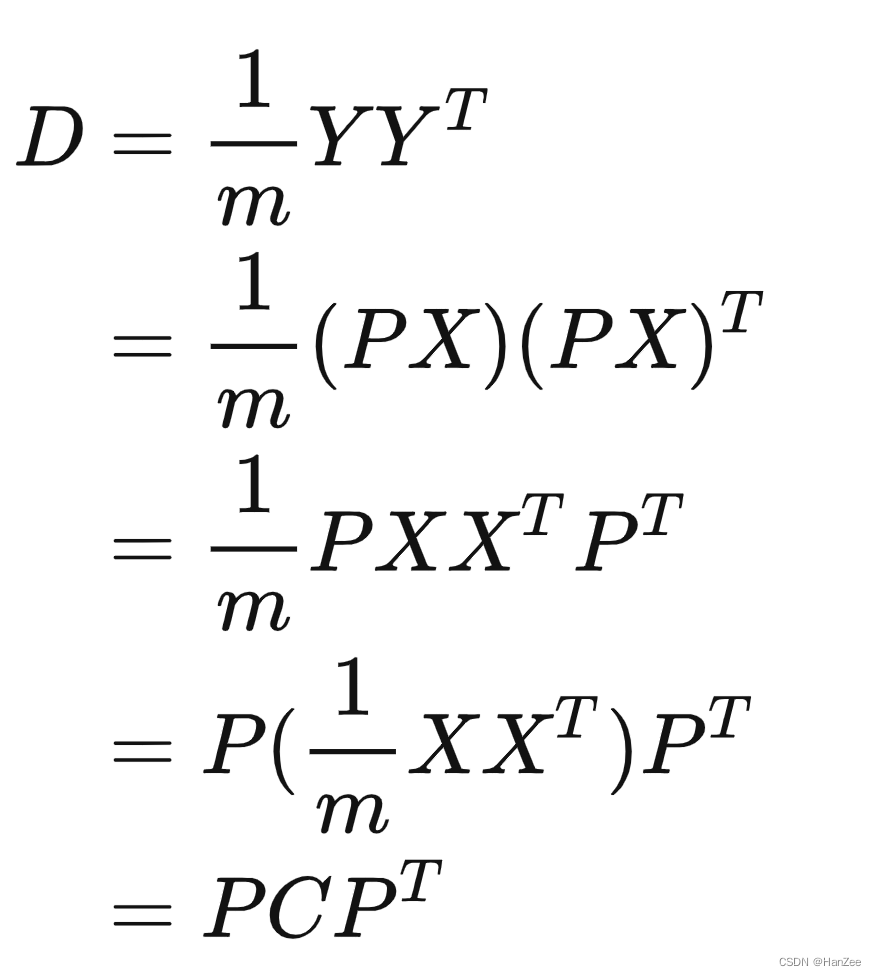
特征值分解、空间变换

主成分分析（PCA）

前面介绍了那么多的基础知识，下面我们来说一下PCA到底是在做一件什么事呢？
假设有一组二维数据：

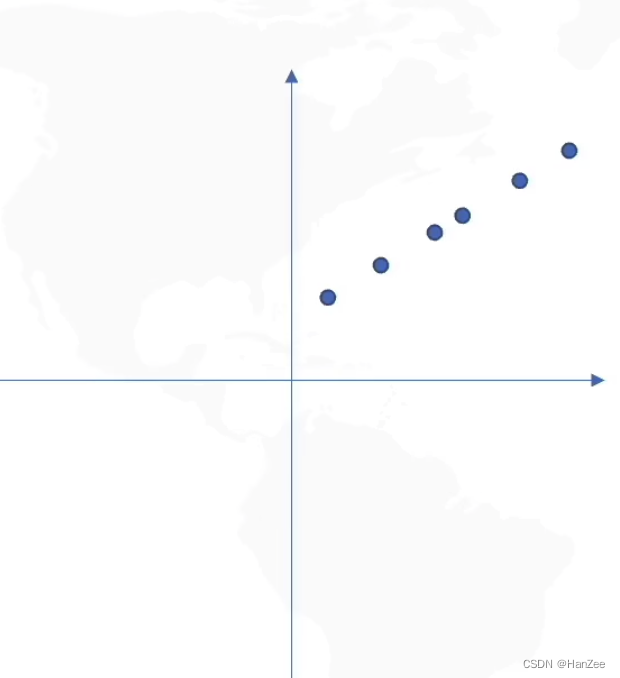
我们如果想找到其中一个点，就要用两个值表示，现在想对上面的数据降维，就拿一个数值来表示上面的点。

从基变换中我们了解到，同一个向量在不同的基坐标系下可以有不同的表示，但是他们本质是不变的，就如同‘你好这个词’，在中文下翻译为‘你好’，在英文下就是‘Hello’，但是他们本质的意思不变。

所以PCA在做的事情就是，找到一组新的的基坐标系，在这个坐标系里我们可以知道那个维度重要，这样我们就可以省略掉那些不重要的维度从而达到降维的目的。

也可以说是：将一组线性相关的变量，通过正交变换，变成线性无关，也就是原始特征空间的重构。

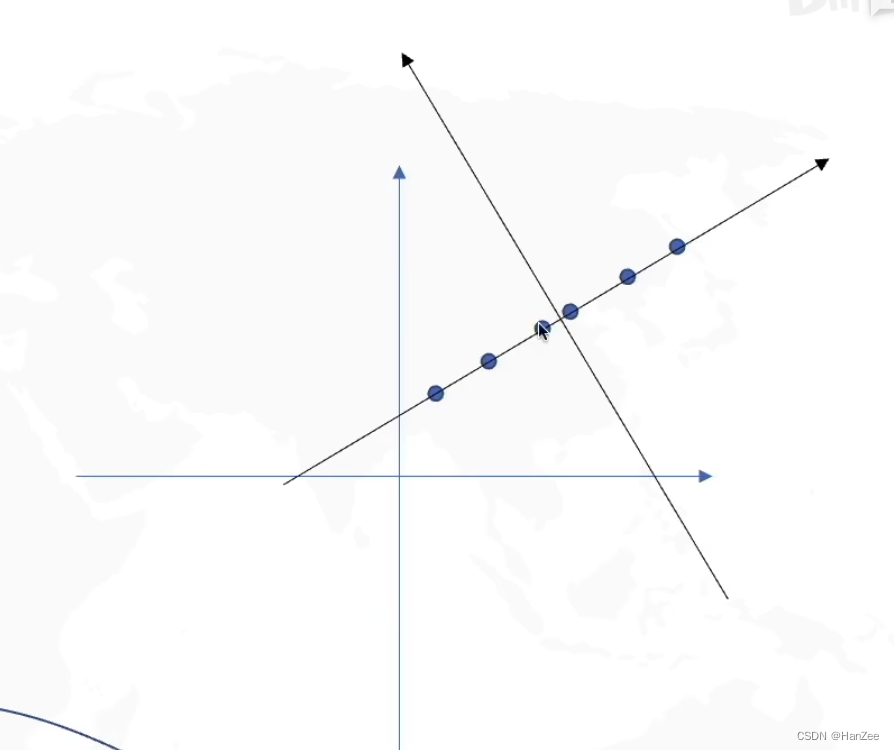
在实际的数据中，往往不像上面的图展示的那样，数据可以完美的在一个坐标轴中，实际的数据如下：

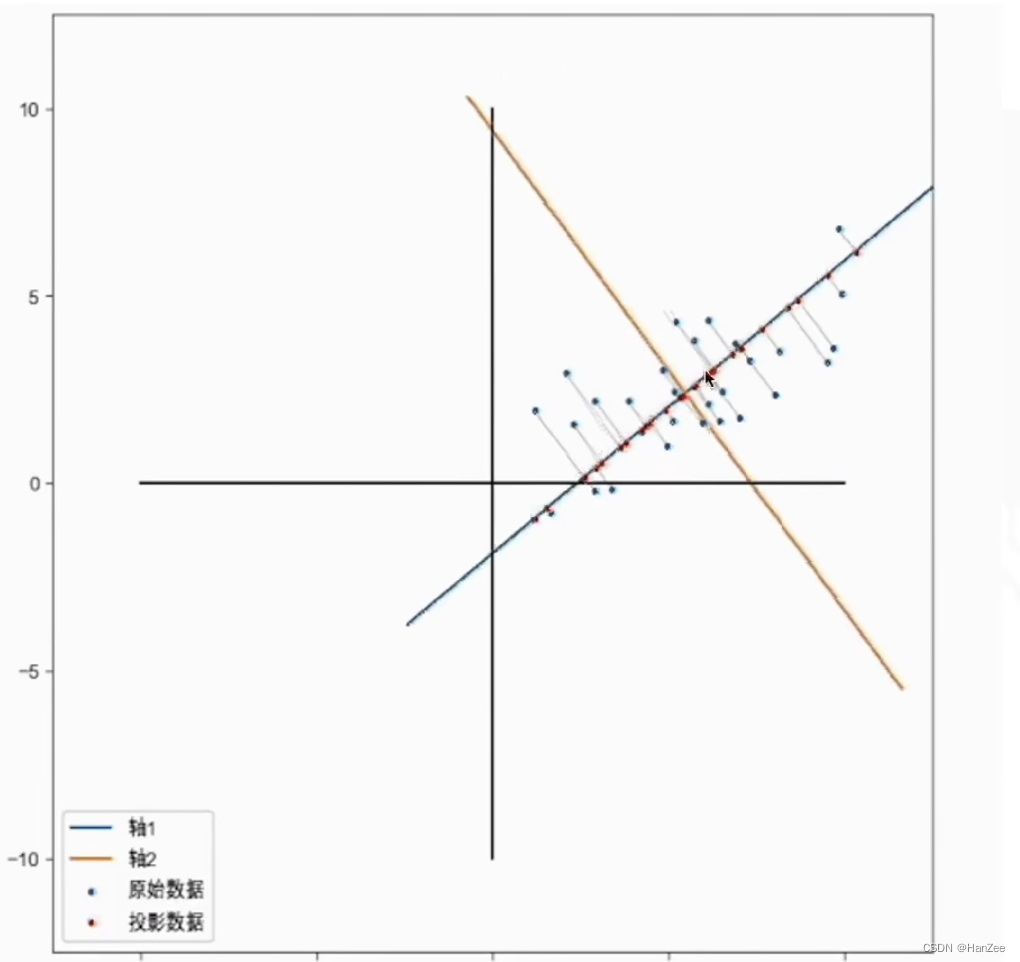
数据往往不会都呆在同一条直线上，我们如果找到了上面所描述的坐标系，然后在新的坐标系表示每一个点可能是这样：

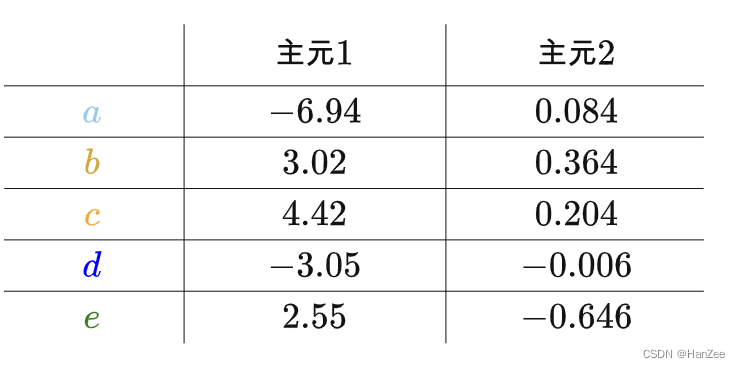
我们发现其中一个维度比重很小，忽略他的时候，对数据完整性的损失是最小的。

两个原则

那么怎么才可以找到上面所说的坐标系呢？我们遵循这两个原则：

1. 最大投影方差
2. 最小重构距离

也就是说两个随机变量之间协方差尽可能的小，单个随机变量的方差尽可能的大，这样我们降维后的数据完整性损失最小。

公式推导

定义符号：观测数据用X表示，它的协方差用C表示，旋转矩阵用P表示，旋转后的结果用Y表示，Y的协方差用D表示。

我们从上面得知，旋转后的协方差表示为：

这里P是未知的，我们就是要找到一个P：

1. 让D的对角线上的元素又大到小递减（每个随机变量的方差）。
2. 其余元素尽可能的小（也就是协方差），也就是让D尽可能的为对角矩阵。

💡那么我们现在就找到了我们的优化目标！
设我们要到的新的基：w

首先计算数据xi在基w下的投影：

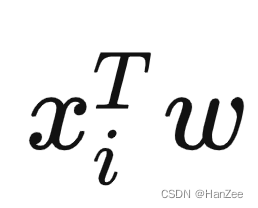
👆这里利用上面的内积的几何意义

之后，计算新的数据的方差：

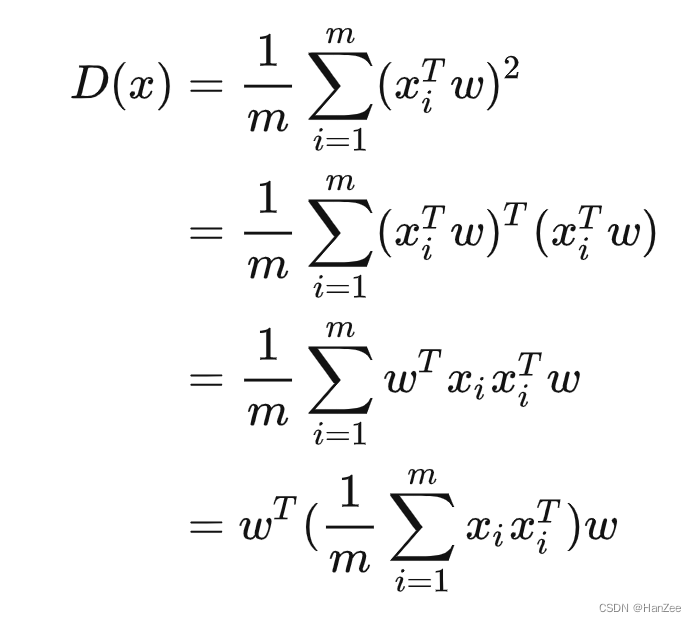
其中结果里括号的内容就是原始数据的方差（均值为0），把它用替换
设基向量的模为1，根据拉格朗日乘子法联立方程：

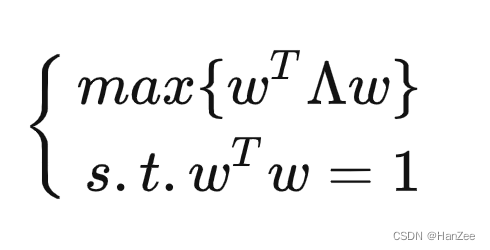
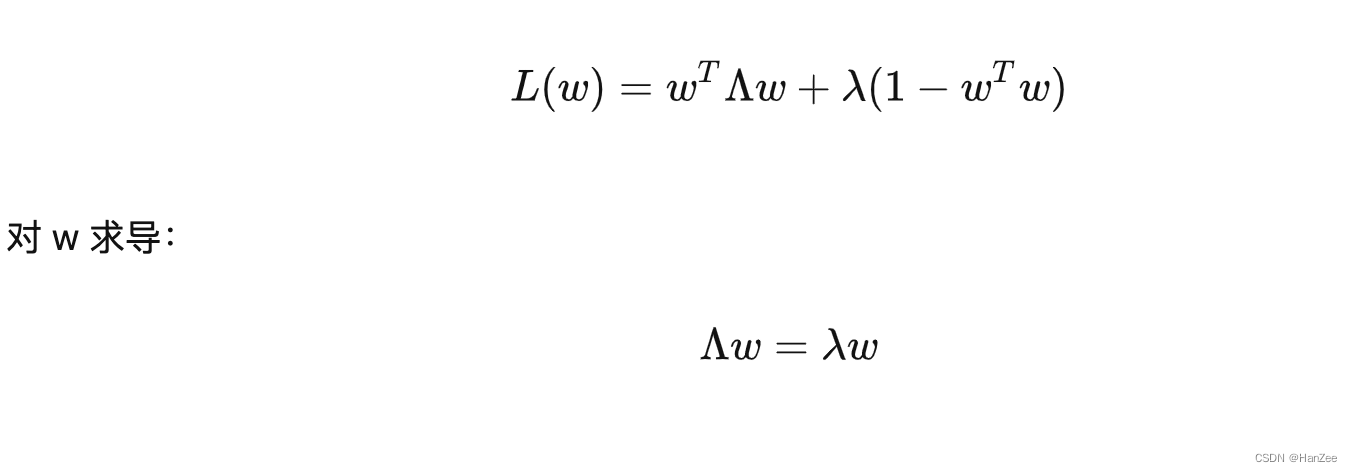
于是我们发现数据方差最大的基就是原始数据斜方差矩阵的特征值。

求解流程

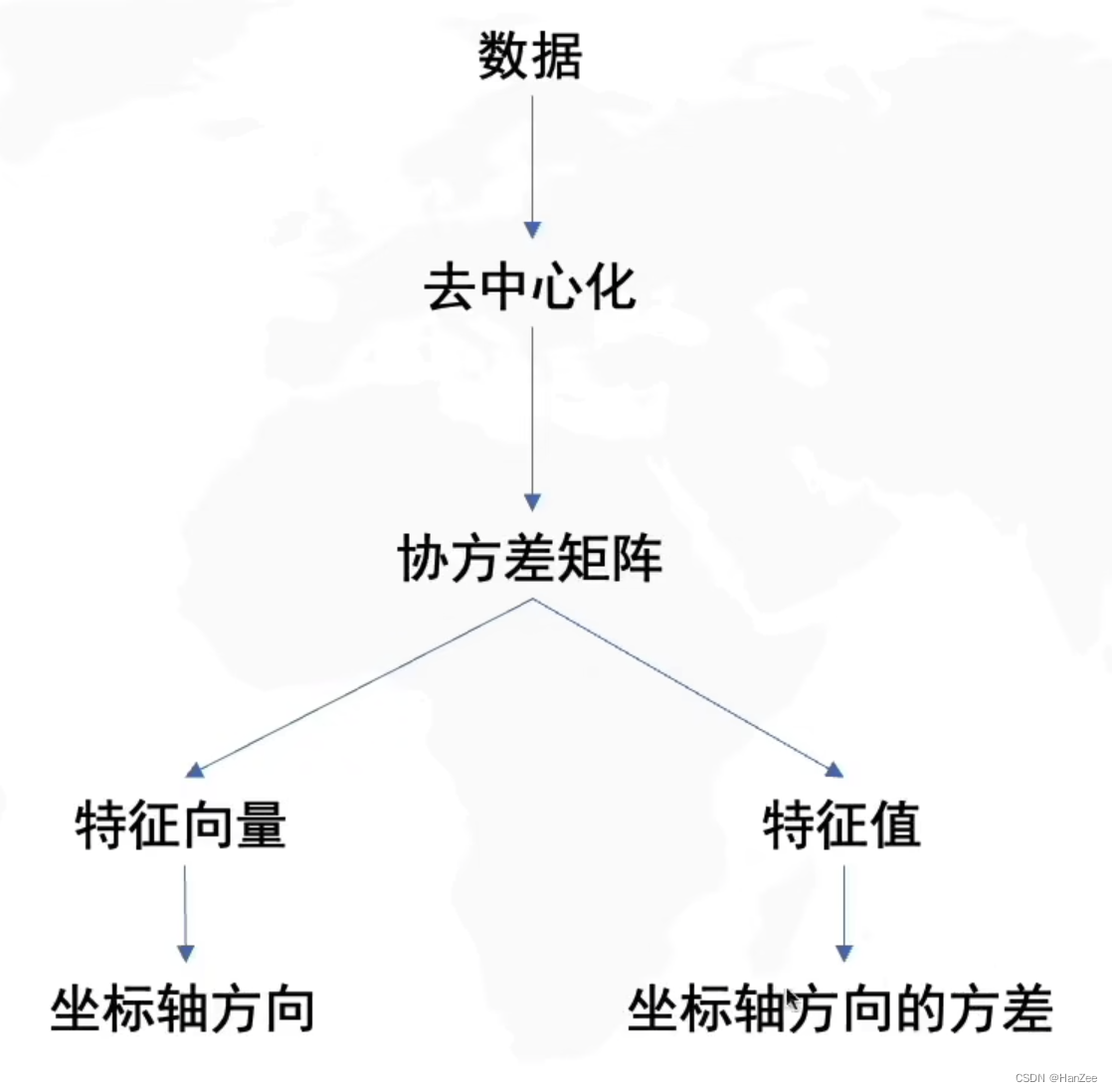
代码实现

import numpy as np
from sklearn.decomposition import PCA

# 输入待降维数据 (5 * 6) 矩阵，6个维度，5个样本值
A = np.array([[84,65,61,72,79,81],[64,77,77,76,55,70],[65,67,63,49,57,67],[74,80,69,75,63,74],[84,74,70,80,74,82]])
# 直接使用PCA进行降维
pca = PCA(n_components=2) #降到 2 维
pca.fit(A)
PCA(n_components=2)
print(pca.transform(A)) # 降维后的结果
print(pca.explained_variance_ratio_ )# 降维后的各主成分的方差值占总方差值的比例，即方差贡献率
print(pca.explained_variance_) # 降维后的各主成分的方差值

PCA的优缺点

优点

1. 仅仅需要以方差衡量信息的完整性，不受其他因素影响。
2. 各主成分之间正交，互不影响。
3. 计算简单。

缺点

1. 主成分每一个维度可解释性较弱，不如原始数据可解释性强。
2. 方差小的非主成分也可能含有对样本差异的重要信息，因此降维丢弃可能对后续数据处理有影响。
3. 降维损失数据完整性。
4. PCA 保留了主要信息，但这个主要信息只是针对训练集的，而且这个主要信息未必是重要信息。有可能舍弃了一些看似无用的信息，但是这些看似无用的信息恰好是重要信息，只是在训练集上没有很大的表现，所以 PCA 也可能加剧了过拟合；