开始学习数据结构(拖了好久终于开干了)
来自【浙江大学】数据结构(合149讲)陈越 何钦铭
Be a Fighter and Keep Fighting!!!
数据结构(data structure)定义
是计算机中存储,组织数据的方法。通常情况下,精心选择的数据结构可以带来最有效率的算法。
解决问题的效率跟 数据的组织方式, 跟空间的利用率, 算法的巧妙程度有关。
算法(algorithm)定义
- 一个有限指令集
- 接收一些输入(有些情况下不需要输入)
- 产生输出
- 一定在有限步骤之后终止
- 每一条命令必须:
- 有充分明确的目标,不可以有歧义
- 计算机能处理的范围内
- 描述应不依赖于任何一种计算机语言以及具体的实现手段
怎样选择算法
-
**空间复杂度S(n) 一 根据算法写成的程序在执行时占用存储单元的长度。**这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限,造成程序非正常中断。
-
**时间复杂度T(n) 一 根据算法写成的程序在执行时耗费时间的长度。**这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。
空间复杂度例子:
比如下面这个递归实现的函数,如果N特别大,那么每次调用的PrintN都会先把所有东西存在内存,然后等下个执行,这样会导致很容易就吃完了内存,最后直接终止掉了,而通过普通循环实现函数,无论N多大始终只有一个函数,所以没问题。

时间复杂度例子:
下面是两个多项式求和公式f(x)=a0+a1X+a2X^2+a3X^3+....a(n-1)X^(n-1)+anX^n
在运算中,加减法的速度远快于乘除法,所以下面的程序我们关注乘法,第一个程序中每次for循环都会执行(pow函数执行i-1次乘法,a[i]执行一次)i次乘法,所以总的次数为(n+1)n/2次乘法,而第二种每次for循环只执行一次乘法,所以总共n次,这样就可以知道第二种方法在N很大时候耗时更少,在时间复杂度上占优。

什么是好的算法:
分析一般算法效率时关注:
- 最坏情况复杂度Tworst(n)
- 平均复杂度Tavg(n)
- Tavg(n)<=Tworst(n)
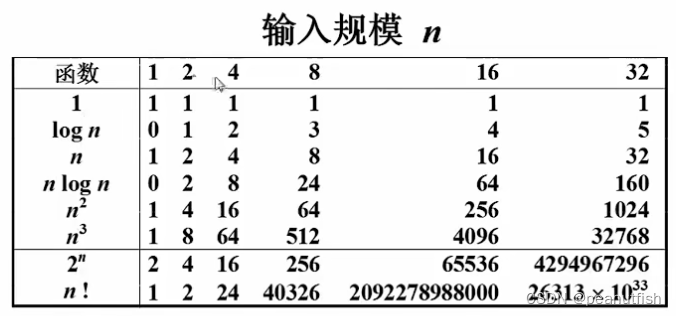
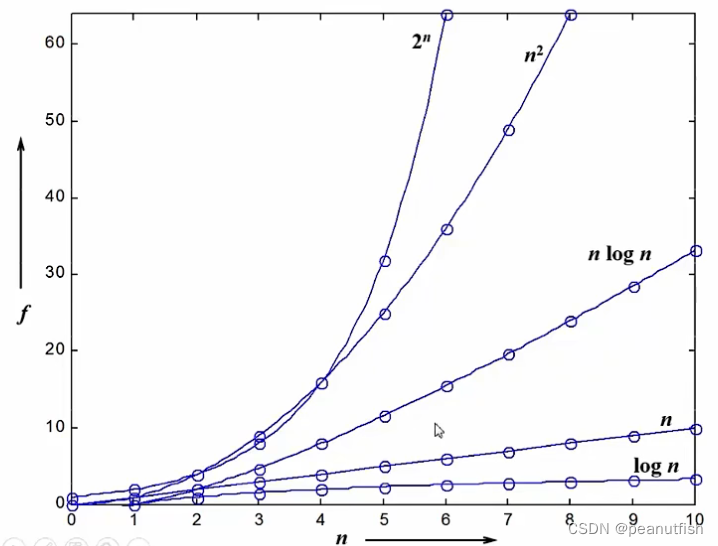
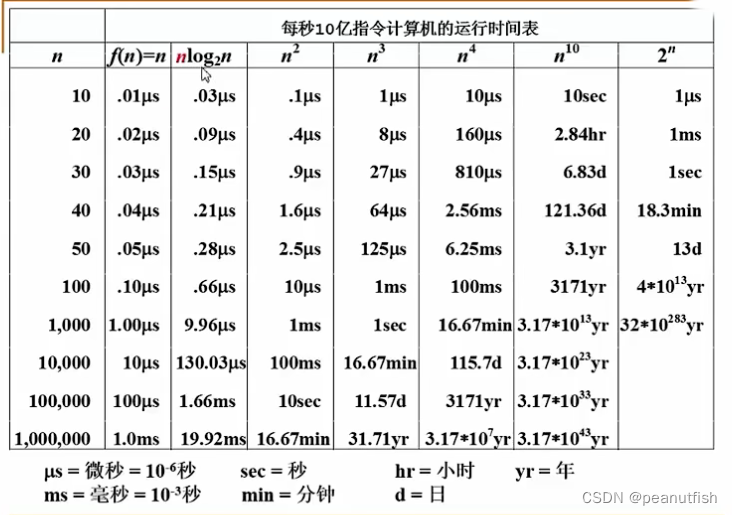
复杂度的渐进表示法: