机器学习算法之–对数几率回归(逻辑斯蒂回归)算法
上个算法(算法系列二)介绍了如何使用线性模型进行回归学习,但若要做的是分类任务,则需要找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。
虽然名字叫回归,但其实是分类学习方法
一、算法原理
对于给定的输入实例x,可求出P(Y=0|x)和P(Y=1|x)的条件概率值的大小比较,将实例x分到概率值较大的那一类。
1.1、预测函数
找出一个预测函数模型,输出值在[0,1]之间。接着,再选择一个基准值(例如0.5),若预测值》0.5,则预测为1;否则预测为0;【二分类问题】
我们可选择:
g
(
z
)
=
1
1
+
e
−
z
g(z)=\frac{1}{1+e^{-z}}
g(z)=1+e−z1作为预测函数。
该函数称为Sigmoid函数,也可称作Logistic函数(名称由来),其图形如下
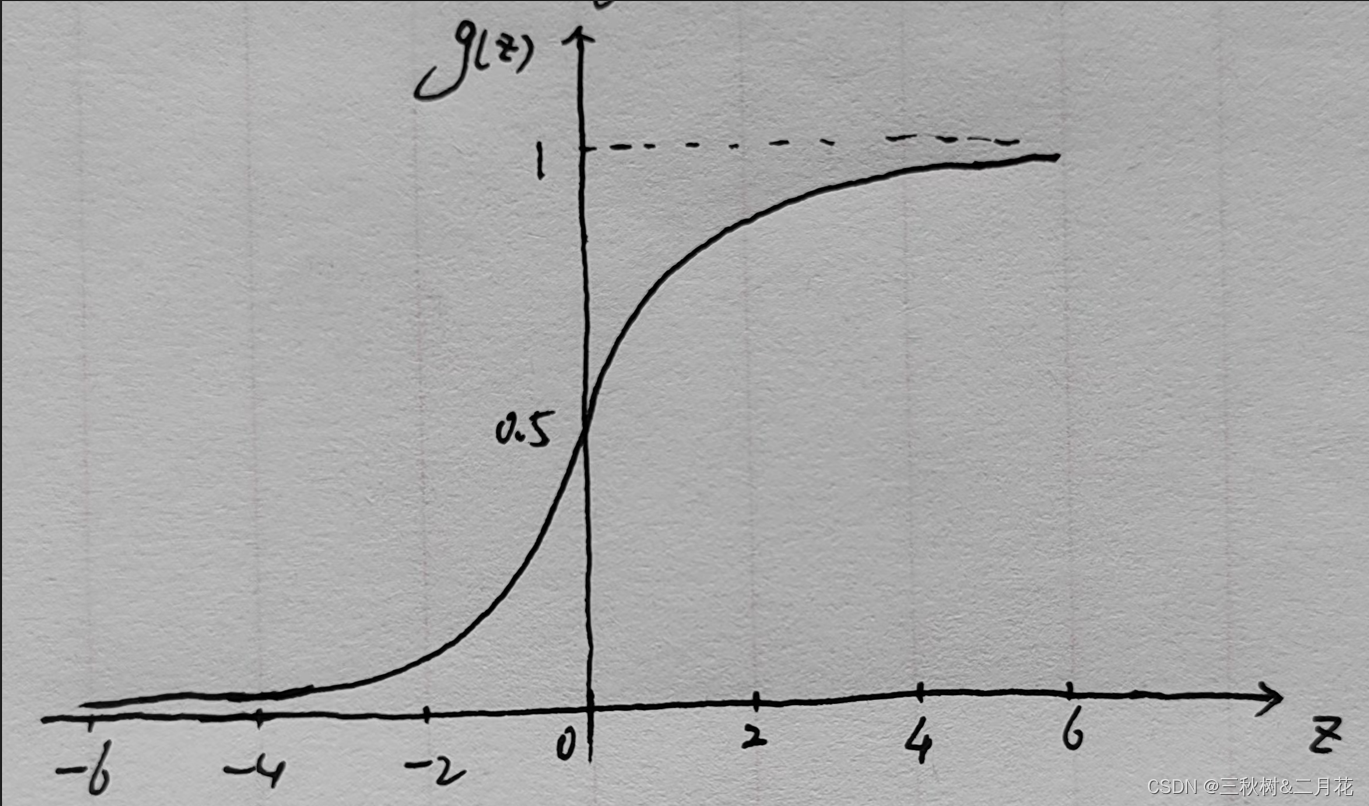
图中可以看出:
- z=0:g(z) = 0.5
- z>0:g(z) > 0.5,当z越来越大时,g(z)无限接近于1。
- z<0:g(z) < 0.5,当z越来越小时,g(z)无限接近于0。
显然,这正符合我们想要的分类方式。
我们再结合线性回归的预测函数 h θ ( x ) = θ T x h_\theta(x)=\theta^Tx hθ(x)=θTx,则逻辑斯蒂回归算法的预测函数如下: r = h θ ( x ) = g ( z ) = g ( θ T x ) = 1 1 + e − θ T x r=h_\theta(x)=g(z)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} r=hθ(x)=g(z)=g(θTx)=1+e−θTx1
此处求解的是在输入x,参数θ的前提下,y=1的概率,用概率论公式可表示为
h
θ
(
x
)
=
P
(
y
=
1
∣
x
,
θ
)
h_\theta(x)=P(y=1|x,\theta)
hθ(x)=P(y=1∣x,θ)
且必有:
P
(
y
=
1
∣
x
,
θ
)
+
P
(
y
=
0
∣
x
,
θ
)
=
1
P(y=1|x,\theta)+P(y=0|x,\theta)=1
P(y=1∣x,θ)+P(y=0∣x,θ)=1
r为正例可能性,1-r是其反例可能性,二者比值
r
1
−
r
\frac{r}{1-r}
1−rr称为“几率”,反映了x作为正例的相对可能性,进一步对几率取对数,则得到“对数几率”
l
n
r
1
−
r
ln\frac{r}{1-r}
ln1−rr
在二分类中,这是一个非黑即白的世界
实际上,这是在用线性回归模型的预测结果去逼近真是标记的对数几率,因此成为对数几率回归
对于
算法优点:
- 直接对分类可能性进行建模,无需事先假设数据分布
- 可得到近似概率预测
- 求解的目标函数是任意阶可导凸函数,数学性质very good
1.2、参数估计(如何计算θ)
在训练过程中,算法通过最大化似然函数求解θ。具体来说,似然函数表示的是P(Y|X)的条件概率。统计学家通常使用“最大似然估计”方法来进行参数估计。这种方法就是求解参数W,使得模型的似然函数在已知观测数据下最大。
l
n
P
(
y
=
1
∣
x
)
1
−
P
(
y
=
0
∣
x
)
=
θ
T
x
=
w
x
ln\frac{P(y=1|x)}{1-P(y=0|x)} = \theta^Tx=wx
ln1−P(y=0∣x)P(y=1∣x)=θTx=wx
也就是说,在逻辑回归中,输出y=1的对数几率是输入x的线性函数。
显然有,
P
(
y
=
1
∣
x
)
=
e
θ
T
x
1
+
e
θ
T
x
P
(
y
=
0
∣
x
)
=
1
1
+
e
θ
T
x
P(y=1|x)=\frac{e^{\theta^Tx}}{1+e^{\theta^Tx}}\\P(y=0|x)=\frac{1}{1+e^{\theta^Tx}}
P(y=1∣x)=1+eθTxeθTxP(y=0∣x)=1+eθTx1
设:
P
(
y
=
1
∣
x
)
=
π
(
x
)
,
P
(
y
=
0
∣
x
)
=
1
−
π
(
x
)
P(y=1|x)=\pi(x), P(y=0|x)=1-\pi(x)
P(y=1∣x)=π(x),P(y=0∣x)=1−π(x)
于是可以通过极大似然估计来估计模型参数,似然函数为
∏
i
=
1
n
[
π
(
x
i
)
]
y
i
[
1
−
π
(
x
)
]
1
−
y
i
\prod_{i=1}^n[\pi(x_i)]^{y^i}[1-\pi(x)]^{1-y^i}
i=1∏n[π(xi)]yi[1−π(x)]1−yi
对数似然函数为
L
(
w
)
=
∑
i
=
1
n
[
y
i
l
o
g
π
(
x
i
)
+
(
1
−
y
i
)
l
o
g
(
1
−
π
(
x
)
)
]
L(w)=\sum_{i=1}^n[y_ilog\pi(x_i)+(1-y_i)log(1-\pi(x))]
L(w)=i=1∑n[yilogπ(xi)+(1−yi)log(1−π(x))]
- 成本函数(所有样本的成本平均值):- 1 n L ( w ) \frac{1}{n}L(w) n1L(w)
对 L ( w ) 求极值,便可得到 w 的估计值,问题也就变成了第一对数似然函数为目标的最优化问题 L(w)求极值,便可得到w的估计值,问题也就变成了第一对数似然函数为目标的最优化问题 L(w)求极值,便可得到w的估计值,问题也就变成了第一对数似然函数为目标的最优化问题
二、模型优化
2.1、梯度下降算法、
根据梯度下降算法定义,可以得到
θ
j
=
θ
j
−
α
∂
J
(
θ
)
∂
θ
j
\theta_j=\theta_j-\alpha\frac{\partial J(\theta)}{\partial \theta_j}
θj=θj−α∂θj∂J(θ)
此处关键是求成本函数的偏导数,最终得到梯度下降算法公式
θ
j
=
θ
j
−
α
1
m
∑
i
=
1
m
(
(
h
(
x
i
)
−
y
i
)
x
j
i
)
\theta_j= \theta_j-\alpha\frac{1}{m}\sum_{i=1}^m ((h(x^i)-y^i)x_j^i)
θj=θj−αm1i=1∑m((h(xi)−yi)xji)
注意此处的形式和线性回归算法的参数迭代公式是一样的,但数值计算方法完全不同
逻辑:
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}
hθ(x)=1+e−θTx1
线性:
h
θ
(
x
)
=
θ
T
x
h_\theta(x)=\theta^Tx
hθ(x)=θTx
*除了梯度下降算法之外,还有拟牛顿法等都可以求得其最优解
三、多元分类
逻辑回归可以解决二分类问题,那如果需要分类的超过了两个类别呢?显然也是也以应对的。
假设总共有n+1个类别,y={0,1,2,3,…,n},思路是转化为二元分类
- 类别一:0,类别二:1~n,分别计算概率;
- 类别一:1,类别二:0,2~n,再分别计算概率;
- …
- 类别一:n,类别二:0~n-1,再分别计算概率。
由此可见,总共需要n+1个预测函数,分别计算P(y=0|x,θ),…,P(y=n|x,θ)
- 最后预测值: p r e d i c t i o n = m a x i ( h θ ( i ) ( x ) ) prediction=max_i(h_\theta^{(i)}(x)) prediction=maxi(hθ(i)(x))
预测出概率最高的哪个类别,就是样本所属类别
四、正则化
- 采用正则化可以用来解决模型过拟合问题
- 保留所有的特征,减少特征的权重
θ
j
\theta_j
θj的值,确保所有的特征对预测值都有少量的贡献。
当每个特征Xi对预测值Y都有少量的贡献时,这样的模型可以良好的工作,这就是正则化的目的。