有偏估计的发展及其在球谐函数拟合中的应用研究

阚昊宇
专业：大地测量与测量工程	学号：XXX
邮箱：XXX	电话：XXX

摘要：球谐函数在大地测量等领域具有重要意义，然而在观测量不多或空间分布不均匀时进行高阶球谐函数拟合，法方程系数矩阵容易严重病态，导致拟合结果不可靠。而有偏估计方法常被应用于解决由于法方程系数阵病态而导致的最小二乘估计计算不稳定问题。以中国西藏地区的GPT2w气象模型气压参数为例，对比了普通最小二乘与不同岭参数选取下的岭估计结果。结果表明，较小的岭参数能更有效的解决球谐函数拟合的不适定问题。

关键词：有偏估计；岭参数；球谐函数；GPT2w模型

Development of biased estimation and its application in spherical harmonic function fitting

Abstract: Spherical harmonic function is of great significance in geodesy and other fields. However, when high-order spherical harmonic function is fitted or when there are few observations or uneven spatial distribution, the coefficient matrix of the normal equation is prone to be seriously ill conditioned, resulting in unreliable fitting results. The biased estimation method is often used to solve the problem of unstable calculation of the least square estimation that caused by the ill conditioned coefficient matrix of the normal equation. Taking the atmospheric pressure parameters of the GPT2w meteorological model in Tibet, China as an example, the results of ordinary least squares and ridge estimation under different ridge parameters are compared. The results show that smaller ridge parameters can effectively solve the ill conditioned posed problem of spherical harmonic function fitting.

Keywords: Biased Estimation, Ridge Parameter, Spherical Harmonics; GPT2w Model

1 研究背景与意义

测量数据的参数估计是测量工作中最重要的环节之一，其对测量精度产生直接影响。最小二乘估计（Least Square Estimation，LS）是最常用的一种估计方法，在观测值误差服从正态分布的前提下，最小二乘估计为最优线性无偏估计（Best Linear Unbiased Estimate）。因此，最小二乘估计是被广泛采用的重要估计方法。但是在实际应用中，由于建立数学模型时过度参数化或是有效观测数不足，导致参数之间存在一定程度的复共线性（Multicollinearity），进而造成法方程系数矩阵病态[1]，此时需要设法减轻其对最终测量精度的影响。有偏估计的提出就是为了消除矩阵病态影响，常用的有偏估计方法有岭估计（Ridge Estimation，RE）、广义岭估计（Generalized Ridge Estimation，GRE）、主成分估计（Principal Component Estimation，PCE）等[2]。

岭估计是目前最有影响、应用最为广泛的一种有偏估计[3]，由Hoerl和Kennard于1970年提出[4]。它是根据最小二乘估计提出的一种改进的有偏估计，主要通过确定一个岭参数k来打破法方程系数阵N的复共线性，进而减弱数据呈病态性对参数估计的影响[5]。

2 国内外研究现状

3 待解决的问题及进一步研究的有关想法

线性模型发展到现在，其参数估计理论和方法研究已经具有十分丰富的理论体系，但是在一些新算法方面和特殊应用情况下还需要进一步的探讨。例如：

在评估准则方面，大部分文献考虑的是在均方误差最小化准则下进行比较，少部分文献从误差分位数进行推导，后续可以在其他准则下探讨估计的优良性，例如绝对值准则（L1正则化）、参数数量（L0正则化）等。

在参数估计方法上，有最近新提出的新型Liu估计、r-k类估计、新型主成分估计、混合估计等[14]还需进一步讨论。

最后，在约束条件方面上，大部分文献考虑的是带随机约束的线性模型，对于一些更加复杂的约束条件，例如区间约束、椭球约束、整数约束等的论述还较为缺乏，但是这些约束在实际情况中往往经常出现。例如，本文第4章将在球面上采用岭估计拟合模型。

4 算法验证：GPT2w气象模型球谐函数建模结果与分析

4.1 GPT2w经验气象模型

GPT2w是GNSS精密数据处理等领域中广泛使用的先验气象模型，由Vienna University Of Technology的Bohm等人于2014年提出[15]，列出了包括气压、温度及其垂直递减率等多项气象参数在全球范围内的1°×1°经纬分辨率的平均项、年周期项和半年周期项。

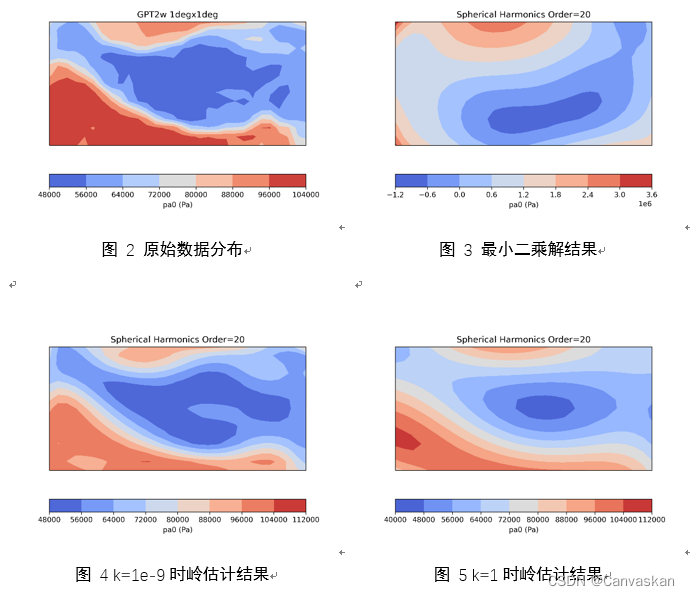
由于1°×1°的经纬分辨率，每个气象参数在全球有180×360=64800个采样，本文以中国西藏地区（经度25°~40°，纬度70°~100°）的450个采样点为例进行计算。由于气压参数的精度对于GNSS定位中天顶对流层静力学延迟（Zenith Hydrostatic Delay）的计算影响很大，因此本次实验采用其中的气压平均项参数pa0，单位为Pa，原始数据如图 2所示（为方便对比，与最小二乘估计结果、岭估计结果一起置于文末），可见西藏地区由于高原气候及山脉影响，气压变化剧烈，拟合难度较高。

4.2球谐函数

4.3最小二乘估计结果

按照普通最小二乘，其法方程系数阵N的条件数为2.7×1020，为严重病态，其最小二乘解得到的拟合参数复原结果如图 3所示，不能得到合理的模型。模型最大值超过了原始数据的三倍，最小值甚至出现了负数，这对于气压这个物理量来说是不能接受的。

4.4 岭估计结果

选取不同的岭参数k=1e-9, 1e-6, 1e-3, 1e-1和1，得到估计结果统计量为下表所示。

表 1 不同岭参数下岭估计结果统计

岭参数k	cond(N)	RMSE 单位（Pa）	残差95%分位数单位（Pa）	预计对ZHD计算影响单位（cm）
1e-9	2.0e+12	3241	5381	6
1e-6	2.0e+8	4391	7734	8
1e-3	2.0e+6	5412	9865	10
1e-1	2.0e+4	6192	10812	12
1	2.0e+3	6503	10907	12

为篇幅所限，这里仅绘出k=1e-9和1时的岭估计结果（分别为图 4和图 5），可见k=1e-9时对应的拟合样式最接近与原始数据分布，并且此时拟合的RMSE和残差95%分位数也是最小的。因此，在本次实验中，应当采用k=1e-9的岭估计。

结果表明，在球谐函数拟合时，最小二乘估计法方程病态而不能得到很好的解，但岭估计方法拟合结果较好，具有更好的可行性与有效性。

参考文献

[1] 王振杰. 大地测量中不适定问题的正则化解法研究 [D]. 中国科学院研究生院（测量与地球物理研究所）, 2003.

[2] 王其腾, 吴风华. 广义岭估计在矩阵病态问题中的应用 [J]. 华北理工大学学报(自然科学版), 2022, 44 (02): 29-34.

[3] García García C, Salmerón Gómez R, García Pérez J. A review of ridge parameter selection: minimization of the mean squared error vs. mitigation of multicollinearity [J]. Communications in Statistics - Simulation and Computation, 2022, 1-13.

[4] Hoerl A E, Kennard R W. Ridge Regression: Biased Estimation for Nonorthogonal Problems [J]. Technometrics, 1970, 12 (1): 55-67.

[5] Lukman A F, Ayinde K. Review and Classifications of the Ridge Parameter Estimation Techniques [J]. Hacettepe Journal of Mathematics and Statistics, 2016, 46 (113): 1-.

[6] Rifkin R M, Lippert R A. Notes on Regularized Least Squares [J]. 2007,

[7] J. F L, P W. A simulation study of ridge and other regression estimators [J]. Communications in Statistics - Theory and Methods, 2010, 5 (4): 307-23.

[8] Alkhamisi M, Khalaf G, Shukur G. Some Modifications for Choosing Ridge Parameters [J]. Communications in Statistics - Theory and Methods, 2006, 35 (11): 2005-20.

[9] Muniz G, Kibria B M G, Shukur G. On Developing Ridge Regression Parameters: A Graphical investigation [J]. FIU Digital Commons, 2012,

[10] Suhail M, Chand S, Kibria B M G. Quantile based estimation of biasing parameters in ridge regression model [J]. Communications in Statistics - Simulation and Computation, 2019, 49 (10): 2732-44.

[11] 黄海兰, 牛犇. 岭参数确定的研究 [J]. 测绘科学, 2011, 36 (04): 31-2.

[12] 王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法 [J]. 武汉大学学报(信息科学版), 2010, 35 (11): 1346-50.

[13] 鲁铁定. 总体最小二乘平差理论及其在测绘数据处理中的应用 [D]. 武汉大学, 2010.

[14] 周星晔. 测量误差模型下的三种新的有偏估计方法 [D]. 重庆大学, 2021.

[15] Böhm J, Möller G, Schindelegger M, 等. Development of an improved empirical model for slant delays in the troposphere (GPT2w) [J]. GPS Solutions, 2014, 19 (3): 433-41.

[16] Ambs P, Sanchez-Mondragon J, Beyette J F R, 等. Data fitting on a spherical shell [A], Wave Optics and Photonic Devices for Optical Information Processing II [C]. 2003.

[17] 覃宇欣, 黄海兰. 吉洪诺夫正则化总体最小二乘的圆曲线拟合 [J]. 测绘科学, 2021, 46 (05): 33-7+65.