我的首个python的合集啊~~  完全给自己看啊 不喜喷了也不里你

一、一维插值

对现有数据进行拟合或插值是数学分析中常见的方式。

• 通过分析现有数据，得到一个连续的函数（也就是曲线）；或者更密集的离散方程与已知数据互相吻合，这个过程叫做拟合。

• 通过已知的、离散的数据点，在范围内推求新数据点的过程或方法则叫做插值

简单来说，插值与拟合最大的区别就是，插值所获得的曲线一定要通过数据点，而拟合需要的是总体上最接近的结果。

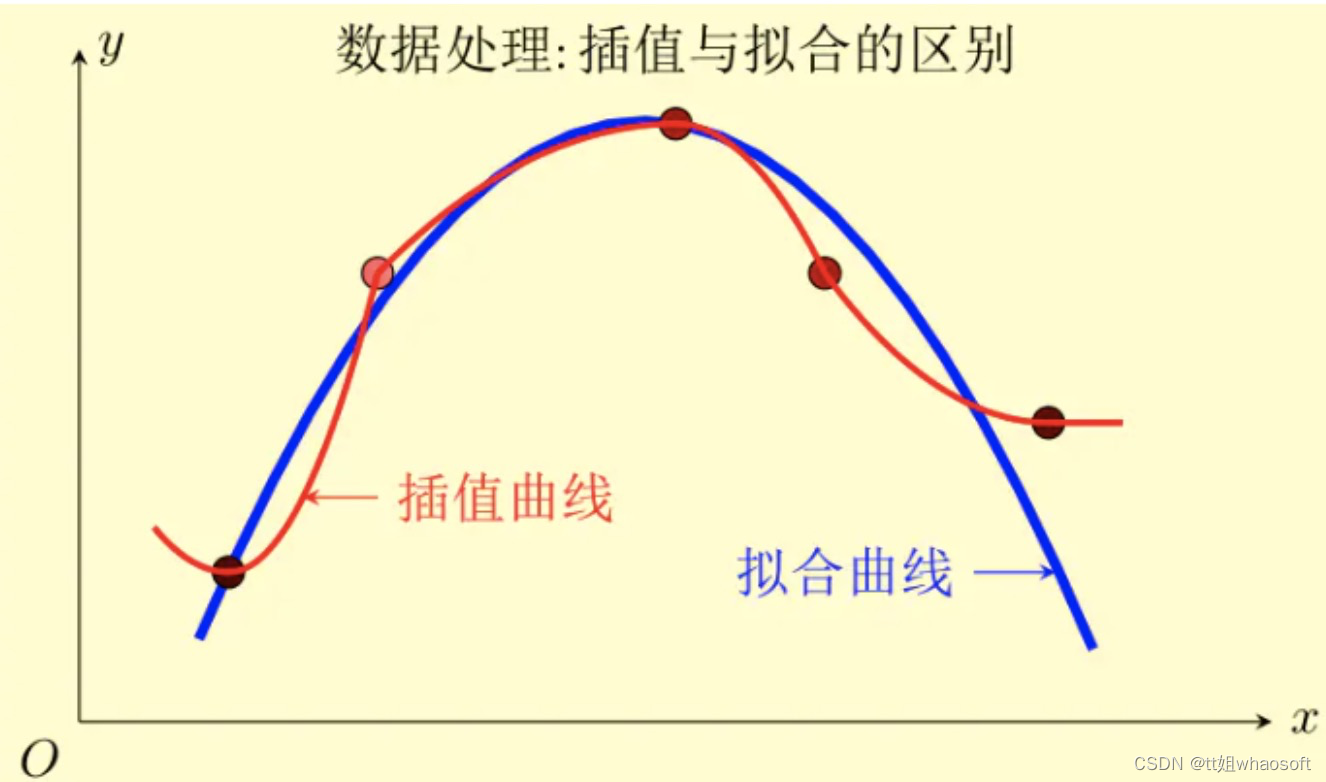
所以说要实现插值算法，我们的目标是通过给定的x值和y值，创建一个函数y=f(x)，可以在该函数中插入想要的任何值a并获得相应的值y=f(a)。

例如给定x=[0:5:5]，y=x^2，在python中画出散点图为

import numpy as npimport matplotlib.pyplot as pltx_data = np.linspace(0,5,5)y_data = x_data**2plt.scatter(x_data,y_data)plt.show()

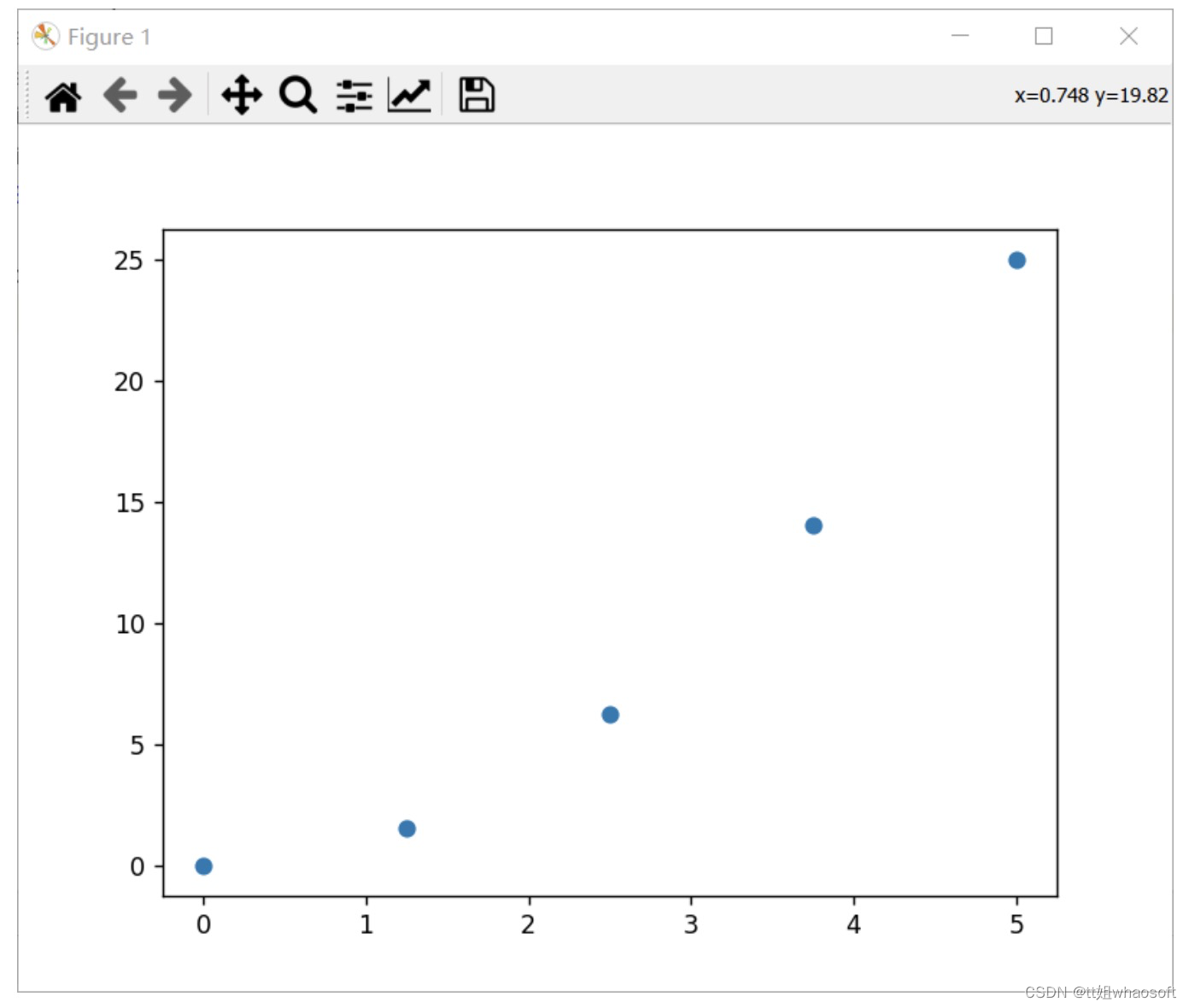 假如我们想获取x=2的值，可以看到图中没有对应的数据点，因此无法直接获得，所以需要用到插值，而最简单的插值方式为线性插值，就是通过直线连接数据点。

这样通过scipy.interpolate.interp1d()的函数即可进行一维插值。

from scipy.interpolate import interp1dx_data = np.linspace(0,5,5)y_data = x_data**2y_f = interp1d(x_data, y_data, 'linear')print(y_f(2))

通过上述代码使用线性插值，运行代码后求出x=2时y的值为4.375，由于线性插值是通过相邻两点的连线来进行插值，无法考虑到其他数据点，我们都知道x=2时y=x^2的值为4，这里的插值结果明显有问题。

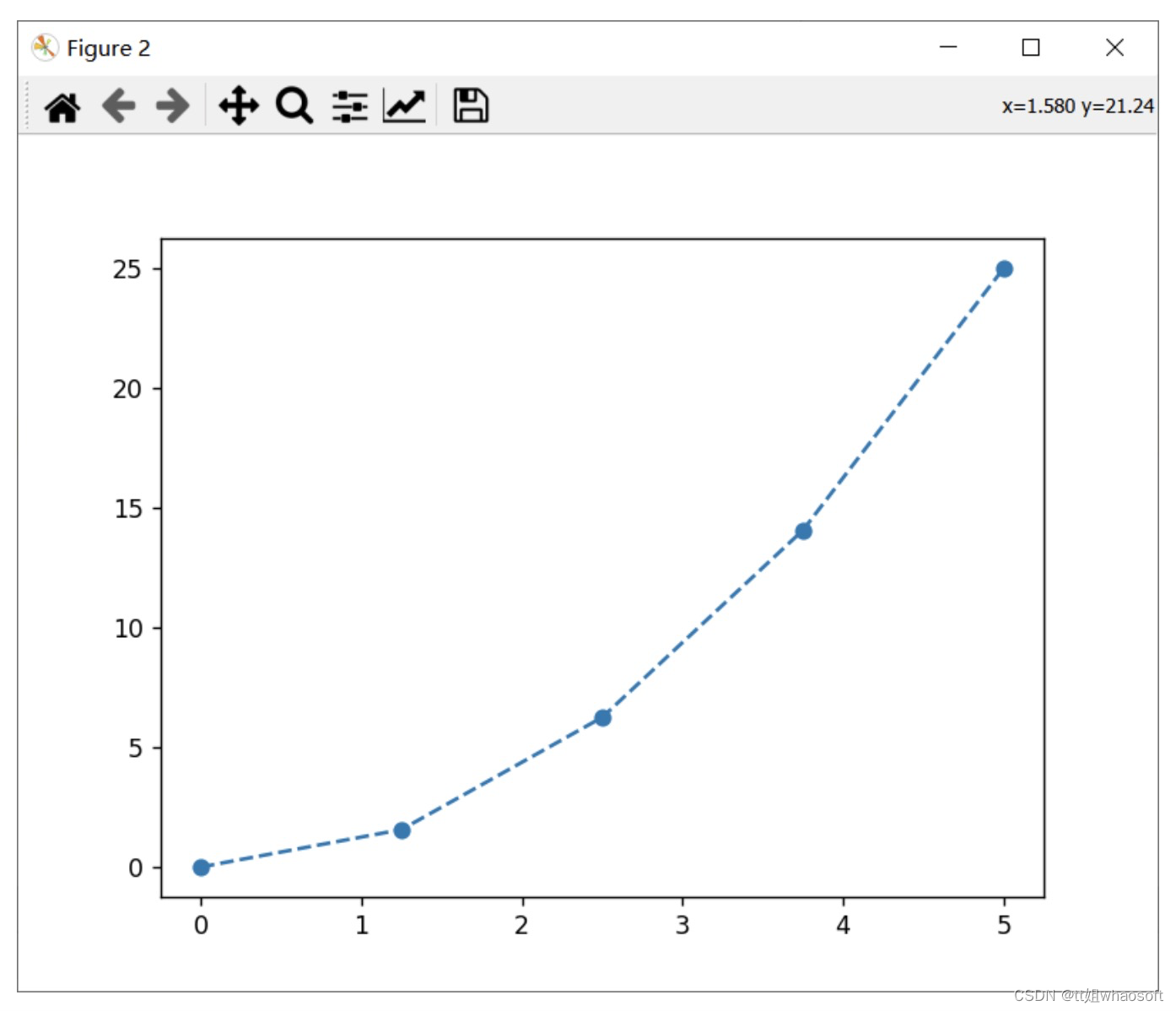
于是使用2次多项式的方式进行插值，可以得到y(2)=4​​​​​​​

y_f = interp1d(x_data, y_data,'quadratic')x = np.linspace(0,5,100)y = y_f(x)plt.plot(x,y,'--')plt.show()print(y_f(2))

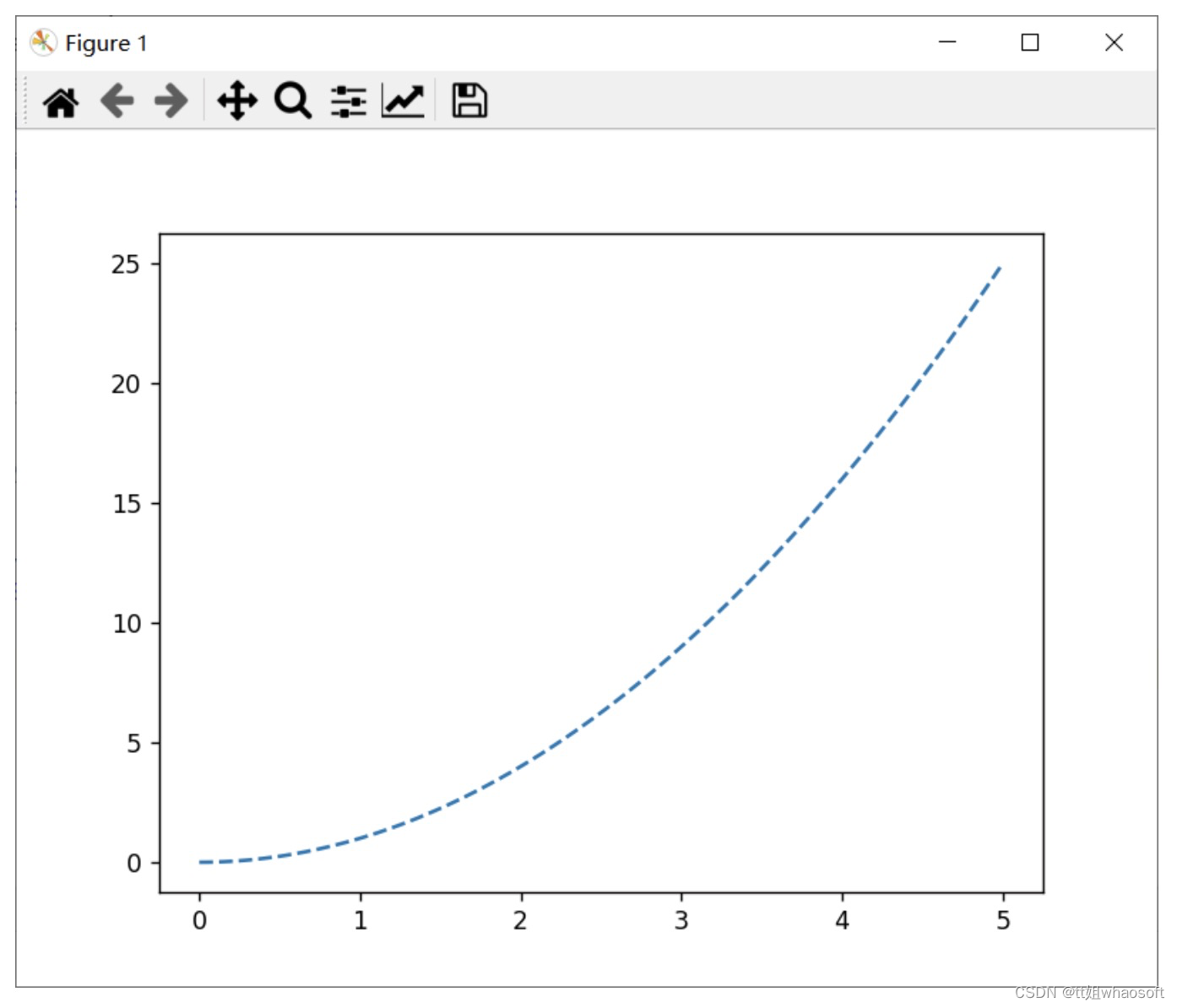
上述案例的数据较为简单，我们可以轻易地判断插值后的数据是否准确，但是对于复杂的数据，选择合适的插值方式就变得十分重要。 

 

二、二维插值

一维插值就是一维插值就是给出y=f(x)上的点(x1,y1),(x2,y2),…,(xn,yn)，由此求出y=f(x)在点xa处的值ya的值。

在此基础上进行扩展，二维插值就是给出z=f(x,y)上的点(x1,y1,z1),…,(xn,yn,zn)，由此求出在(xa,ya)处求出za的值。

使用Scipy中的interpolate.interp2d函数可以实现二维插值。

class scipy.interpolate.interp2d(x, y, z, kind='linear', copy=True, bounds_error=False, fill_value=None)

定义数据点坐标的数组。如果这些点位于规则网格上，x 可以指定列坐标，y 可以指定行坐标，例如：

x = [0,1,2];  y = [0,3]; z = [[1,2,3], [4,5,6]]

否则，x 和 y 必须指定每个点的完整坐标，例如：

x = [0,1,2,0,1,2];  y = [0,0,0,3,3,3]; z = [1,4,2,5,3,6]

如果 x 和 y 是多维的数组，则会在使用前将它们展平。

我们使用以下代码绘图进行示例：​​​​​​​

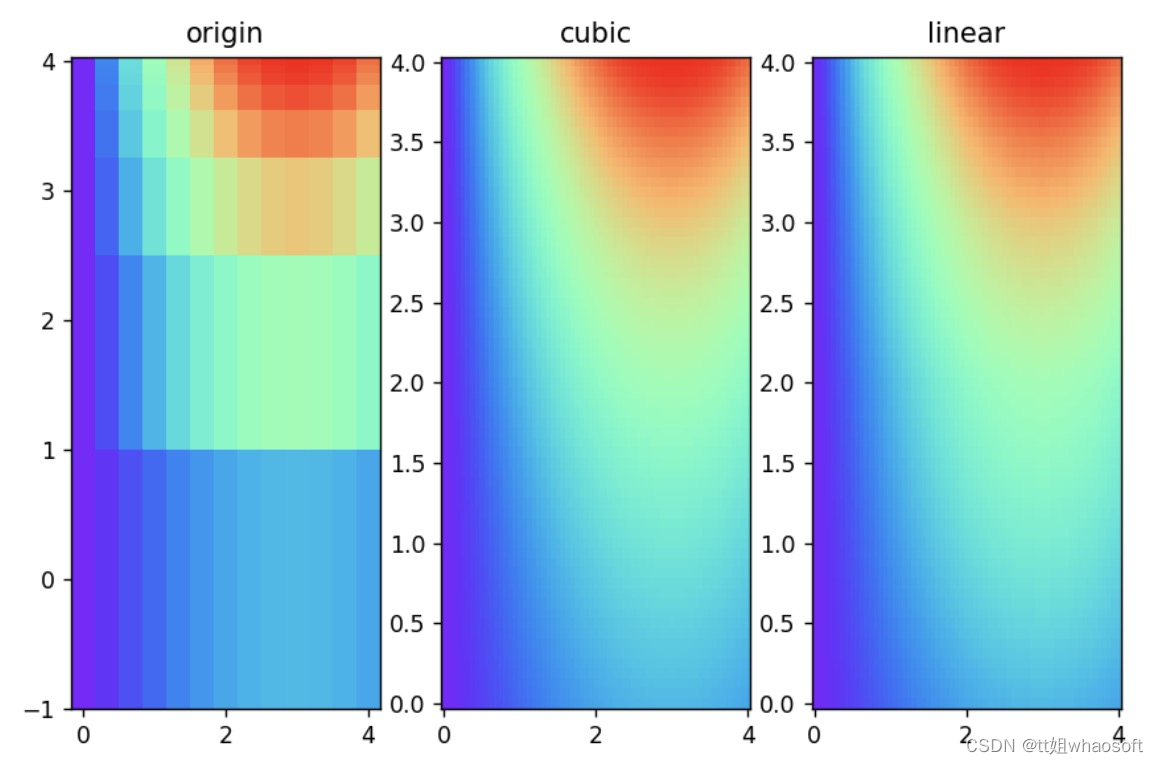
import numpy as npfrom scipy.interpolate import interp2dimport matplotlib.pyplot as pltx = np.linspace(0, 4, 13)y = np.array([0, 2, 3, 3.5, 3.75, 3.875, 3.9375, 4])X, Y = np.meshgrid(x, y)Z = np.sin(np.pi*X/6) * np.exp(Y/3)x2 = np.linspace(0, 4, 65)y2 = np.linspace(0, 4, 65)f1 = interp2d(x, y, Z, kind='cubic')Z2 = f1(x2, y2)f2 = interp2d(x,y,Z,kind='linear')Z3 = f2(x2,y2)fig, ax = plt.subplots(nrows=1, ncols=3)ax[0].pcolormesh(X, Y, Z,cmap='rainbow')X2, Y2 = np.meshgrid(x2, y2)ax[1].pcolormesh(X2, Y2, Z2,cmap='rainbow')X3, Y3 = np.meshgrid(x2, y2)ax[2].pcolormesh(X3, Y3, Z3,cmap='rainbow')ax[0].set_title('origin')ax[1].set_title('cubic')ax[2].set_title('linear')plt.show()

可以通过图片对比各插值方式的区别。

 

三、几种一维插值方式对比

使用python的scipy库可进行一维插值，并且对比了线性（linear）和二次多项式（quadratic）两种方法，这里主要来介绍一下scipy.interpolate.interp1d函数的其他插值选项。

首先，interp1d函数由以下部分所组成

class scipy.interpolate.interp1d(x, y, kind='linear', axis=- 1, copy=True, bounds_error=None,fill_value=nan, assume_sorted=False)

• x为一维数组

• y可以是N维数组，但y 沿插值轴的长度必须等于 x 的长度

• kind表示插值的方式（默认为‘linear’），包括 ‘linear’, ‘nearest’, ‘nearest-up’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’, ‘previous’, or ‘next’.

  “zero”、“linear”、“quadratic”和“cubic”是指零、一、二或三阶的样条插值；

  ‘previous’ 和 ‘next’ 只是返回该点的上一个或下一个值

  'nearest-up' 和 'nearest' 在对半整数（例如 0.5、1.5）进行插值时有所不同，“nearest-up”向上取整，“nearest”向下取整。

• axis用于指定沿其进行插值的 y 轴。默认为最后一个y轴。

• copy（布尔类型）如果为 True，则该类函数创建 x 和 y 的内部副本。如果为 False，则使用对 x 和 y 的引用。默认是True。

• bounds_error（布尔类型）如果为 True，则在任何时候尝试对 x 范围之外的值进行插值时都会引发 ValueError（需要外插）。如果为 False，则为越界值分配 fill_value。默认情况下会报错，除非fill_value="extrapolate"。

• fill_value，如果是 ndarray（或浮点数），则此值将用于填充数据范围之外的请求点。如果未提供，则默认值为 NaN。类数组必须正确广播到非插值轴的尺寸。如果是双元素元组，则第一个元素用作 x_new < x[0] 的填充值，第二个元素用于 x_new > x[-1]。任何不是 2 元素元组的东西（例如，列表或 ndarray，无论形状如何）都被视为一个类似数组的参数，用于两个边界，如下所示，上面 = fill_value，fill_value。使用二元素元组或 ndarray 需要 bounds_error=False。

我们使用下述代码绘图进行对比

​​​​​​​

import numpy as npfrom scipy.interpolate import interp1dimport pylabA, nu, k = 10, 4, 2def f(x, A, nu, k):    return A * np.exp(-k*x) * np.cos(2*np.pi * nu * x)xmax, nx = 0.5, 8x = np.linspace(0, xmax, nx)y = f(x, A, nu, k)f_nearest = interp1d(x, y,'nearest')f_linear  = interp1d(x, y,'linear')f_cubic   = interp1d(x, y,'cubic')f_next    = interp1d(x, y, 'next')x2 = np.linspace(0, xmax, 100)pylab.plot(x, y, 'o', label='data points')pylab.plot(x2, f(x2, A, nu, k), label='exact')pylab.plot(x2, f_nearest(x2), label='nearest')pylab.plot(x2, f_linear(x2), label='linear')pylab.plot(x2, f_cubic(x2), label='cubic')pylab.plot(x2, f_next(x2), label='next')pylab.legend(loc=1)pylab.show()

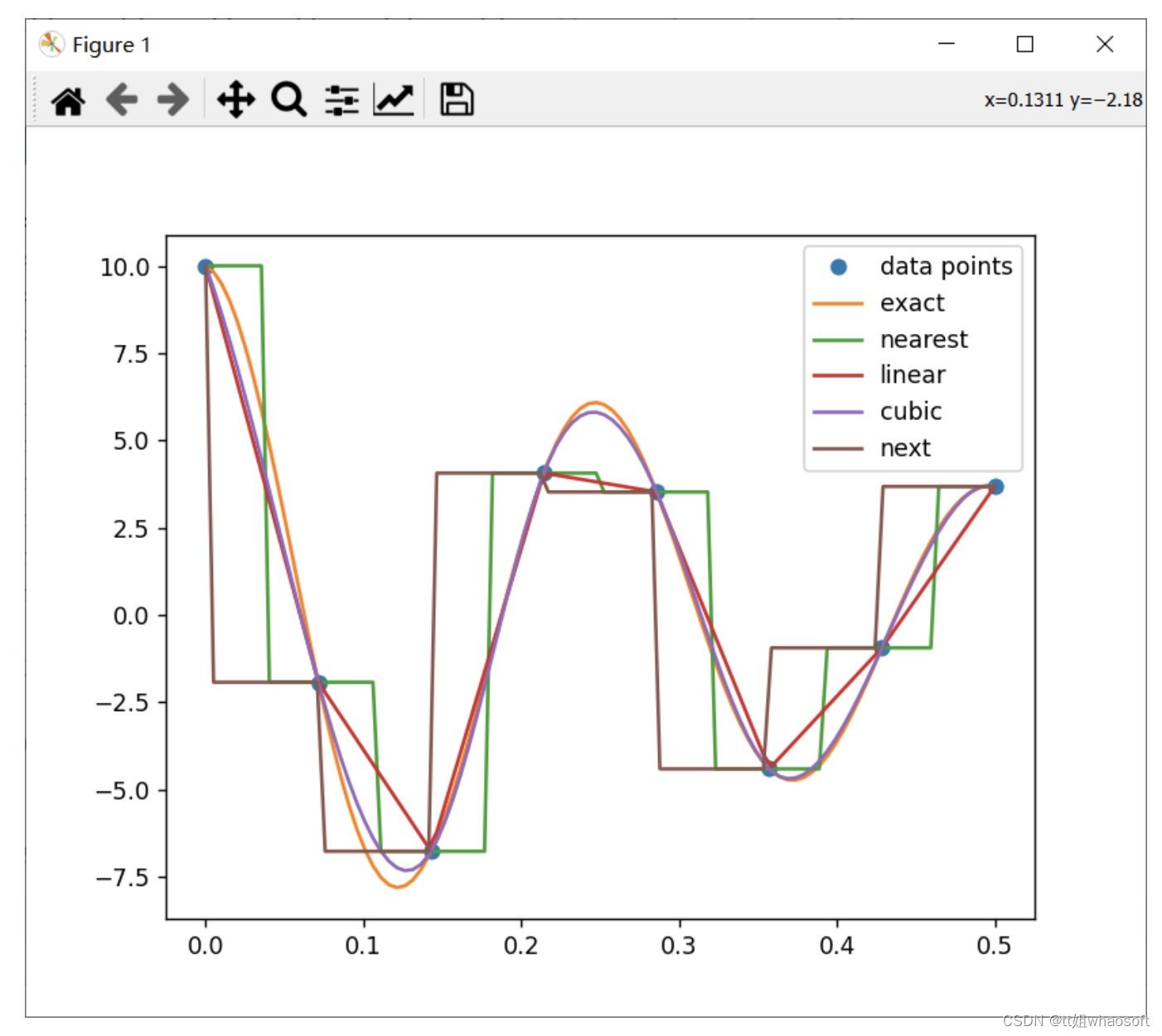
可以通过上图对比各插值方式与原函数（exact）的曲线区别。

 

四、曲线拟合

在处理数据时经常需要进行曲线拟合，在拟合过程中我们采用了插值的思想。

对于给定的数据x=[...]和y=[...]，插值的目的是找到参数β的最优集合，使函数

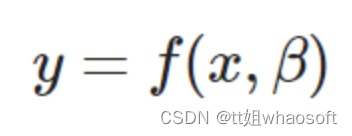
能够与原数据最为相似。

• 其中一种方法是通过调整β使：

•  

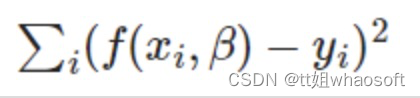
• 能够最小化，这种方法称之为最小二乘法。

• 如果yi的值有相应的误差，那么使下式最小化

•  

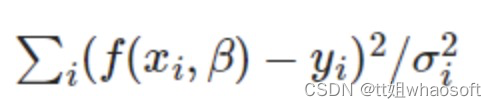
• 称之为β的最大似然估计。在给定xi与yi的情况下，这样得到的β值最为准确。

我们给定以下随机数据点并绘制散点图：​​​​​​​

import numpy as npimport matplotlib.pyplot as pltimport pandas as pdfrom scipy.optimize import curve_fitx_data = np.array([0.        , 0.15789474, 0.31578947, 0.47368421, 0.63157895,       0.78947368, 0.94736842, 1.10526316, 1.26315789, 1.42105263,       1.57894737, 1.73684211, 1.89473684, 2.05263158, 2.21052632,       2.36842105, 2.52631579, 2.68421053, 2.84210526, 3.        ])y_data = np.array([  2.95258285,   3.49719803,  -2.1984975 ,  -4.88744346,        -7.41326345,  -8.44574157, -10.01878504, -13.83743553,       -12.91548145, -16.41149046, -14.93516299, -13.42514157,       -14.12110495, -17.6412464 , -16.1275509 , -17.11533771,       -15.66076021, -12.48938865, -11.33918701, -11.70467566])plt.scatter(x_data,y_data)plt.show()

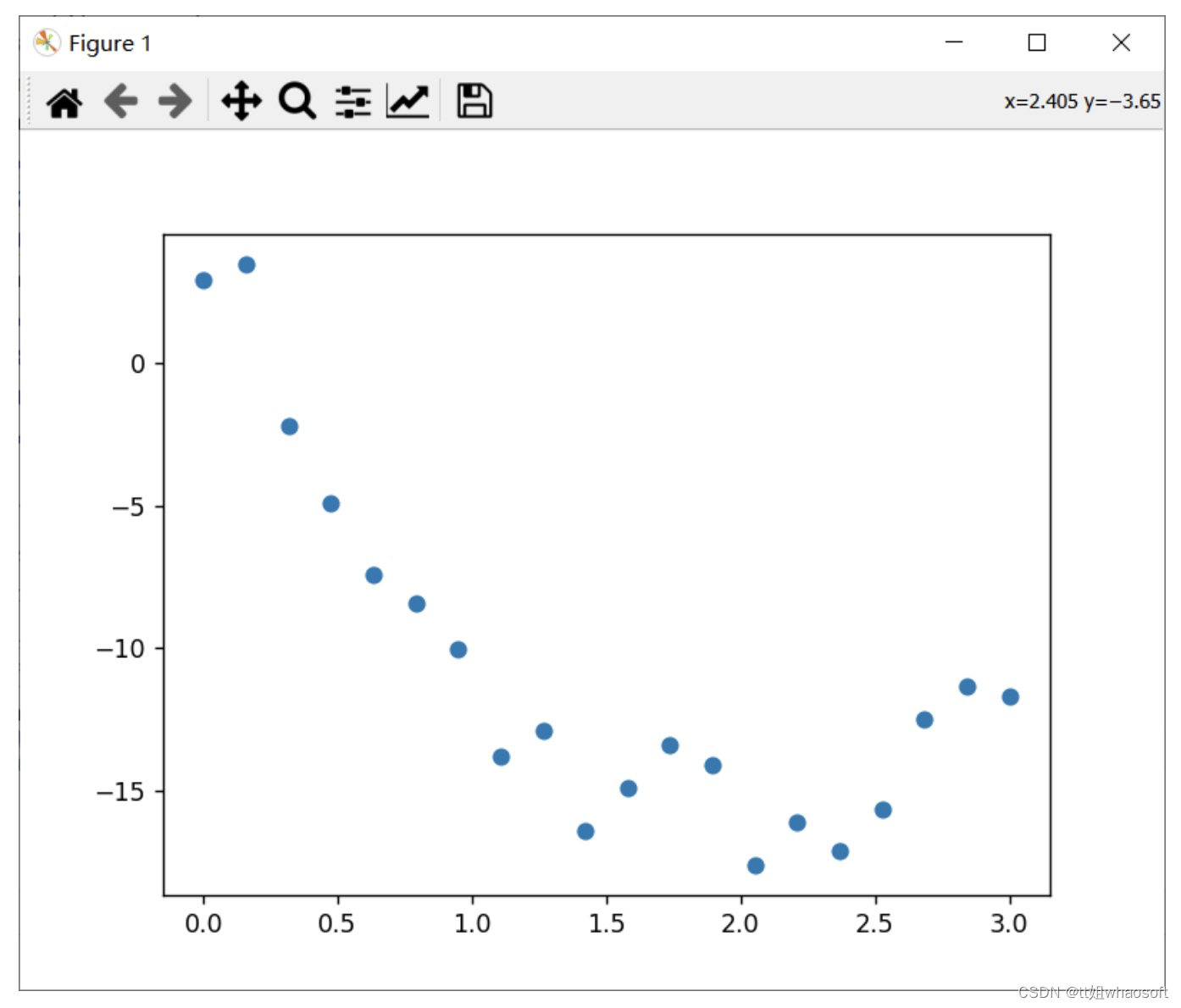
 我们使用下式的模型进行拟合：

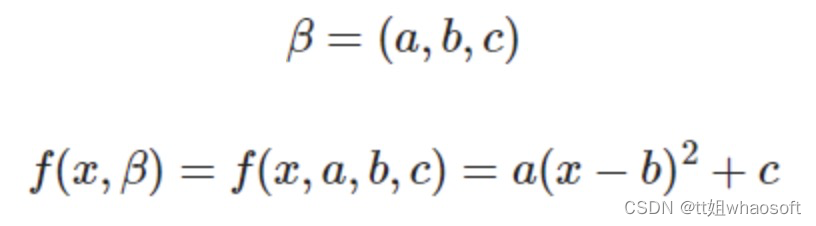
我们需要求解出符合上述数据点的最优的a、b、c的值，需要在python中：

（1）需要定义模型方程；

（2）使用scipy库中的curve_fit函数，使用该函数时需要定义一个β的初始值，对于一些复杂的模型，初始值决定了函数能否顺利运算。

下面定义函数并进行拟合​​​​​​​

def fitfun(x, a, b, c):    return a*(x-b)**2 + cpopt, pcov = curve_fit(fitfun, x_data, y_data, p0=[3,2,-16])

其中：

popt为我们定义的函数fitfun的最佳参数。

pcov为协方差矩阵，用于给定误差。

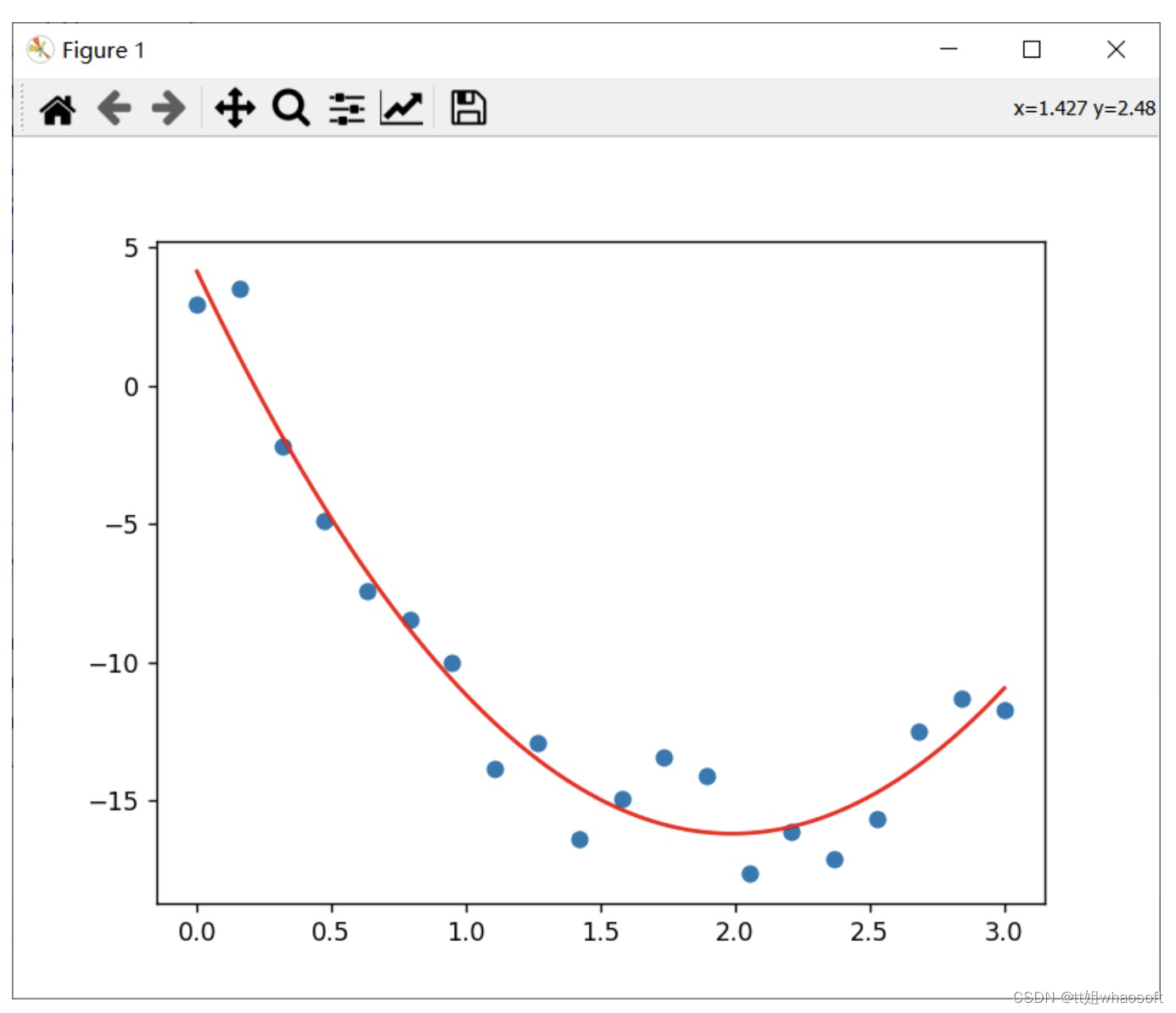
接下来我们就可以绘制出拟合好的曲线​​​​​​​

a, b, c = poptx_model = np.linspace(min(x_data), max(x_data), 100)y_model = fitfun(x_model, a, b, c)plt.scatter(x_data,y_data)plt.plot(x_model,y_model, color='r')plt.show()

 whaosoft aiot http://143ai.com