图像渐变

为了比原始像素值做得更好，我们必须以某种方式将像素“组织”成更多信息的单元。相邻像素之间的差异通常非常有用。像素值通常在对象边界、存在阴影、图案内或纹理表面上不同。相邻像素之间的值差异称为图像梯度。

计算图像梯度最简单的方法是分别计算图像的水平 (x) 和垂直 (y) 轴上的差异，然后将它们组合成一个 2D 向量。这涉及两个 1D 差分运算，可以方便地用矢量掩码或滤波器表示。掩码 [1, 0, –1] 根据我们应用掩码的方向，获取左邻居和右邻居或上邻居和下邻居之间的差异。也有 2D 梯度过滤器，但为了本示例的目的，1D 过滤器就足够了。

申请一个过滤图像，我们执行卷积。它涉及翻转过滤器并使用一小块图像进行内积，然后移动到下一个补丁。卷积在信号处理中很常见。我们将使用 * 来表示操作：

[ abc ] * [1 2 3] = c *1 + b *2 + a *3

像素 ( i , j ) 处的x和y梯度为：

 它们一起形成梯度：

 矢量可以完全用它的方向和大小来描述。梯度的大小等于梯度的欧式范数gx2+gy2，它表示像素值围绕像素变化的程度。渐变的方向或方向取决于水平和垂直方向变化的相对大小；它可以计算为θ=arctan(gy/gx). 图 8-2说明了这些数学概念。

图 8-3说明了由垂直和水平梯度组成的简单图像梯度的示例。每个示例都是九个像素的图像。每个像素都标有灰度值。（较小的数字对应较深的颜色。）中心像素的渐变显示在每个图像下方。左边的图像包含水平条纹，颜色仅在垂直方向上变化。因此，水平方向梯度为零，垂直方向梯度不为零。中心图像包含垂直条纹；因此，水平梯度为零。右边的图像包含对角线条纹，渐变也是对角线的。

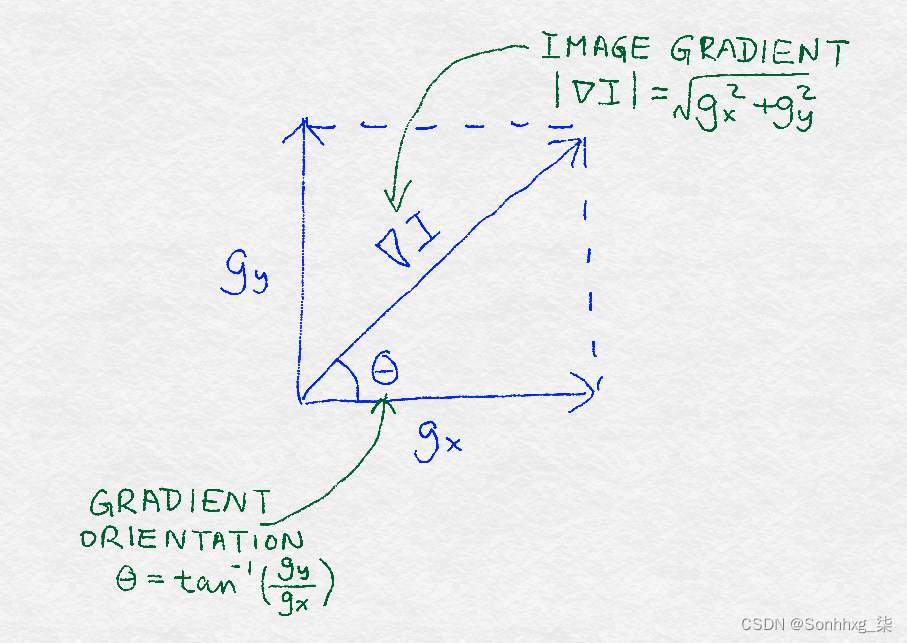
图 8-2。图像梯度定义的图示

 

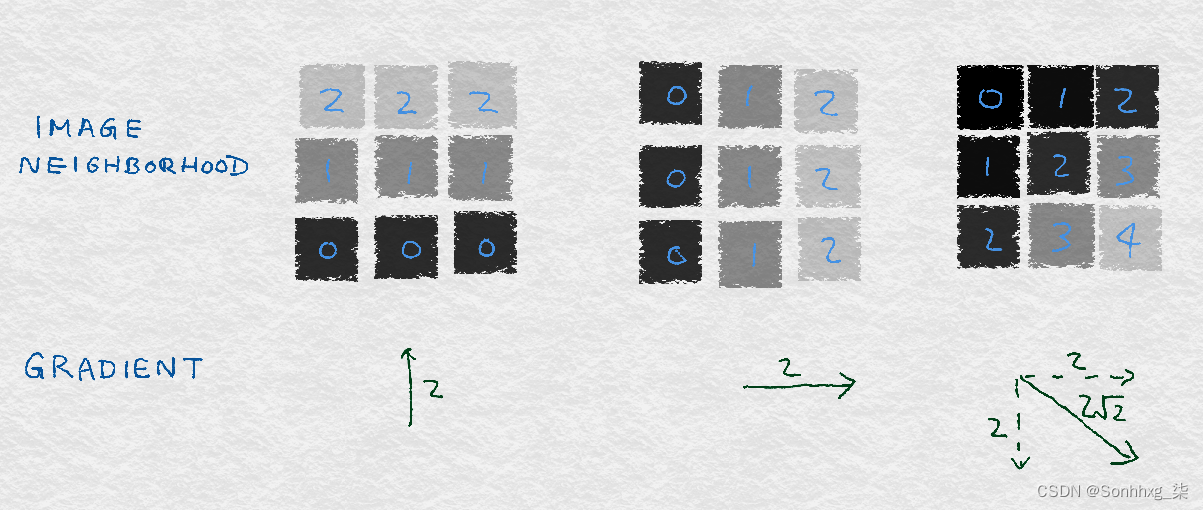
图 8-3。图像渐变的简单例子

该定义适用于合成玩具示例。但它在真实图像上效果好吗？在示例 8-1中，我们使用一张来自 的猫图片对其进行检查，如图 8-4scikit-image所示，其水平和垂直渐变。由于梯度是在每个像素位置计算的原始图像，我们最终得到两个新矩阵，每个矩阵都可以可视化为图像。

import matplotlib.pyplot as plt
import numpy as np
from skimage import data, color

### Load the example image and turn it into grayscale
image = color.rgb2gray(data.chelsea())

### Compute the horizontal gradient using the centered 1D filter.
### This is equivalent to replacing each non-border pixel with the
### difference between its right and left neighbors. The leftmost
### and rightmost edges have a gradient of 0.
gx = np.empty(image.shape, dtype=np.double)
gx[:, 0] = 0
gx[:, -1] = 0
gx[:, 1:-1] = image[:, :-2] - image[:, 2:]

### Same deal for the vertical gradient
gy = np.empty(image.shape, dtype=np.double)
gy[0, :] = 0
gy[-1, :] = 0
gy[1:-1, :] = image[:-2, :] - image[2:, :]

### Matplotlib incantations
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, 
                                    figsize=(5, 9), 
                                    sharex=True, 
                                    sharey=True)

ax1.axis('off')
ax1.imshow(image, cmap=plt.cm.gray)
ax1.set_title('Original image')
ax1.set_adjustable('box-forced')

ax2.axis('off')
ax2.imshow(gx, cmap=plt.cm.gray)
ax2.set_title('Horizontal gradients')
ax2.set_adjustable('box-forced')

ax3.axis('off')
ax3.imshow(gy, cmap=plt.cm.gray)
ax3.set_title('Vertical gradients')
ax3.set_adjustable('box-forced')

请注意，水平梯度会挑选出强烈的垂直图案，例如猫眼的内边缘，而垂直梯度会挑选出强烈的水平图案，例如胡须和眼睛的上下眼睑。乍一看，这似乎有点自相矛盾，但一旦我们仔细考虑一下，它就会变得有道理。水平 ( x ) 梯度标识水平方向的变化。强烈的垂直图案在大致相同的x位置跨越多个y像素。因此，垂直图案会导致像素值的水平差异。这也是我们的眼睛检测到的。 

梯度方向直方图

单个图像梯度可以挑出图像邻域中的微小差异。但我们的眼睛看到的模式比这更大。例如，我们看到了整根猫的胡须，而不仅仅是一小部分。人类视觉系统识别区域中的连续模式，因此我们仍然需要做更多的工作来总结邻域中的图像梯度。

我们究竟如何总结向量？统计学家会回答：“看看分布！” SIFT 和 HOG 都走这条路。特别是，他们将梯度向量的（归一化）直方图计算为图像特征。直方图将数据划分为 bin 并计算每个 bin 中有多少个数据点；这是一个（非标准化的）经验分布。归一化确保计数总和为 1。数学语言是它具有单位ℓ1规范。

图像梯度是一个向量，向量可以由两个分量表示：方向和大小。因此，我们仍然需要决定如何设计直方图以将这两个组件都考虑在内。SIFT 和 HOG 确定了一种方案，其中图像梯度由它们的方向角θ 装箱，由每个梯度的大小加权。这是程序：

1. 将 0°–360° 划分为大小相等的 bin。

2. 对于邻域中的每个像素，将权重w添加到对应于其方向θ的 bin 。w是梯度大小和其他相关信息的函数。例如，该信息可能是像素到图像块中心的倒数距离。这个想法是，如果梯度很大，权重应该很大，并且图像邻域中心附近的像素比距离较远的像素更重要。

3. 标准化直方图。

图 8-5提供了由 4×4 像素的图像邻域组成的 8 个 bin 的梯度方向直方图的图示。

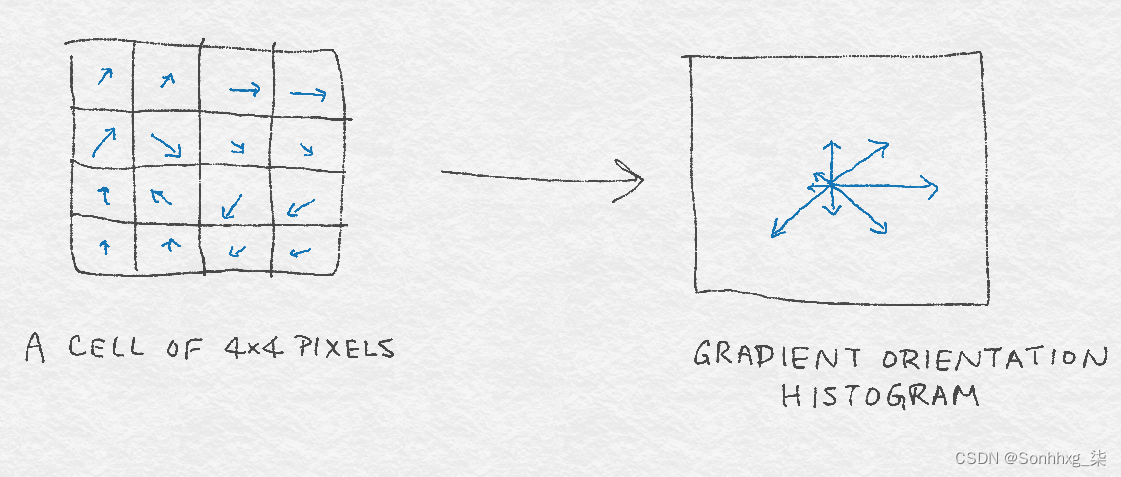
图 8-5。基于 4 × 4 方形像素单元的梯度的 8 个 bin 的梯度方向直方图图示

当然，在基本的梯度方向直方图算法中有许多旋钮可以调整，还有一些可选的附加功能。与往常一样，正确的设置可能在很大程度上取决于要分析的特定图像。

接下来让我们检查一些要做出的决定以及这些决定可能对您的模型产生的影响。

应该使用什么权重函数？

HOG论文比较各种梯度大小加权方案：幅度本身，它的平方或平方根，二值化，或在高端或低端剪裁。没有修饰的普通星等在作者的实验中表现最好。

SIFT 还使用梯度的普通大小。此外，它希望避免图像窗口位置的微小变化导致特征描述符突然变化，因此它使用从窗口中心测量的高斯距离函数来降低来自邻域边缘的梯度。换句话说，梯度幅度乘以12πσ2e-∥p-p0∥2/2σ2，其中p是生成梯度的像素的位置，p 0是图像邻域中心的位置，高斯宽度σ设置为邻域半径的​​二分之一。

SIFT 还希望避免因单个图像梯度方向的微小变化而导致方向直方图发生较大变化。因此，它使用了一种插值技巧，将权重从单个梯度分散到相邻的方向箱中。特别是，根 bin（梯度分配给的 bin）获得 1 倍加权幅度的投票。每个相邻的 bin 获得 1 – d的投票，其中d是直方图 bin 单位与根 bin 的差异。

总的来说，SIFT 的单个图像梯度的投票是：

 在哪里∇p是bin b中像素p的梯度，wb是b的插值权重，σ是从p到中心的高斯距离。

SIFT 流水线需要相当多的步骤。HOG 稍微简单一些，但遵循许多相同的基本步骤，例如创建梯度直方图和归一化。图 8-6说明了 SIFT 架构。从原始图像中的感兴趣区域开始，我们首先将该区域划分为网格。然后将每个网格单元进一步划分为子网格。每个子网格元素包含一些像素，每个像素产生一个梯度。每个子网格元素都会产生一个加权梯度估计，其中选择权重以便子网格元素外部的梯度可以做出贡献。然后将这些梯度估计聚合到子网格的方向直方图中，其中梯度可以具有如前所述的加权投票。然后将每个子网格的方向直方图连接起来，形成整个网格的长梯度方向直方图。（如果把网格分成2×2个子网格，那么就会有4个梯度方向直方图拼接成1个。) 这是网格的特征向量，然后经过归一化-阈值-归一化过程。首先，向量被归一化为具有单位范数。然后，将各个值限制为最大阈值。最后，阈值向量再次归一化。这是图像补丁的最终 SIFT 特征描述符。

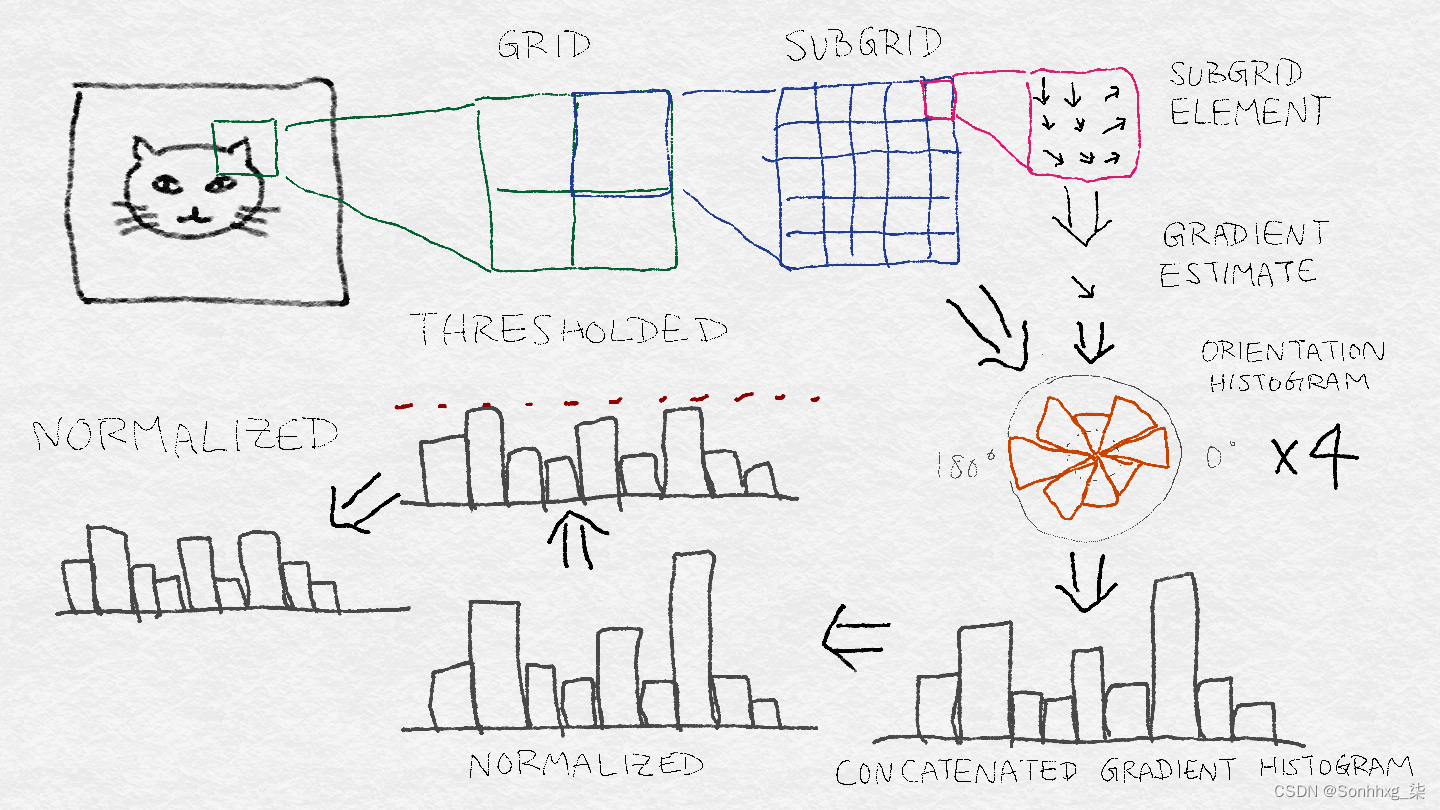
图 8-6。SIFT 架构——为原始图像中的感兴趣区域生成特征向量的步骤

所有神经网络的核心都是输入的线性函数。我们在第 4 章中遇到的逻辑回归是神经网络的一个例子。一个完全连接的神经网络只是所有输入特征的一组线性函数。回想一下，线性函数可以写成输入特征向量和权重向量之间的内积，再加上一个可能的常数项。线性函数的集合可以表示为矩阵向量乘积，其中权重向量变为权重矩阵 ( W )。

全连接层的数学定义是：

其中W的每一行都是一个权重向量，它将整个输入向量x映射到z中的单个输出。b是标量向量，表示每个神经元的常数偏移量（或偏差）。

全连接层之所以这样命名，是因为每个输入都可以用于每个输出。从数学上讲，这意味着矩阵W中的值没有限制。（正如我们很快就会看到的，卷积层对每个输出仅使用输入的一小部分。）在图形上，一个完全连接的神经网络可以用一个完整的二分图表示，其中输入中的每个节点都连接到每个节点在输出中（见图 8-7）。

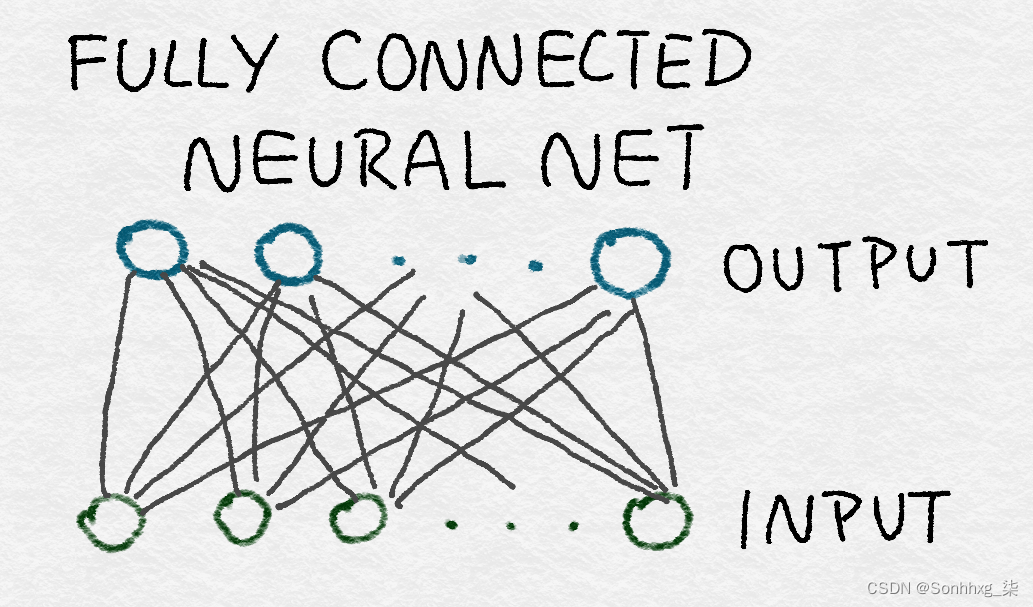
图 8-7。一个完全连接的神经网络，表示为图形

全连接层包含最大可能数量的参数（#input × #output）——因此，它们被认为是昂贵的。这种密集连接允许网络检测可能涉及所有输入的全局模式。因此，AlexNet 的最后两层是全连接的。输出仍然彼此独立，以输入为条件。

卷积层

与全连接层不同，卷积层的每个输出仅使用输入的一个子集。  转换在输入中“移动”，一次使用几个特征产生输出。为简单起见，可以对不同的输入集使用相同的权重，而不是为每组输入学习新的权重。

从数学上讲，卷积运算符将两个函数作为输入并产生一个函数作为输出。它翻转一个输入函数，将其移过另一个函数，并输出每个点的相乘曲线下的总面积：

 计算曲线下总面积的方法是取其积分。运算符在输入中是对称的，这意味着我们翻转第一个输入还是第二个输入并不重要；输出是一样的。

当我们查看图像梯度（“图像梯度”）时，我们已经看到了简单卷积的示例。但是卷积的数学定义可能仍然显得有些复杂。它的疯狂是有原因的。使用信号处理中的示例最容易解释卷积背后的直觉。

想象一下，我们有一个小黑盒子。为了查看黑匣子的作用，我们将一个刺激单元传递给它。我们将输出结果记录在一张小纸上。我们等到对原始刺激不再有反应。随着时间的推移产生的函数是响应函数；我们称它为g ( t )。

想象一下，现在我们有一些疯狂的信号f ( t )，我们继续将其馈入黑匣子。在时间t = 0 时，f (0) 与黑盒交互并产生f (0) 乘以g (0)。在时间t = 1 时，f (1) 进入黑盒并乘以g (0)。同时，黑盒继续响应之前的信号f (0)，现在乘以g (1)。因此，时间t = 1 时的总输出为 ( f (0) * g (1)) + ( f (1) * g(0))。在时间t = 2 时，情况变得更加复杂，f (2) 进入画面，f (0) 和f (1) 继续生成它们的响应。在时间t = 2的总输出是 ( f (0) * g (2)) + ( f (1) * g (1)) + ( f (2) * g (0))。通过这种方式，响应函数有效地及时翻转，τ = 0 始终与当前进入黑盒的任何内容交互，而响应函数的尾部与之前进入的任何内容交互。

图 8-8说明了每个时间步的数量（请注意，为了便于描述，我们将时间离散化——实际上，时间是连续的，所以总和实际上是一个积分）。在计算特定时间步长的卷积值时，将重叠信号相乘并求和。

图 8-8。两个离散信号 f 和 g 的卷积

这个黑盒子被称为线性系统，因为它没有做比标量乘法和求和更疯狂的事情。卷积运算符清楚地捕获了线性系统的效果。

在我们的示例中，g ( t ) 用于表示响应函数，f ( t ) 表示输入。但是由于卷积是对称的，所以哪个是响应和哪个输入并不重要。这输出只是两者的组合。g ( t ) 也称为滤波器。1个

图像是二维信号，所以我们需要一个二维滤波器。二维卷积滤波器通过对两个变量进行积分来扩展一维情况：

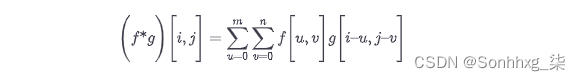
 由于数字图像具有离散像素，因此卷积积分成为离散和。此外，由于像素的数量是有限的，所以过滤函数只需要有限数量的元素。在图像处理中，二维卷积滤波器也称为内核或掩码。

将卷积过滤器应用于图像时，不一定定义覆盖整个图像的巨大过滤器。相反，人们制定了一个仅覆盖几个像素乘几个像素的小过滤器，并在整个图像上应用相同的过滤器，在水平和垂直像素方向上移动（见图 8-9）。

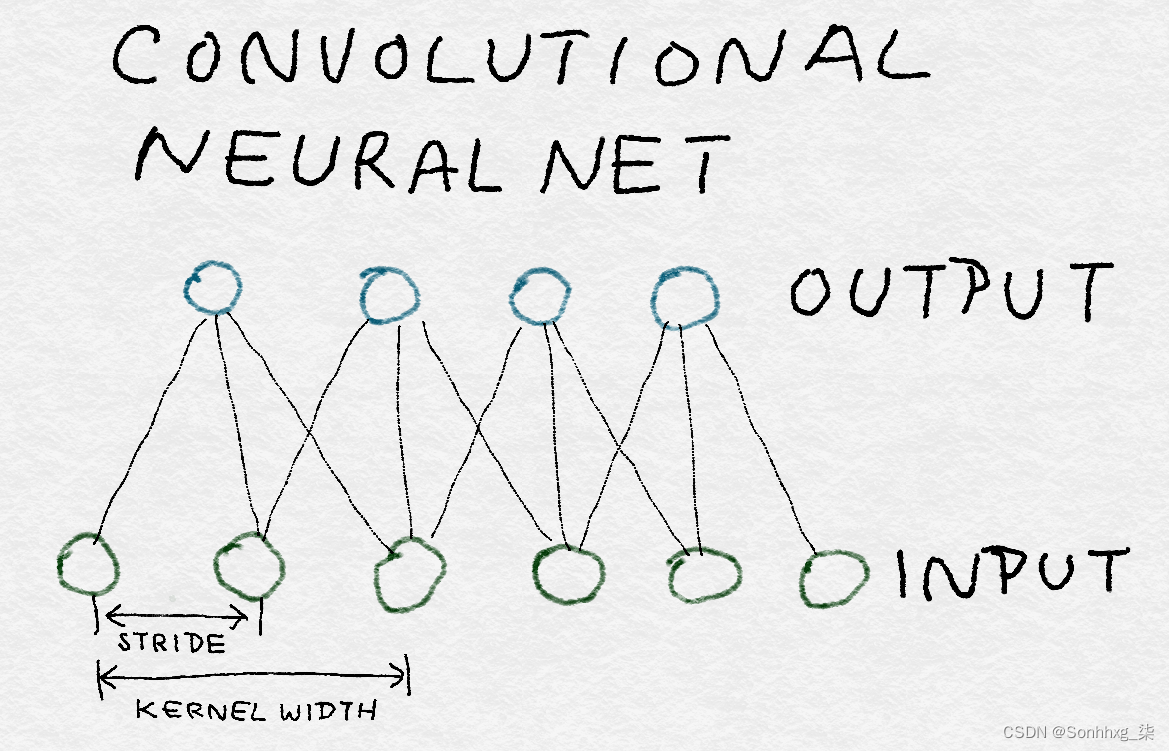
图 8-9。一维卷积神经网络的结构

 因为在整个图像中使用相同的过滤器，所以只需要定义一小组参数。权衡是过滤器一次只能吸收小像素邻域内的信息。换句话说，卷积神经网络识别局部模式而不是全局模式。

卷积滤波器示例

在此示例中，我们将高斯滤波器应用于图像。  高斯函数在零附近形成一个平滑且对称的丘。滤波器产生附近函数值的加权平均值。当应用于图像时，它具有模糊附近像素值的效果。二维高斯滤波器定义为：

 其中σ是高斯函数的标准差，它控制着“土丘”的宽度。

在示例 8-2中，我们将首先创建一个 2D 高斯滤波器，然后将其与我们最喜欢的猫图像进行卷积以生成模糊的猫（见图 8-10）。请注意，这不是计算高斯滤波器的最准确方法，但它是最容易理解的。更好的实现是采用每个离散点的加权平均值，而不是简单的点估计。

示例 8-2。在图像上应用简单的高斯滤波器

>>> import numpy as np

# First create X,Y meshgrids of size 5x5 on which we compute the Gaussian
>>> ind = [-1., -0.5, 0., 0.5, 1.]
>>> X,Y = np.meshgrid(ind, ind)
>>> X
array([[-1. , -0.5,  0. ,  0.5,  1. ],
       [-1. , -0.5,  0. ,  0.5,  1. ],
       [-1. , -0.5,  0. ,  0.5,  1. ],
       [-1. , -0.5,  0. ,  0.5,  1. ],
       [-1. , -0.5,  0. ,  0.5,  1. ]])

# G is a simple, unnormalized Gaussian kernel where the value at (0,0) is 1.0
>>> G = np.exp(-(np.multiply(X,X) + np.multiply(Y,Y))/2)
>>> G
array([[ 0.36787944,  0.53526143,  0.60653066,  0.53526143,  0.36787944],
       [ 0.53526143,  0.77880078,  0.8824969 ,  0.77880078,  0.53526143],
       [ 0.60653066,  0.8824969 ,  1.        ,  0.8824969 ,  0.60653066],
       [ 0.53526143,  0.77880078,  0.8824969 ,  0.77880078,  0.53526143],
       [ 0.36787944,  0.53526143,  0.60653066,  0.53526143,  0.36787944]])

>>> from skimage import data, color
>>> cat = color.rgb2gray(data.chelsea())

>>> from scipy import signal
>>> blurred_cat = signal.convolve2d(cat, G, mode='valid')

>>> import matplotlib.pyplot as plt
>>> fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,4), 
...                                sharex=True, sharey=True)

>>> ax1.axis('off')
>>> ax1.imshow(cat, cmap=plt.cm.gray)
>>> ax1.set_title('Input image')
>>> ax1.set_adjustable('box-forced')

>>> ax2.axis('off')
>>> ax2.imshow(blurred_cat, cmap=plt.cm.gray)
>>> ax2.set_title('After convolving with a Gaussian filter')
>>> ax2.set_adjustable('box-forced')

图 8-10。应用 2D 高斯滤波器之前和之后的猫图像

卷积的AlexNet 中的层是三维的。换句话说，它们对上一层的体素（数组中表示图像的 3D 空间的值）进行操作。第一个卷积神经网络获取原始 RGB 图像并学习所有三个颜色通道的局部图像邻域的卷积滤波器。后续层将跨越空间和内核维度的输入体素作为输入。有关详细信息，请参见图 8-14 。

整流线性单元 (ReLU) 变换

的输出神经网络经常通过另一种非线性变换，也称为激活函数。常见的选择是tanh函数（介于 –1 和 1 之间的平滑非线性函数）、sigmoid函数（介于 0 和 1 之间的平滑非线性函数，在“逻辑回归分类”中介绍），或所谓的整流线性单元。ReLU 是线性函数的简单变体其中负数部分被清零。换句话说，它会去除负值，但保留正数部分不受限制。ReLU 的范围从 0 延伸到 ∞。

常用激活函数

ReLU 是负数部分归零的线性函数：

ReLU( x ) = max(0, x )

tanh 函数是一个从 –1 平滑增加到 1 的三角函数：

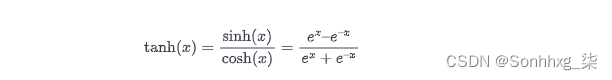
 sigmoid 函数从 0 平滑地增加到 1：

 这三个函数如图 8-11 所示。

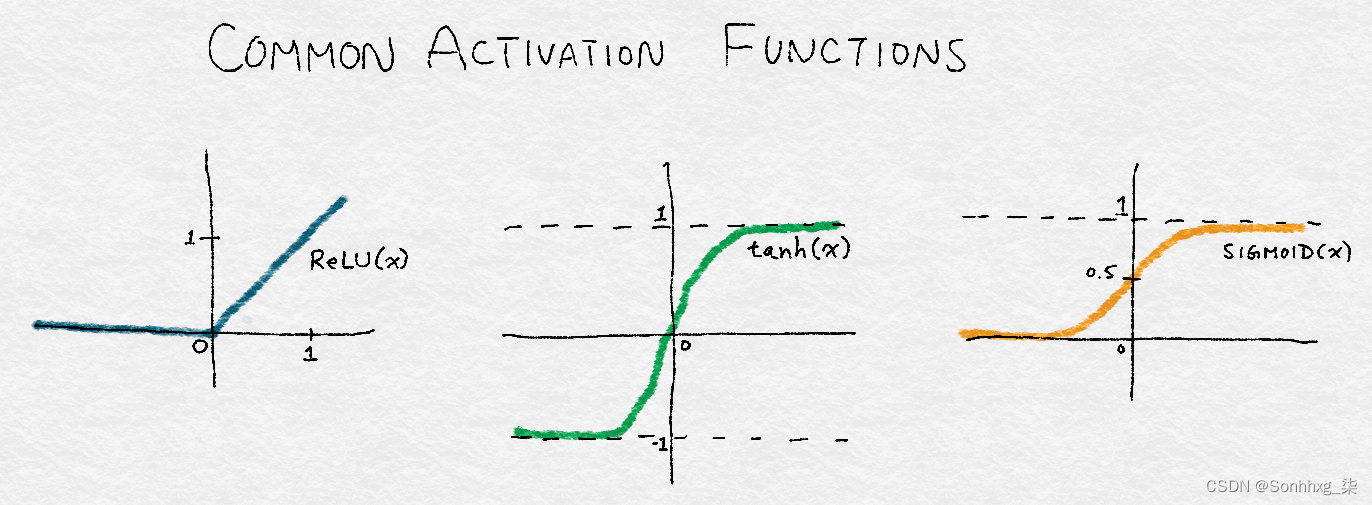
图 8-11。三种常见激活函数的图示：RELU、TANH 和SIGMOID

ReLU 变换对原始图像或高斯滤波器等非负函数没有影响。然而，经过训练的神经网络，无论是完全连接的还是卷积的，都可能输出负值。AlexNet 使用 ReLU 而不是其他转换，理由是训练期间收敛速度更快（Krizhevsky 等人，2012 年）。它将 ReLU 应用于每个卷积层和全连接层。

在第 4章和本章前面的讨论之后，归一化现在应该是一个熟悉的概念。归一化将单个输出除以集体总响应的函数。因此，理解规范化的另一种方式是它创建邻居之间的竞争，因为每个输出的强度现在是相对于它的邻居来衡量的（见图 8-12）。AlexNet 对不同内核的每个位置的输出进行标准化。

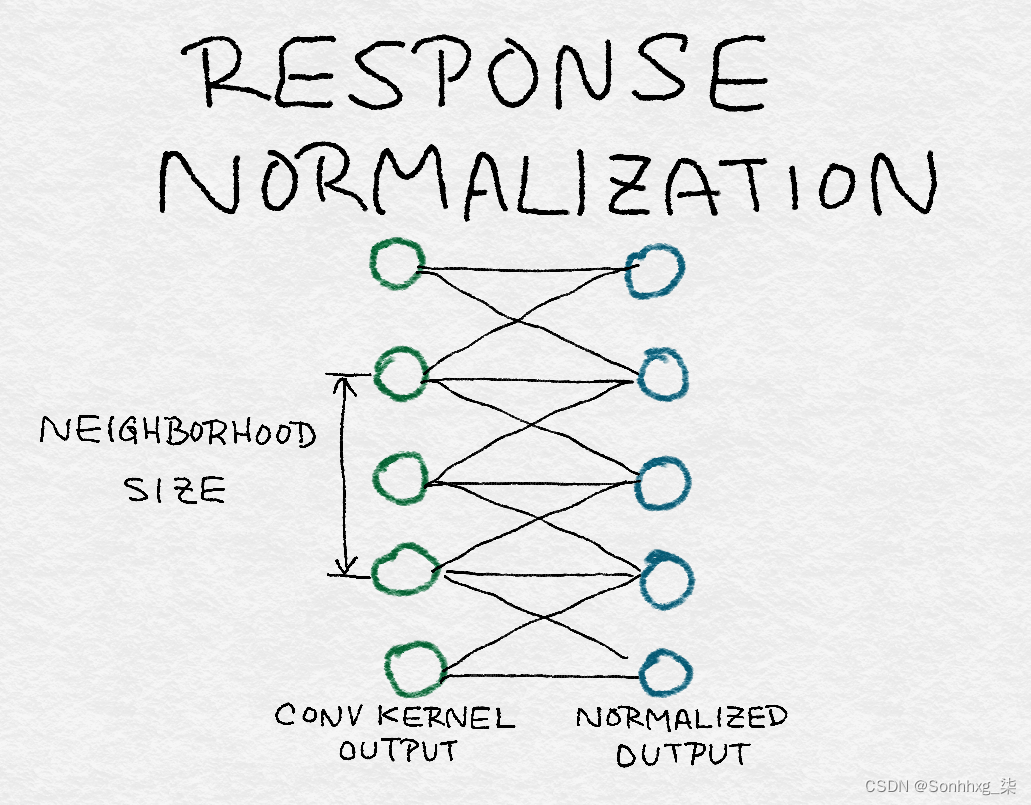
图 8-12。前一层卷积核输出的响应归一化结构——归一化常数是根据前一层的邻域计算的

本地响应规范化导致相邻内核之间的竞争

顾名思义，局部响应归一化将一个值除以其邻居的组合。这是公式：

 这里，xk是第k个内核的输出，yk是相对于邻域中其他内核的归一化响应。标准化是针对每个输出位置单独执行的。也就是说，对于每个输出位置 ( i , j )，我们对附近的卷积核输出进行归一化。请注意，这与对图像邻域或输出位置进行归一化不同。核邻域的大小c、α和β都是通过图像验证集调整的超参数。

池化层

池化层将多个输入组合成一个输出。当卷积滤波器在图像上移动时，它会为其镜头下的每个邻域生成一个输出。池化迫使局部图像邻域产生一个值而不是多个值。这减少了深度学习网络中间层的输出数量，有效降低了网络对训练数据过拟合的概率。

有多种方法可以汇集输入：平均、求和（或计算广义范数）或取最大值。池化在图像或中间输出层上移动。AlexNet 使用重叠最大池化，以两个像素（或输出）的步幅在图像上移动，并在三个相邻像素之间进行池化。

图 8-13。最大池化使用非线性下采样输出每个子区域的最大非重叠矩形数

AlexNet的结构

总之，AlexNet 涉及五个卷积层、两个响应归一化层、三个最大池化层和两个完全连接层。结合最终的分类输出层，模型中共有13个神经网络层，形成8个层组。详情见图 8-14。

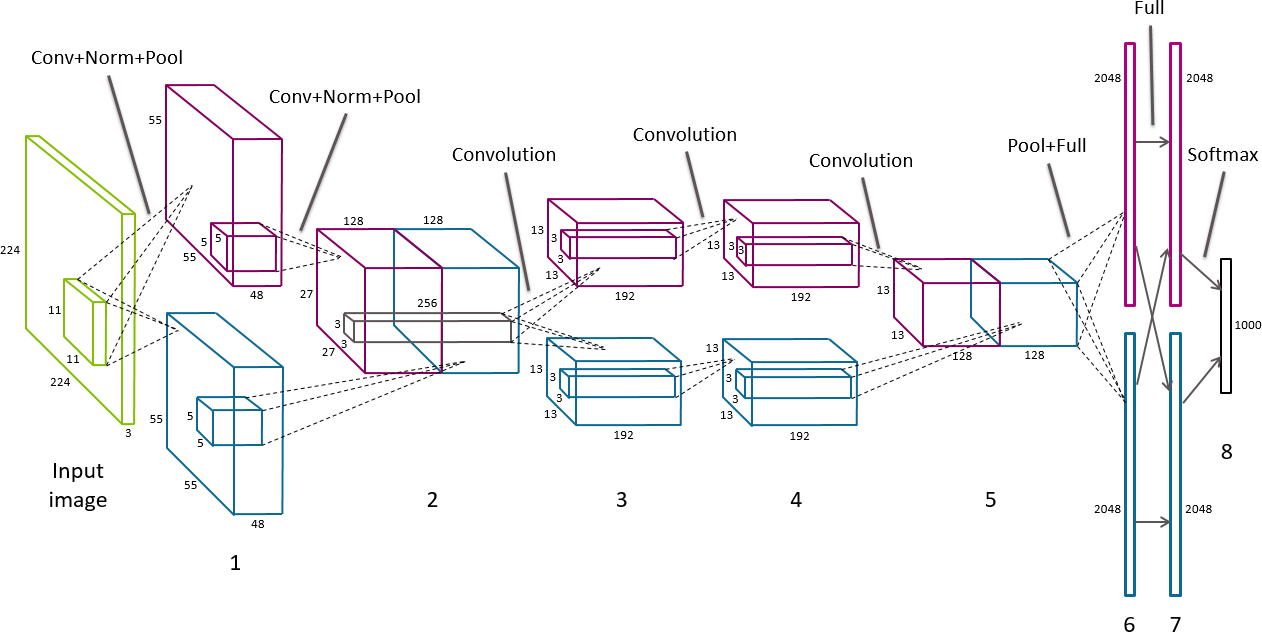
图 8-14。AlexNet 的架构图——不同深浅的灰色（或品红色和蓝色，如果您正在查看彩色插图）表示驻留在 GPU 1 和 GPU 2 上的层

输入图像首先缩放为 256 × 256 像素。输入实际上是大小为 224 × 224 的随机裁剪，具有 3 个颜色通道。前两个卷积层之后分别是响应归一化层和最大池化层，最后一个卷积层之后是最大池化层。原始论文将训练数据和计算拆分到两个 GPU 上。层之间的通信主要限于同一 GPU 内。例外情况是层组 2 和 3 之间，以及层组 5 之后。在这些边界点，下一层将跨两个 GPU 的前一层的内核体素作为输入。ReLU 转换遵循每个中间层。

图 8-15显示了卷积+响应归一化+最大池化的详细视图。请注意，归一化常数是跨内核计算的，而池化是跨图像区域进行的。此外，池化减少了层的维度。

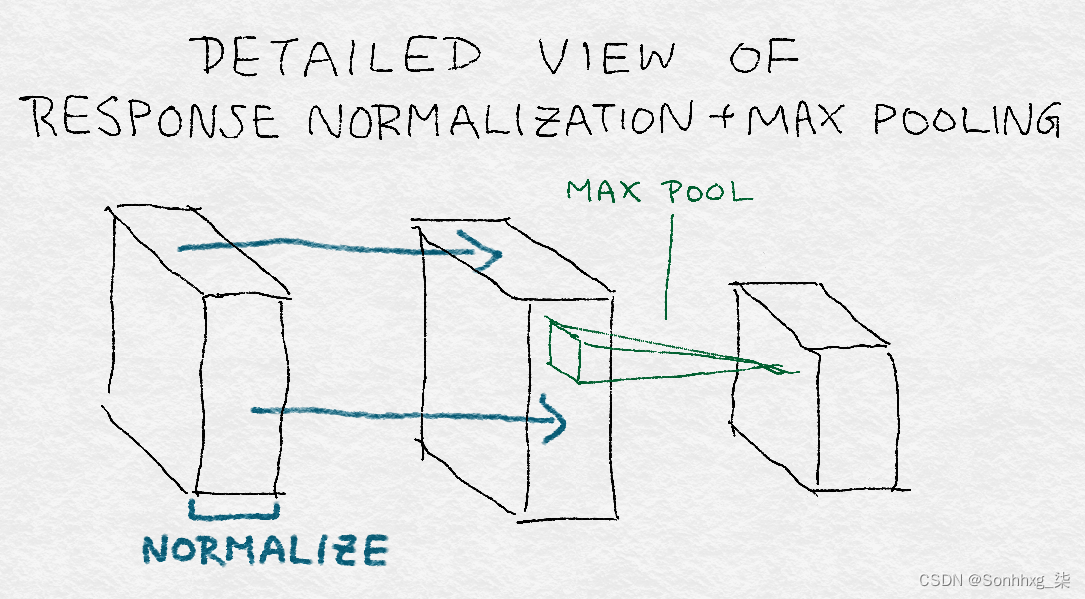
图 8-15。卷积+响应归一化+最大池化详解

请注意，AlexNet 的架构让人想起 SIFT/HOG 特征提取器的梯度直方图-归一化-阈值-归一化架构（见图 8-6），但具有更多层。（因此“深度学习”中的“深度”。）然而，与 SIFT/HOG 不同的是，卷积核和全连接权重是从数据中学习的，而不是预定义的。此外，SIFT 中的归一化步骤是在整个图像区域的特征向量上执行的，而 AlexNet 中的响应归一化层是在卷积核上归一化的。

在较高层次上，该模型首先从局部图像邻域中提取模式。每个后续层都建立在前一层的输出之上，有效地覆盖了原始图像的连续更大区域。因此，即使前五个卷积层都具有相当小的内核宽度，后面的层也能够形成更多的全局模式。最后的全连接层是最全局的。

尽管模式的要点在概念上很清楚，但要将每一层挑选出的实际模式可视化是一个难题。图8-16和8-17显示了模型学习的前两层卷积核的可视化。第一层由不同方向的灰度边缘和纹理检测器以及颜色斑点和纹理组成。第二层似乎包含各种平滑模式的检测器。

图 8-16。经过训练的 AlexNet 中第一层卷积核的可视化：前半部分核是在 GPU 1 上学习的，似乎可以检测不同方向的灰度边缘和纹理；下半部分，在第二个 GPU 上训练，专注于颜色斑点和图案

图 8-17。经过训练的AlexNet的第二层卷积核的可视化

尽管该领域取得了巨大进步，但图像特征化仍然更像是一门艺术而非科学。十年前，人们结合使用图像梯度、边缘检测、方向、空间线索、平滑和归一化来手工制作特征提取步骤。如今，深度学习架构师构建的模型封装了很多相同的想法，但参数是从训练图像中自动学习的。魔法巫术还在，只是在模型中隐藏了一个更深的抽象！