数据结构与算法——查找算法

本文将不断更新查找有关算法，由于精力有限，因此本博文将分多次更新，感谢您的关注

文章目录

数据结构与算法——查找算法
- 1. 二分法查找（折半查找）
- - 1.1 算法叙述
  - 1.2 实例说明
- 2. 插值查找（比例查找）
- - 2.1 算法叙述
  - 2.2 实例说明
- 3. 斐波那契查找（黄金分割法查找）
- - 3.1 算法叙述
  - 3.2 实例说明
- 4. 线性索引查找
- - 4.1 算法叙述
  - 4.2 实例说明

1. 二分法查找（折半查找）

1.1 算法叙述

二分法查找又称折半查找，顾名思义也就是将待查找范围不断折半直到不能再折为止
适用范围：数据表是顺序结构，也就是从小到大或从大到小已经排好序
算法复杂度：O(logn)
思路如下图：

1.2 实例说明

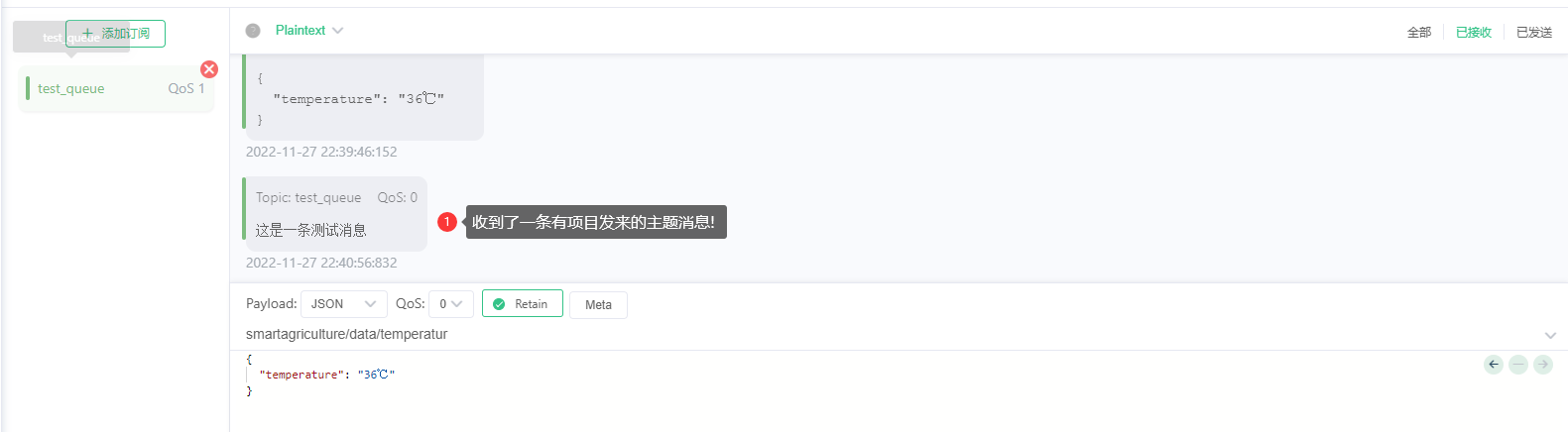
以NTC温度转化为例，通过ADC采集到NTC的电压之后，计算出NTC的电阻值，之后采用查表的方案查询此NTC阻值所对应的温度
本文已 TSM1A682J3952RZ 这颗NTC电阻为例，数据手册地址：NTC数据手册地址
代码如下：
- temperature 内记录了从数据手册内获取到的NTC从 -40 ~ 125℃ 所对应的阻值
- sort_dichotomy 为二分法查找算法实现

#include <stdio.h>

/* ntc -40 ~ 125℃ 阻值 */
const float temperature[] = {
    249.76, 233.36, 218.16, 204.07, 190.98, 178.8, 167.47, 156.9, 147.06, 137.88,
    129.31, 121.31, 113.85, 106.88, 100.38, 94.3, 88.626, 83.325, 78.372, 73.743,
    69.417, 65.372, 61.589, 58.05, 54.738, 51.638, 48.735, 46.015, 43.466, 41.075,
    38.833, 36.729, 34.753, 32.897, 31.153, 29.513, 27.97, 26.518, 25.151, 23.863,
    22.649, 21.505, 20.426, 19.407, 18.445, 17.537, 16.679, 15.868, 15.101, 14.375,
    13.688, 13.039, 12.423, 11.84, 11.288, 10.765, 10.269, 9.7981, 9.3517, 8.9281,
    8.5261, 8.1445, 7.7821, 7.4379, 7.1108, 6.8, 6.5046, 6.2237, 5.9565, 5.7024,
    5.4606, 5.2305, 5.0115, 4.8029, 4.6043, 4.4151, 4.2348, 4.063, 3.8992, 3.743,
    3.594, 3.4519, 3.3163, 3.1869, 3.0633, 2.9453, 2.8326, 2.7249, 2.6219, 2.5235,
    2.4294, 2.3394, 2.2533, 2.1709, 2.0921, 2.0166, 1.9442, 1.8749, 1.8086, 1.7449,
    1.6839, 1.6254, 1.5693, 1.5154, 1.4637, 1.4141, 1.3664, 1.3207, 1.2767, 1.2344,
    1.1938, 1.1548, 1.1172, 1.0811, 1.0463, 1.0128, 0.98063, 0.94961, 0.91974, 0.89097,
    0.86325, 0.83654, 0.81079, 0.78596, 0.76202, 0.73894, 0.71667, 0.69518, 0.67444, 0.65443,
    0.63512, 0.61647, 0.59846, 0.58107, 0.56427, 0.54804, 0.53237, 0.51722, 0.50258, 0.48843,
    0.47475, 0.46153, 0.44875, 0.43639, 0.42443, 0.41288, 0.4017, 0.39089, 0.38043, 0.37031,
    0.36052, 0.35105, 0.34189, 0.33303, 0.32445, 0.31616, 0.30813, 0.30035, 0.29284, 0.28556,
    0.27852, 0.2717, 0.26511, 0.25873, 0.25255, 0.24658
};

/**
 * @brief 二分法查找算法
 * 
 * @param elem 待查找数据
 * @param table 数据表
 * @param table_size 数据表大小
 * @return int -1：参数错误 >=0：待查找元素所在表中位置
 */
int sort_dichotomy(float elem, const float *table, int table_size)
{
    int mid = 0, left = 0, right = 0;

    if (table == NULL || table_size == 0)
        return -1;

    left = 0;
    right = table_size - 1;
    mid = (left + right) / 2;

    if (elem > table[0])
    {
        return 0;
    }
    else if (elem < table[table_size - 1])
    {
        return right;
    }

    while (left < right)
    {
        if (elem > table[mid])
        {
            right = mid;
            mid = (left + right) / 2;
        }
        else if (elem < table[mid])
        {
            left = mid;
            mid = (left + right) / 2;
        }
        else if (elem == table[mid])
        {
            break;
        }

        if (left == mid)
        {
            break;
        }
        else if (right == mid)
        {
            mid += 1;
            break;
        }
    }

    printf("mid:%d left:%d right:%d\n", mid, left, right);

    return mid;
}

int main(int argc, char **argv)
{
    printf("*************************\n");
    printf("二分法排序\n");
    printf("*************************\n");

    int temp = 0;
    temp = sort_dichotomy(17.5f, temperature, sizeof(temperature));
    temp -= 40;
    printf("temperature is:%d\n", temp);

    return 0;
}