循环神经网络(part 2) - 梯度爆炸实验

写在开头

经过前面的实验我们不难发现，我们所构建的简单神经网络，对于较短的序列预测效果尚佳，但是应对起长的序列效果却一塌糊涂。对此，就不得不说简单循环神经网络对于长程依赖问题效果不好的两大原因：梯度爆炸和梯度消失。

解决方式概览

• 对于梯度爆炸问题：我们通过权重衰减或者梯度截断能够较好地避免；
• 对于梯度消失问题：由于模型存在的故有问题，我们可以通过改变模型，如使用长短期记忆网络LSTM来进行缓解。

梯度爆炸实验

本次实验，我们将复现梯度爆炸的问题，然后尝试使用梯度截断的方式进行解决。
采用长度为20的数据集进行实验，并在训练过程中输出$W,U,b$的梯度向量的范数来衡量梯度变化情况。

梯度打印函数

在训练过程中打印梯度，分别定义W_list，U_list和b_list，用于存储前面所说的梯度向量的范数。代码如下：

W_list, U_list, b_list = [], [], []

def display_gvec(model):
    grad_w_l2, grad_u_l2, grad_b_l2 = 0., 0., 0.
    for name, param in model.named_parameters():
        if name == "rnn_model.W":
            grad_w_l2 = torch.norm(param.grad, p=2).numpy()
        if name == "rnn_model.U":
            grad_u_l2 = torch.norm(param.grad, p=2).numpy()
        if name == "rnn_model.b":
            grad_b_l2 = torch.norm(param.grad, p=2).numpy()
    print(f"grad_w_l2: {grad_w_l2:.5f}, grad_u_l2: {grad_u_l2:.5f}, grad_b_l2: {grad_b_l2:.5f} ")
    W_list.append(grad_w_l2)
    U_list.append(grad_u_l2)
    b_list.append(grad_b_l2)

思考：什么是范数、L2范数、为什么要打印梯度范数

L2和L-P范数定义如下：
$$\begin{gathered} L_2=||x|{|}_2=(\sum _i|x_i{|}^2{)}^{1/2} \\ {L}_P=||x|{|}_P=(\sum _i|x_i{|}^P{)}^{1/P} \end{gathered}$$

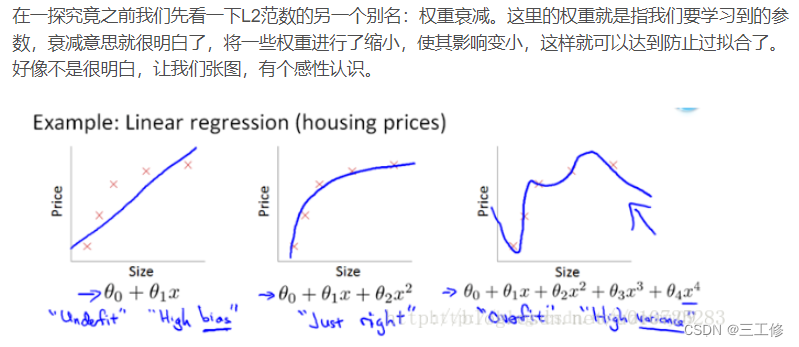
这边推荐一个博客写的非常好：传送门：一文搞懂深度学习正则化的L2范数

至于为什么要打印L2范数，个人觉得是因为L2范数对于参数数值变化更为直观清晰。

复现梯度爆炸现象

为了更好地复现梯度爆炸问题，使用SGD优化器将批大小和学习率调大，设置学习率为0.2，同时计算交叉熵损失时reduction设置为sum，表示将损失进行累加。
获取训练过程中关于W，U和b参数梯度的L2范数，并将其绘制为图片。

• 选取Tanh函数，因为其饱和区导数接近于0。由于梯度的急剧变化，参数数值变的较大或较小，容易落入梯度饱和区，导致梯度为0，模型很难继续训练。

代码如下：

num_epochs = 20
lr = 0.2
num_digits = 10
input_size = 32 # 将数字映射为向量的维度
hidden_size = 32 # 隐状态向量的维度
num_classes = 19
batch_size = 64
save_dir = "./checkpoints"

length = 20
print(f"\n====> Training SRN with data of length {length}.")

# 加载长度为length的数据
data_path = f"E:/nndl/misc/datasets/{length}"
train_examples, dev_examples, test_examples = load_data(data_path)
train_set, dev_set, test_set = DigitSumDataset(train_examples), DigitSumDataset(dev_examples),DigitSumDataset(test_examples)
train_loader = DataLoader(train_set, batch_size=batch_size)
dev_loader = DataLoader(dev_set, batch_size=batch_size)
test_loader = DataLoader(test_set, batch_size=batch_size)
# 实例化模型
base_model = SRN(input_size, hidden_size)
model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
# 指定优化器
optimizer = torch.optim.SGD(model.parameters(),lr)
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = nn.CrossEntropyLoss(reduction="sum")

# 基于以上组件，实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)

# 进行模型训练
model_save_path = os.path.join(save_dir, f"srn_explosion_model_{length}.pdparams")
runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=1,
             save_path=model_save_path, additional={"grads l2 value ":display_gvec})

我们将训练时的梯度用matplotlib打印出来，结果如下：

在测试集上的结果如下：

使用梯度截断解决梯度爆炸问题

梯度截断是一种可以有效解决梯度爆炸问题的启发式方法，当梯度的模大于一定阈值时，将它截断为一个较小的数。一般有两种截断方式：按值截断和按模截断。本实验使用按模截断的方式解决梯度爆炸问题(Pascanu et al., 2013a)。公式如下：

其中 v 是范数上界，g 用来更新参数。因为所有参数（包括不同的参数组，如权重
和偏置）的梯度被单个缩放因子联合重整化，所以后一方法具有的优点是保证了每
个步骤仍然是在梯度方向上的，但实验表明两种形式类似。虽然参数更新与真实梯
度具有相同的方向梯度，经过梯度范数截断，参数更新的向量范数现在变得有界。这种有界梯度能避免执行梯度爆炸时的有害一步。
在torch中，我们使用torch.nn.utils.clip_grad_norm_函数即可进行梯度截断。其代码如下：

import warnings
import torch
from torch._six import inf
from typing import Union, Iterable
_tensor_or_tensors = Union[torch.Tensor, Iterable[torch.Tensor]]
def clip_grad_norm_(
        parameters: _tensor_or_tensors, max_norm: float, norm_type: float = 2.0,
        error_if_nonfinite: bool = False) -> torch.Tensor:
    r"""Clips gradient norm of an iterable of parameters.

    The norm is computed over all gradients together, as if they were
    concatenated into a single vector. Gradients are modified in-place.

    Args:
        parameters (Iterable[Tensor] or Tensor): an iterable of Tensors or a
            single Tensor that will have gradients normalized
        max_norm (float or int): max norm of the gradients
        norm_type (float or int): type of the used p-norm. Can be ``'inf'`` for
            infinity norm.
        error_if_nonfinite (bool): if True, an error is thrown if the total
            norm of the gradients from :attr:`parameters` is ``nan``,
            ``inf``, or ``-inf``. Default: False (will switch to True in the future)

    Returns:
        Total norm of the parameter gradients (viewed as a single vector).
    """
    if isinstance(parameters, torch.Tensor):
        parameters = [parameters]
    grads = [p.grad for p in parameters if p.grad is not None]
    max_norm = float(max_norm)
    norm_type = float(norm_type)
    if len(grads) == 0:
        return torch.tensor(0.)
    device = grads[0].device
    if norm_type == inf:
        norms = [g.detach().abs().max().to(device) for g in grads]
        total_norm = norms[0] if len(norms) == 1 else torch.max(torch.stack(norms))
    else:
        total_norm = torch.norm(torch.stack([torch.norm(g.detach(), norm_type).to(device) for g in grads]), norm_type)
    if error_if_nonfinite and torch.logical_or(total_norm.isnan(), total_norm.isinf()):
        raise RuntimeError(
            f'The total norm of order {norm_type} for gradients from '
            '`parameters` is non-finite, so it cannot be clipped. To disable '
            'this error and scale the gradients by the non-finite norm anyway, '
            'set `error_if_nonfinite=False`')
    clip_coef = max_norm / (total_norm + 1e-6)
    # Note: multiplying by the clamped coef is redundant when the coef is clamped to 1, but doing so
    # avoids a `if clip_coef < 1:` conditional which can require a CPU <=> device synchronization
    # when the gradients do not reside in CPU memory.
    clip_coef_clamped = torch.clamp(clip_coef, max=1.0)
    for g in grads:
        g.detach().mul_(clip_coef_clamped.to(g.device))
    return total_norm

可以很清楚的看到如上述计算过程的代码用于实现梯度截断。

引入梯度截断后，我们重新对模型进行训练，结果如下：

思考：梯度截断解决梯度爆炸问题的原理？

梯度截断可以使梯度下降在梯度爆炸的部分附近更合理地执行。将梯度看作地形图，那么梯度爆炸的地方就是一个悬崖，如果跳下去就会粉身碎骨（梯度爆炸导致的模型恶化），梯度截断则像传送门，将梯度传送到低的地方“安全着陆”。
又找到了一个描述：
通过梯度截断，可以较大程度的抑制梯度爆炸现象。如下图所示，图中曲面表
示的𝐽(𝑤, 𝑏)函数在不同网络参数 w,b 下的误差值𝐽，其中有一块区域𝐽(𝑤, 𝑏)函数的梯度变化
较大，一旦网络参数进入此区域，很容易出现梯度爆炸的现象，使得网络状态迅速恶化。
图右演示了添加梯度截断后的优化轨迹，由于对梯度进行了有效限制，使得每次更
新的步长得到有效控制，从而防止网络突然恶化。

写在最后

通过本次实验，我们了解到了在循环神经网络中一个非常需要重视的问题——梯度爆炸，在不改变模型本身大体结构的情况下，我们通过对梯度进行截断从而遏制梯度爆炸的问题。这个方法简单粗暴，但是非常好用。