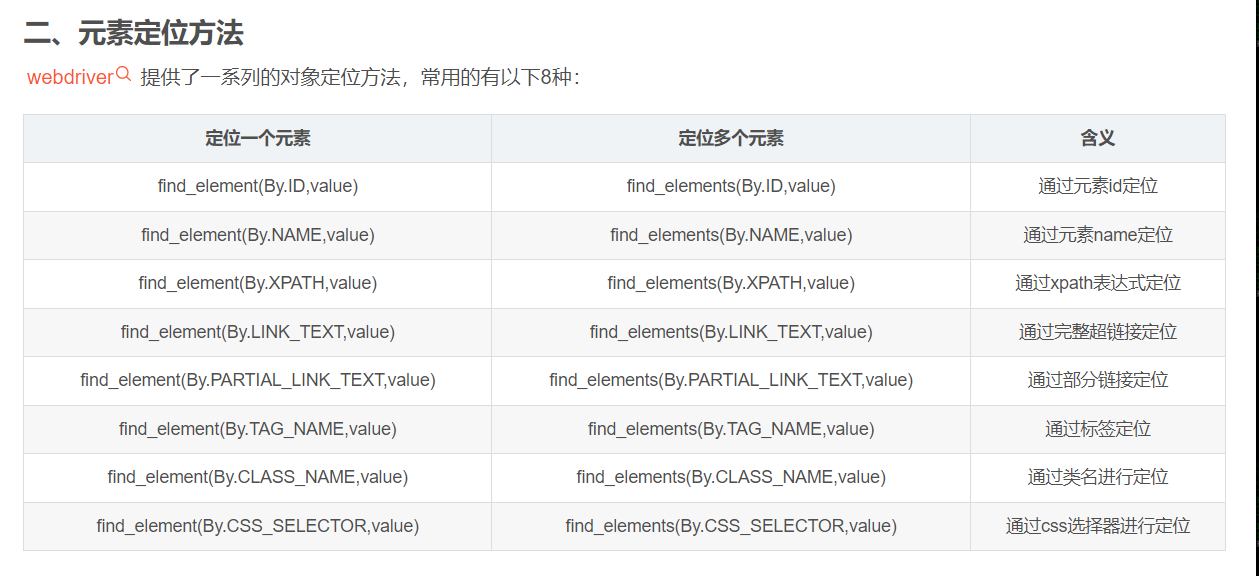
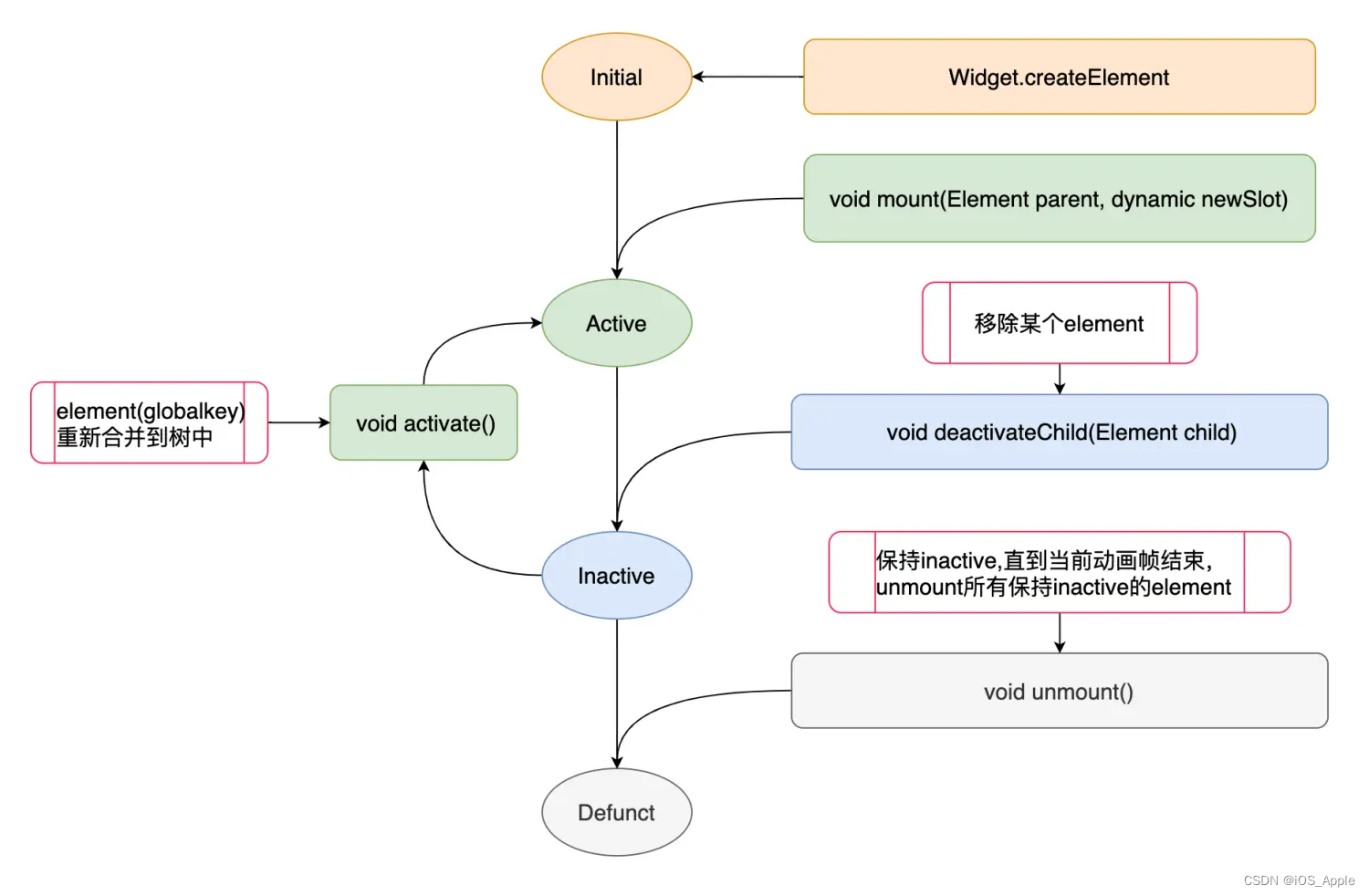
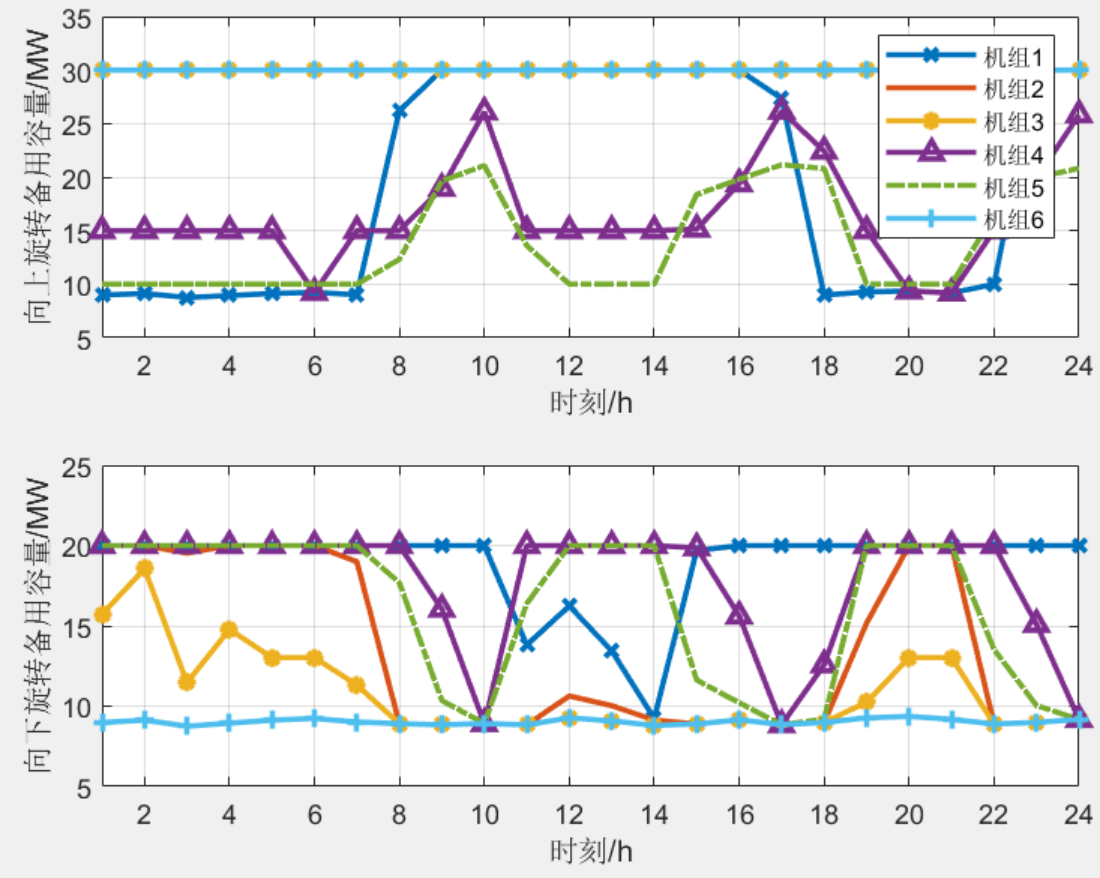
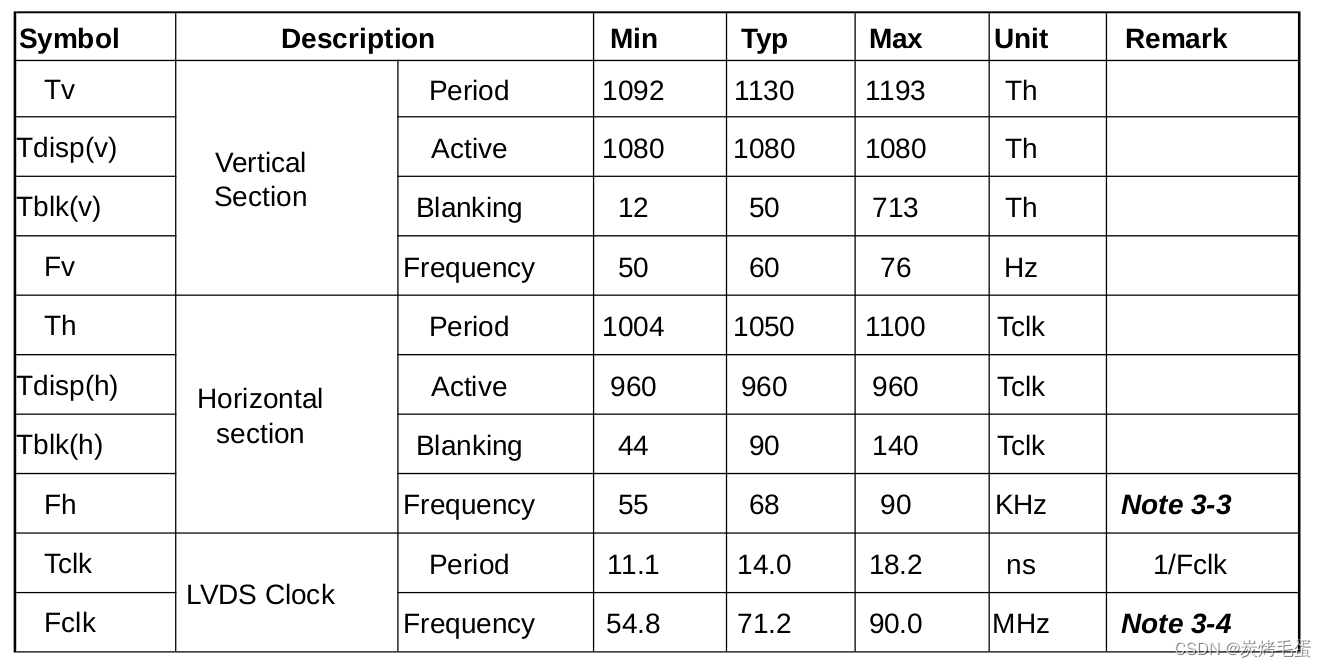
都学了递归版的快速排序为何还要再学非递归实现?由于在递归过程中,如果数据量过大,那么实现时容易导致栈溢出,虽然代码没有问题,但是就是会崩,因此要将其改为非递归来实现
文章目录
- 一、快速排序(非递归)
- 二、计数排序
一、快速排序(非递归)
如何做到将递归算法改为非递归算法?
简单的递归可以直接将其改为循环(如斐波那契),但是如果是复杂的递归算法,再直接改为循环十分复杂,而一般选用栈辅助将其改为非递归
再来回顾一下快速排序的思想。
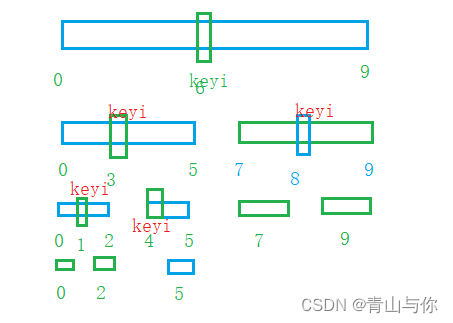
思想:在区间范围内选出一个关键字,经过单趟排序之后关键字位置左边的数据全小于或者等于它,关键字右边的数据全大于或者等于它。一趟排序将这个关键字排好了,同样也分隔出了它的左区间和右区间,再以同样的方法排它的左区间和右区间,直至区间范围为1或者不存在为止
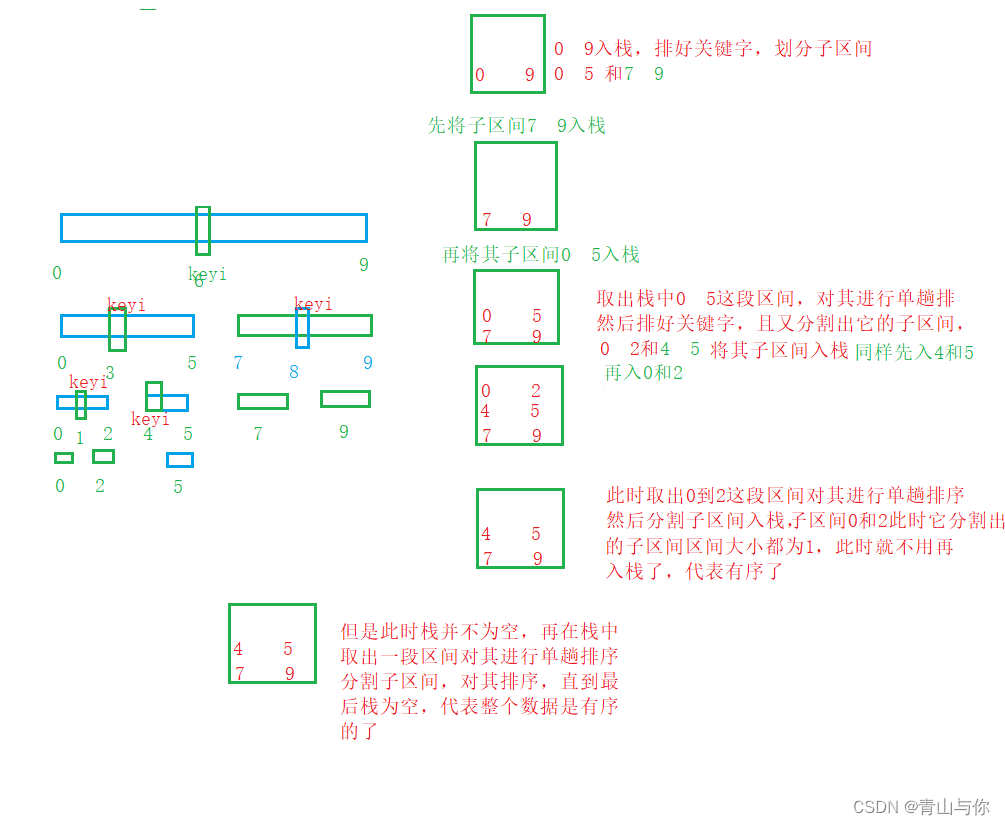
而递归实现快速排序是每次控制的是区间,每次递归调用栈都是将区间压栈,每递归一次,区间都在变化。因此用栈实现快速排序时,入栈的是区间,而由于每次递归都是先排的左区间,而栈是一种后进先出的数据结构,所以在将区间入栈时要先将右区间压栈,然后再将左区间压栈,保证每次单趟排先将左区间排好再排右区间
单趟排。排出keyi此时分隔出keyi的左右区间,然后把他的左、右区间压栈,此时又对它的左右区间进行单趟排,排出keyi,分隔左右区间,每次单趟排完后会分隔出左右区间,然后左右区间入栈,直至最后区间为1或者不存在时,就不用再入栈了。总体是:
从栈中取一段区间,进行单趟排。单趟排序后分隔子区间(左、右区间)入栈。子区间只有一个值或者不存在就不入栈了
每一次单趟排是如何排的,这里用前后指针法实现,每次单趟排好后,返回关键字所在下标
那么用栈辅助改递归,这个栈从和而来,我这里是以前写好了,保存下来的,在vs中只需要选中源文件
然后点击鼠标右键找到
找到以前保存栈实现的文件,将其拷贝
之后再点击源文件
再点击

以前是新建但是现在是点击现有,然后找到当前程序所在目录,将刚才拷贝的栈实现的文件拷贝到当前程序中即可。
前后指针法排单趟
//前后指针法
int QuickSort3(int* a, int left, int right)
{
int begin = left;
int end = right;
//随机选数,主要针对已经有序的情况,提高性能
int randi = left + (rand() % (right - left));
if (randi != left)
{
Swap(&a[randi], &a[left]);
}
int key = left;
int cur = left + 1;
int prev = left;
while (cur <= right)
{
if (a[cur] < a[key] && ++prev != cur)
{
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[key], &a[prev]);
key = prev;
return key;
}
//取区间入栈然后对其单趟排,单趟排好keyi之后分割出它的子区间,将分割出的子区间入栈,再进行单趟排,再分割子区间入栈,每次单趟排排好一个数,直至区间范围为一或者不存在
//
void QuicksortNone(int* a, int begin, int end)
{
St st;
STInit(&st);
STPush(&st, end);
STPush(&st, begin);
while (!STEmpty(&st))
{
int begin1 = STTop(&st);
STPop(&st);
int end1 = STTop(&st);
STPop(&st);
int keyi = QuickSort3(a, begin1, end1);
if (keyi + 1 < end1)
{
STPush(&st, end1);
STPush(&st, keyi+1);
}
if (keyi > begin1)
{
STPush(&st, keyi - 1);
STPush(&st, begin1);
}
}
STDestroy(&st);
}
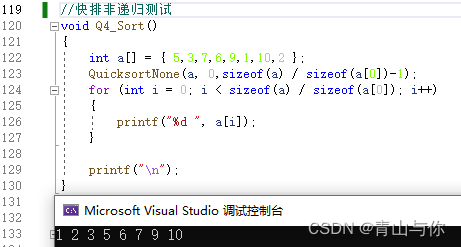
非递归快速排序时间复杂度O(nlogn),空间复杂度o(1)
二、计数排序
适用于数组存在大量重复数据且最大值和最小值之差不是特别大的情况
思想:统计数组中每个数据出现的次数,怎么统计?用一个新数组存储原数组数据出现的次数 。 这个数组如何来?当然是向内存动态申请开辟
新数组开辟多大空间合适?
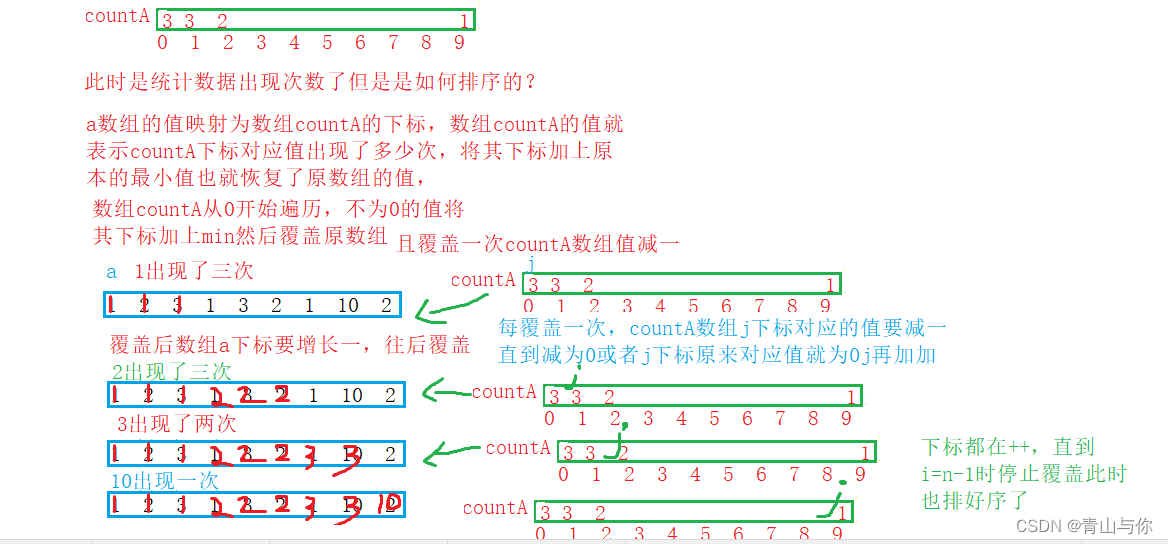
由于存的是原数组数据出现次数,那么只需要数组数据值出现一次,那么它对应值作为下标的值就加一(开辟的数组内容全部初始化为0)
只要数组中的值出现一次,那么它对应的值作为新数组下标所对应的值就加一,那么新数组范围如何确定?
其实也就是原数组最大值与最小值之差,由于用原数组值作为下标 所以先遍历一遍找出数组中的最大值和最小值,这时确定新数组开辟大小
由于存储从0开始,所以需要原数组值减去它的最小值 最后将新开辟数组的下标再加上原数组最小值就可以直接覆盖原数组,如何覆盖的?
void CountSort(int* a, int n)
{
int max = a[0], min = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;//要包含0,所以这个存储数组大小要开最大值和最小值之差再加一
//开一个数组用来统计数组数据出现的次数
int* countA = (int*)malloc(sizeof(int) * range);
if (countA == NULL)
{
perror("ocuntA fail\n");
return;
}
//将新开的这个数组内容全部都初始化为0
//由于它存储的内容是原数组数据出现的次数
memset(countA, 0, sizeof(int) * range);//c语言内置库函数将每个字节都初始化为0
//以原数组中的数据作为新开数组的下标,然后统计它出现的次数
//由于原数组最小值很可能不是从0开始
//而新数组要从0开始存储
//所以新数组下标是a[i] - min这个表达式
for (int i = 0; i < n; i++)
{
//将原数组内容它对应的数字为countA下标加加,即数组对应数据在数组中出现的次数
countA[a[i]-min]++;
}
int j = 0;
for (int i = 0; i < n; )//i<n后面的调整不可再加,原因是下面加了,如果再加会造成越界
{
//可以在这里做出调整,将其i--,但是这里多此一举
while (countA[j]--)
{
a[i++] = j + min;
}
j++;
}
free(countA);
}

计数排序时间复杂度为O(n+range)当range<n时,时间复杂度为O(n),空间复杂度为O(range),但是它的条件十分苛刻,需要很多重复数据且这些数据最大值和最小值之差不可过大,所以在现实生活中很少用到,但是在有些场景下会用到,所以还是值得一学,毕竟时间复杂度为线性的嘛。