简单不先于复杂，而是在复杂之后。

目录

1. 汉诺塔问题 

1.1 简介及思路

1.2 代码实现

2. 青蛙跳台阶问题 

2.1 简介及思路 

2.2 代码实现 

---

1. 汉诺塔问题 

1.1 简介及思路

汉诺塔问题是一种经典的递归问题，起源于印度传说中的塔 of Brahma。问题描述如下：

有三个柱子A、B、C，A柱子上有n个盘子，这些盘子大小不一，且从上到下依次变大，现在需要将A柱子上的盘子全部移动到C柱子上，移动的过程中必须满足以下三个条件：

1. 每次只能移动一个盘子；
2. 盘子可以移动到任意柱子上，但是必须保证较大的盘子不能放在较小的盘子上面；
3. 每个盘子移动的过程中都必须放在柱子的顶端。

问题的目标是用最少的步数将所有盘子从A柱子移动到C柱子。

汉诺塔问题可以通过递归的方式解决。

假设有n个盘子需要从A柱子移动到C柱子上，我们可以把这个问题分解成三个子问题：

1. 将n-1个盘子从A柱子移动到B柱子上；
2. 将最大的盘子从A柱子移动到C柱子上；
3. 将n-1个盘子从B柱子移动到C柱子上。

这样，我们可以使用递归算法解决汉诺塔问题。

 

1.2 代码实现

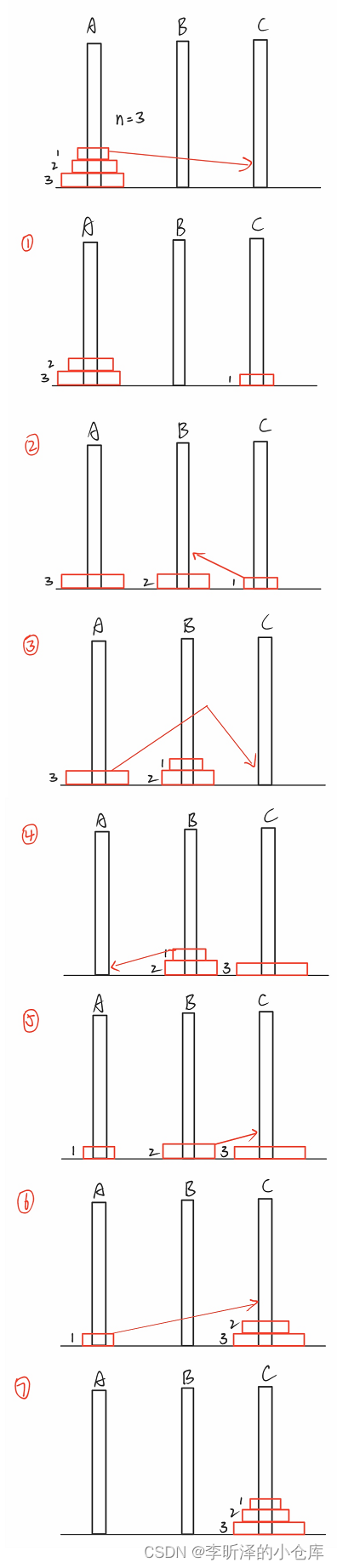
 假如 n 的值为3的话，操作如下：

 

 

 

 

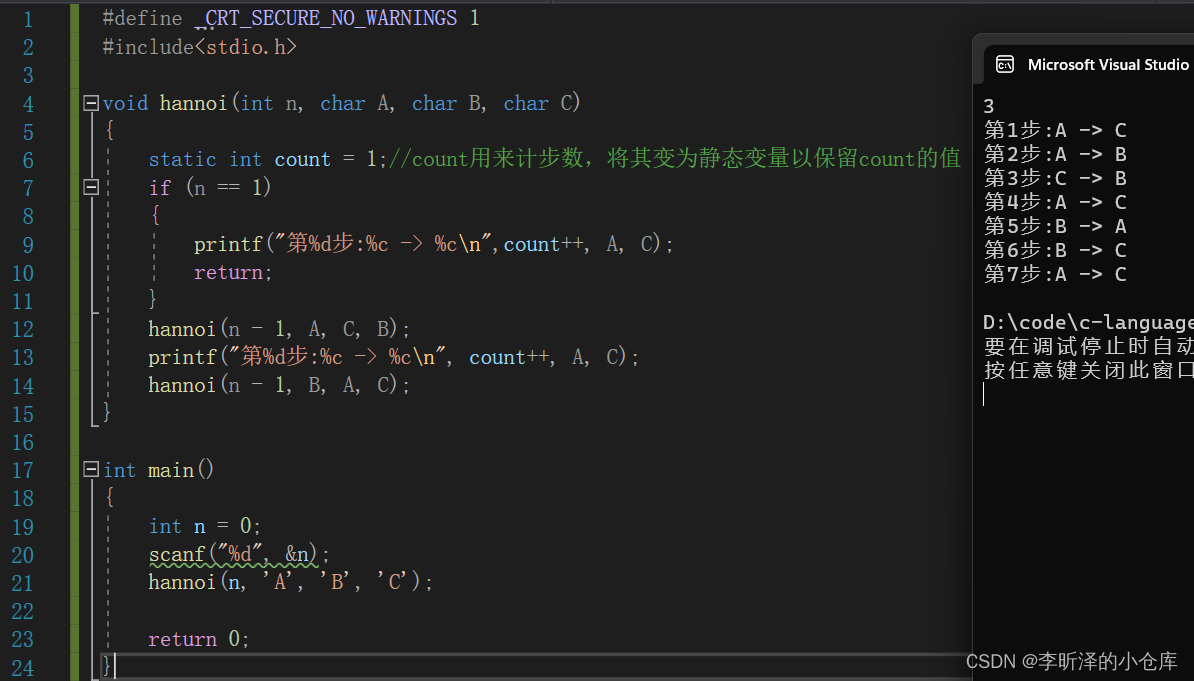
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

void hannoi(int n, char A, char B, char C)
{
	static int count = 1;//count用来计步数，将其变为静态变量以保留count的值
	if (n == 1)
	{
		printf("第%d步:%c -> %c\n",count++, A, C);
		return;
	}
	hannoi(n - 1, A, C, B);
	printf("第%d步:%c -> %c\n", count++, A, C);
	hannoi(n - 1, B, A, C);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	hannoi(n, 'A', 'B', 'C');

	return 0;
}

用归纳法的思想来思考，先考虑盘子只有三个的情况，首先要把A的最上面的盘子移到C，所以在满足限制条件时第一次操作就应该是把A的最上面的盘子移到C，写成 if 语句，括号中的限制条件就是 n == 1 的情况，因为递归的核心就是大事化小，n个盘子的问题可以化解成n-1个盘子加上一个盘子的问题。

倒着思考的话，满足限制条件进行第一步操作时一定是已经‘递’完的情况了，要开始‘归’了，那么应该返回上一级函数，所以在 if 语句中应当加一个 return； 

既然是递归就一定要自己调用自己，所以在 if 语句后面写一个 hanoi 函数，第一个参数是

n-1， 递归中所执行的操作要尽量统一，所以这个函数后面的 printf 语句和 if 中的保持一致。

但是我们现在假设三个盘子的情况，应该把A上的盘子放到B上了，printf 语句中还是

A -> C，所以把参数B和C互换一下就好了。

在第三步要让C -> B，还需要调用一次函数，在这一层B和C已经互换了，所以传参顺序应为‘B’‘A’‘C’。

将程序运行，输入3，和以上画图推理的吻合，也可以用其他的值来测试，程序正确。

2. 青蛙跳台阶问题 

2.1 简介及思路 

这个游戏是这样的：

一只青蛙，一次可以跳一或两个台阶，求青蛙跳 n 个台阶有多少种跳法。 

对于青蛙跳上第 n 个台阶，有两种情况：

1. 青蛙从第 n-1 个台阶跳上来；
2. 青蛙从第 n-2 个台阶跳上来。

因为青蛙每次可以跳一步或两步，所以到达第 n-1 个台阶只有一种跳法，到达第 n-2 个台阶也只有一种跳法。

设跳上第 n 个台阶的跳法数为 f(n)，则有：

f(n) = f(n-1) + f(n-2)

这是一个典型的斐波那契数列，可以使用递归来实现。

2.2 代码实现 

 

 

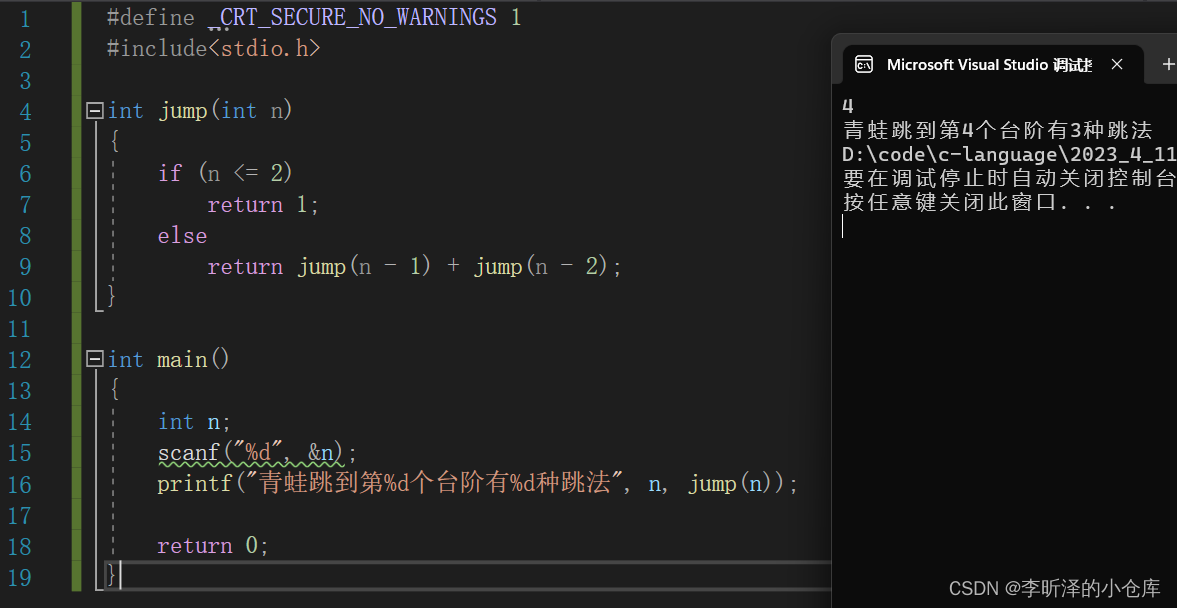
下附代码，可供大家自行测试。

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

int jump(int n)
{
	if (n <= 2)
		return 1;
	else
		return jump(n - 1) + jump(n - 2);
}

int main()
{
	int n;
	scanf("%d", &n);
	printf("青蛙跳到第%d个台阶有%d种跳法", n, jump(n));

	return 0;
}