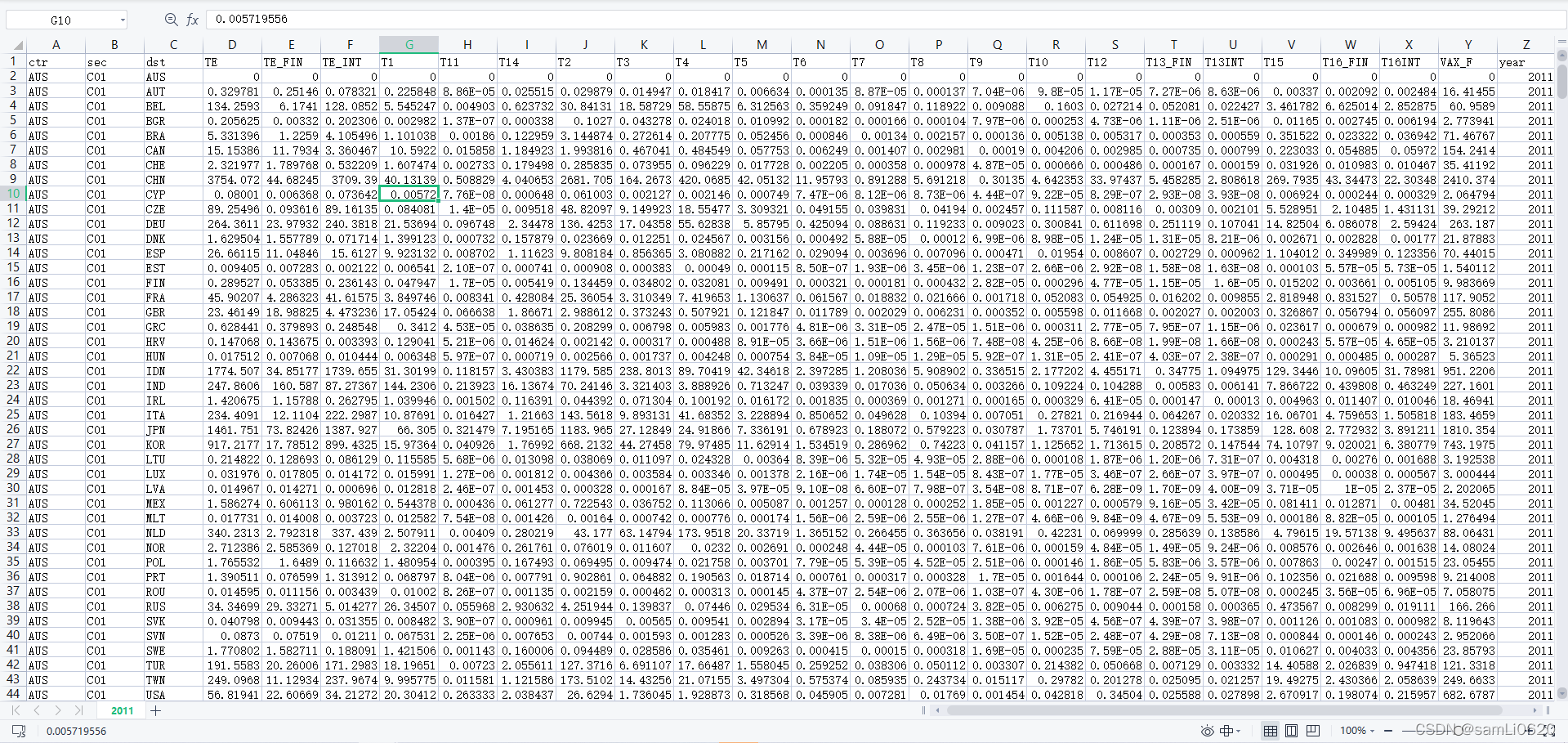
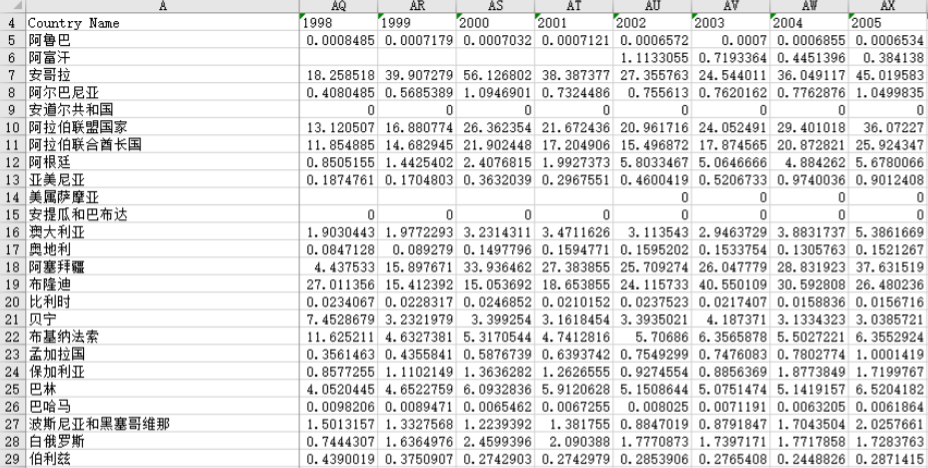
机器学习中的数学基础(三):随机变量
- 3 随机变量
- 3.1 离散型随机变量
- 3.2 连续型随机变量
- 3.3 简单随机抽样
- 3.4 似然函数
- 3.5 极大似然估计
在看西瓜书的时候有些地方的数学推导(尤其是概率论的似然、各种分布)让我很懵逼,本科的忘光了,感觉有点懂又不太懂,基于此,干脆花一点时间简单从头归纳一下机器学习中的数学基础,也就是高数、线代、概率论(其实大学都学过)。
本文全部都是基于我自己的数学基础、尽量用方便理解的文字写的,记录的内容都是我本人记忆不太牢靠、需要时常来翻笔记复习的知识,已经完全掌握的比如极限连续性啥的都不会出现在这里。
学习内容来自这里
3 随机变量
3.1 离散型随机变量
概率函数(概率质量函数) →专为离散型随机变量定义的: p ( x ) = P r o b ( X = x ) , p(x)=Prob(X=x), p(x)=Prob(X=x), X X X是随机变量的取值, P P P是概率。
离散型随机变量概率分布:
f
(
x
)
f(x)
f(x),
f
(
x
i
)
≥
0
,
i
=
1
,
2
,
.
.
.
f(x_i)\geq 0, i=1,2,...
f(xi)≥0,i=1,2,...,
∑
f
(
x
i
)
=
1
\sum f(x_i)=1
∑f(xi)=1。
f
(
x
i
)
=
P
(
X
=
x
)
f(x_i)=P(X=x)
f(xi)=P(X=x)就是离散型随机变量的概率函数。
3.2 连续型随机变量
连续型随机变量画不出离散型随机变量中的分布表。
概率密度→专门描述连续型随机变量的:对于连续型随机变量X,我们不能给出其取每一个值的概率,也就是画不出那个分布表。
即,假如体重范围在50~120kg,那么有没有可能一个人的体重在60.618kg呢?完全有可能,但是在连续型随机变量中,取个别点的概率为0,因为没办法计算一个点!
所以可以用区间来解决,用区间中的频数来计算这个区间的概率,绘制频率分布直方图:
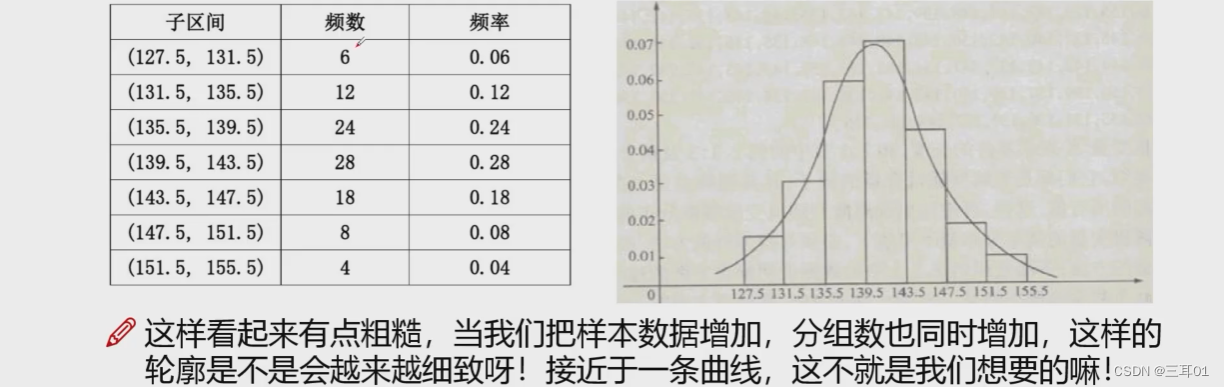
分组越多,轮廓层次感越强,越接近一条曲线;如果组足够多,每个组里只有一个样本,那这个曲线就是描述数据的。
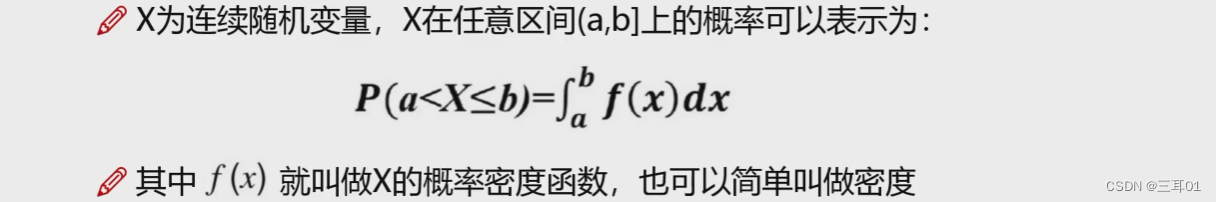
其实求密度就是求每一个区间占的面积,也就是积分。
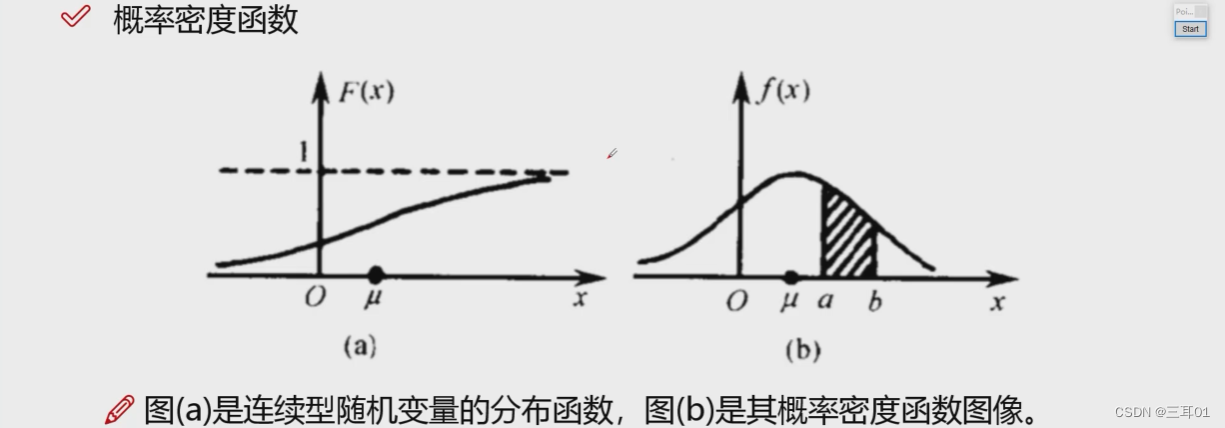
分布函数肯定是越来越接近1的。
3.3 简单随机抽样
抽取的样本满足两点:
(1)样本X1,X2…Xn是相互独立的随机变量;
(2)样本X1,X2.….Xn与总体X同分布。
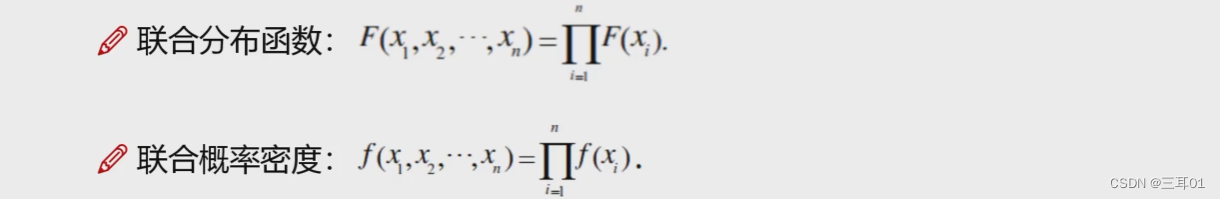
独立同分布,所以联合的可以直接累乘。
3.4 似然函数
似然:拿到了一些样本,但是不知道这些样本是受什么样的参数控制的。
举例:是否下雨有据可循,受到某种参数的影响,这就是
θ
\theta
θ,而x就是一天天的数据。
所以似然函数的目标是把这个
θ
\theta
θ整出来。
离散情况下:


也就是,拿到了一个结果以后,是什么参数使这个结果的可能性更大。
连续情况下:

对于离散和连续(后面的常数可以约掉),最后的结果都是一样的。
总结:
概率:给定参数
θ
\theta
θ时,X=x的可能性;
似然:给定样本X=x时,参数
θ
\theta
θ的可能性!
3.5 极大似然估计
理解:

找到一个参数,使得在这个参数值下,样本出现的概率最大。
怎么解?
- 先构造似然函数:

- 对似然函数取对数,方便求解: ln L ( θ ) \text{ln} L(\theta) lnL(θ)
- 求偏导得到 θ \theta θ值: d ln L d θ = 0 , \frac{d\text{ln}L}{d\theta}=0, dθdlnL=0,虽然前面对似然函数取了对数,这会影响L的极大值,但是对数是单调递增的,并不会影响极值点。
举例: