11.20 至 11.27 五道典型题记录：贪心 | 应用题 | 脑筋急转弯 | 区间问题 | 双指针

松懈了最近，要时刻保持警醒啊！学习不能停，说那么多的借口不如花一些心思去学一些知识，之所以学到的内容不成体系，一方面就是学得少，没多少墨水，怎么也无法高度概括地找到一些骨架性的内容，另一方面需要坚持去学习，长时间全神贯注地做一件事情，并把它做好！我始终相信善始善终和勤能致富，所以要放下一些自己的没用的执着，这篇过后所有的算法题都会加入 C++ 的语言编程，另外有关机器学习的内容现在有时间梳理了，可以找时间认真地学习了，总之，别让自己娱乐至死，让自己的脑袋思考起来，记起来，不管是代码 | 程序 | 知识点 | 歌词 | 乐曲，要让自己时刻保持向上的学习精神，有关MATLAB的内容，进行一个完善梳理，把手头学到的内容好好整理一下，以备不时之需，关于自己的代码编程也写一个工作手册，存放起来。往前走，迈步走，默默向上游~
部分代码借鉴他人，提前说一声，这并不都是我自己码出来的。~~

808. 分汤（贪心 | dfs | 应用题）

题目链接：808. 分汤
题目大意：有 A 和 B 两种类型的汤。一开始每种类型的汤有 n 毫升。有四种分配操作：
提供 100ml 的汤A 和 0ml 的汤B 。 | 提供 75ml 的汤A 和 25ml 的汤B 。
提供 50ml 的汤A 和 50ml 的汤B 。 | 提供 25ml 的汤A 和 75ml 的汤B 。
当我们把汤分配给某人之后，汤就没有了。每个回合，我们将从四种概率同为 0.25 的操作中进行分配选择。
如果汤的剩余量不足以完成某次操作，我们将尽可能分配。当两种类型的汤都分配完时，停止操作。
注意不存在先分配 100 ml 汤B 的操作。
需要返回的值：汤A 先分配完的概率 + 汤A和汤B 同时分配完的概率 / 2。返回值在正确答案 10-5 的范围内将被认为是正确的。

例如：

输入: n = 50
输出: 0.62500
解释:如果我们选择前两个操作，A 首先将变为空。
对于第三个操作，A 和 B 会同时变为空。
对于第四个操作，B 首先将变为空。
所以 A 变为空的总概率加上 A 和 B 同时变为空的概率的一半是 0.25 *(1 + 1 + 0.5 + 0)= 0.625。

输入: n = 100
输出: 0.71875

解题思路：非常可怕的一道题，仅读题都让人十分头疼，看评论说这是一道非常经典的概率问题，用例的上限大致为4800，读题可以发现四种情况全是围绕25的倍数进行分配，所以这是一个简化运算的出发点，使用深度递归进行处理，注意需要配合 @cache 优化运算。
时间复杂度： $ O(C^2)$ ，其中 C约为200。
空间复杂度： $O(C^2)$

class Solution:
    def soupServings(self, n: int) -> float:
        @cache
        def dfs(i,j):
            if i<=0 and j<=0:
                return 0.5
            if i<=0:
                return 1
            if j <=0:
                return 0
            return 0.25*(dfs(i-4,j)+dfs(i-3,j-1)+dfs(i-2,j-2)+dfs(i-1,j-3))
        return 1 if n>4800 else dfs((n+24)//25,(n+24)//25)

808. 香槟塔（贪心 | 找规律）

题目链接：808. 香槟塔
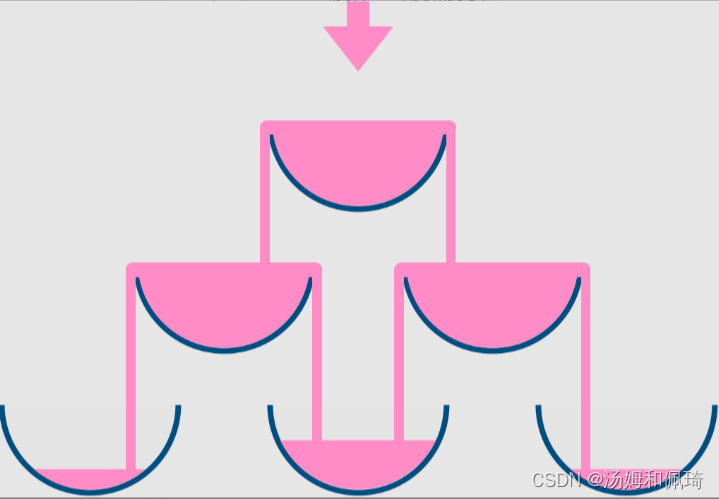
题目大意：把玻璃杯摆成金字塔的形状，其中第一层有 1 个玻璃杯，第二层有 2 个，依次类推到第 100 层，每个玻璃杯 (250ml) 将盛有香槟。

从顶层的第一个玻璃杯开始倾倒一些香槟，当顶层的杯子满了，任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了，就会等流量的流向它们左右两边的杯子，依次类推。（当最底层的玻璃杯满了，香槟会流到地板上）

例如，在倾倒一杯香槟后，最顶层的玻璃杯满了。倾倒了两杯香槟后，第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后，第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后，第三层中间的玻璃杯盛放了一半的香槟，他两边的玻璃杯各自盛放了四分之一的香槟，如下图所示。

例如：
在这里插入图片描述

输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.00000
解释: 我们在顶层（下标是（0，0））倒了一杯香槟后，没有溢出，因此所有在顶层以下的玻璃杯都是空的。

输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1
输出: 0.50000
解释: 我们在顶层（下标是（0，0）倒了两杯香槟后，有一杯量的香槟将从顶层溢出，位于（1，0）的玻璃杯和（1，1）的玻璃杯平分了这一杯香槟，所以每个玻璃杯有一半的香槟。

输入: poured = 100000009, query_row = 33, query_glass = 17
输出: 1.00000

解题思路：逐行循环遍历，一定要读懂题目啊！
时间复杂度： $O(N^2)$ ，N为query_row
空间复杂度： $O (N)$

class Solution:
    def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:
        row = [poured]
        for i in range(1,query_row+1):
            nextRow = [0] * (i+1)
            for j,v in enumerate(row):
                if v>1:
                    nextRow[j] += (v-1)/2
                    nextRow[j+1] += (v-1)/2
            row = nextRow
        return min(1,row[query_glass])

795. 区间子数组个数（区间阻断非常巧妙的子函数编写）

题目链接：795. 区间子数组个数
题目大意：给你一个整数数组 nums 和两个整数：left 及 right 。找出 nums 中连续、非空且其中最大元素在范围 [left, right] 内的子数组，并返回满足条件的子数组的个数。

生成的测试用例保证结果符合 32-bit 整数范围。

例如：

输入：nums = [2,1,4,3], left = 2, right = 3
输出：3
解释：满足条件的三个子数组：[2], [2, 1], [3]

输入：nums = [2,9,2,5,6], left = 2, right = 8
输出：7

解题思路：学习子函数的编写非常地巧妙，由于查询的子区间连续，所以：
符合要求的子区间个数 = 小于right的子区间个数 - 小于left-1的子区间个数
时间复杂度： $O (N)$ ，N为数组nums的长度
空间复杂度： $O (1)$

class Solution:
    def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:
        def f(x):
            cnt=t=0
            for v in nums:
                t=0 if v>x else t+1
                cnt += t
            return cnt
        return f(right)-f(left-1)

809. 情感丰富的文字（计数 | 双指针）

题目链接：809. 情感丰富的文字
题目大意：有时候人们会用重复写一些字母来表示额外的感受，比如 “hello” -> “heeellooo”, “hi” -> “hiii”。我们将相邻字母都相同的一串字符定义为相同字母组，例如：“h”, “eee”, “ll”, “ooo”。

对于一个给定的字符串 S ，如果另一个单词能够通过将一些字母组扩张从而使其和 S 相同，我们将这个单词定义为可扩张的（stretchy）。扩张操作定义如下：选择一个字母组（包含字母 c ），然后往其中添加相同的字母 c 使其长度达到 3 或以上。

例如，以 “hello” 为例，我们可以对字母组 “o” 扩张得到 “hellooo”，但是无法以同样的方法得到 “helloo” 因为字母组 “oo” 长度小于 3。此外，我们可以进行另一种扩张 “ll” -> “lllll” 以获得 “helllllooo”。如果 s = “helllllooo”，那么查询词 “hello” 是可扩张的，因为可以对它执行这两种扩张操作使得 query = “hello” -> “hellooo” -> “helllllooo” = s。

输入一组查询单词，输出其中可扩张的单词数量。

例如：

输入： 
s = "heeellooo"
words = ["hello", "hi", "helo"]
输出：1
解释：
我们能通过扩张 "hello" 的 "e" 和 "o" 来得到 "heeellooo"。
我们不能通过扩张 "helo" 来得到 "heeellooo" 因为 "ll" 的长度小于 3 。

解题思路：本来一直想用 Counter 计数器来做这道题，搞老半天，不行，这道题的字符串是有序的，而Counter专注于计数，所以还是需要用双指针来做比较合理！
时间复杂度： $\sum_i |\textit{words}_i|)$ ， $\textit{words}_i$ 为words第 i 个元素的长度，n 为words的长度，m为字符串s的长度。
空间复杂度： $O (1)$

class Solution:
    def expressiveWords(self, s: str, words: List[str]) -> int:
        
        def check(word):
            i = j = 0
            while i<len(word) and j<len(s):
                if word[i] != s[j]:
                    return False
                ch = word[i]
                c1 = c2 = 0
                while i<len(word) and word[i]==ch:
                    c1 += 1
                    i += 1
                while j<len(s) and s[j]==ch:
                    c2 += 1
                    j += 1
                if c1 > c2 or (c1 != c2 and c2 < 3):
                    return False
            return i==len(word) and j==len(s)

        return sum(int(check(word)) for word in words)

1752. 检查数组是否经排序和轮转得到（非递减 | 脑筋急转）

题目链接：1752. 检查数组是否经排序和轮转得到
题目大意：给你一个数组 nums 。nums 的源数组中，所有元素与 nums 相同，但按非递减顺序排列。

如果 nums 能够由源数组轮转若干位置（包括 0 个位置）得到，则返回 true ；否则，返回 false 。

源数组中可能存在重复项。

注意：我们称数组 A 在轮转 x 个位置后得到长度相同的数组 B ，当它们满足 A[i] == B[(i+x) % A.length] ，其中 % 为取余运算。

例如：

输入：nums = [3,4,5,1,2]
输出：true
解释：[1,2,3,4,5] 为有序的源数组。
可以轮转 x = 3 个位置，使新数组从值为 3 的元素开始：[3,4,5,1,2] 。

输入：nums = [2,1,3,4]
输出：false
解释：源数组无法经轮转得到 nums 。

输入：nums = [1,2,3]
输出：true
解释：[1,2,3] 为有序的源数组。
可以轮转 x = 0 个位置（即不轮转）得到 nums 。

解题思路：别想复杂了，简单考虑非递减的子区间大于1即返回False，还有注意 % 的运用！
时间复杂度： $O (N)$ ，N为数组nums的长度。
空间复杂度： $O (1)$

class Solution:
    def check(self, nums: List[int]) -> bool:
        return sum(nums[i] > nums[(i+1)%len(nums)] for i,v in enumerate(nums)) < 2

总结

努力奋斗！粤语不好学啊，九声六调，韵母还贼多，害，学学吧，没啥好怕的，要保持积极向上的精神，昨天学了一句英文，非常不错，记录一下：
I’m an honest, upright, decent man. ------ 我是一个诚实、秉直、正派的人。