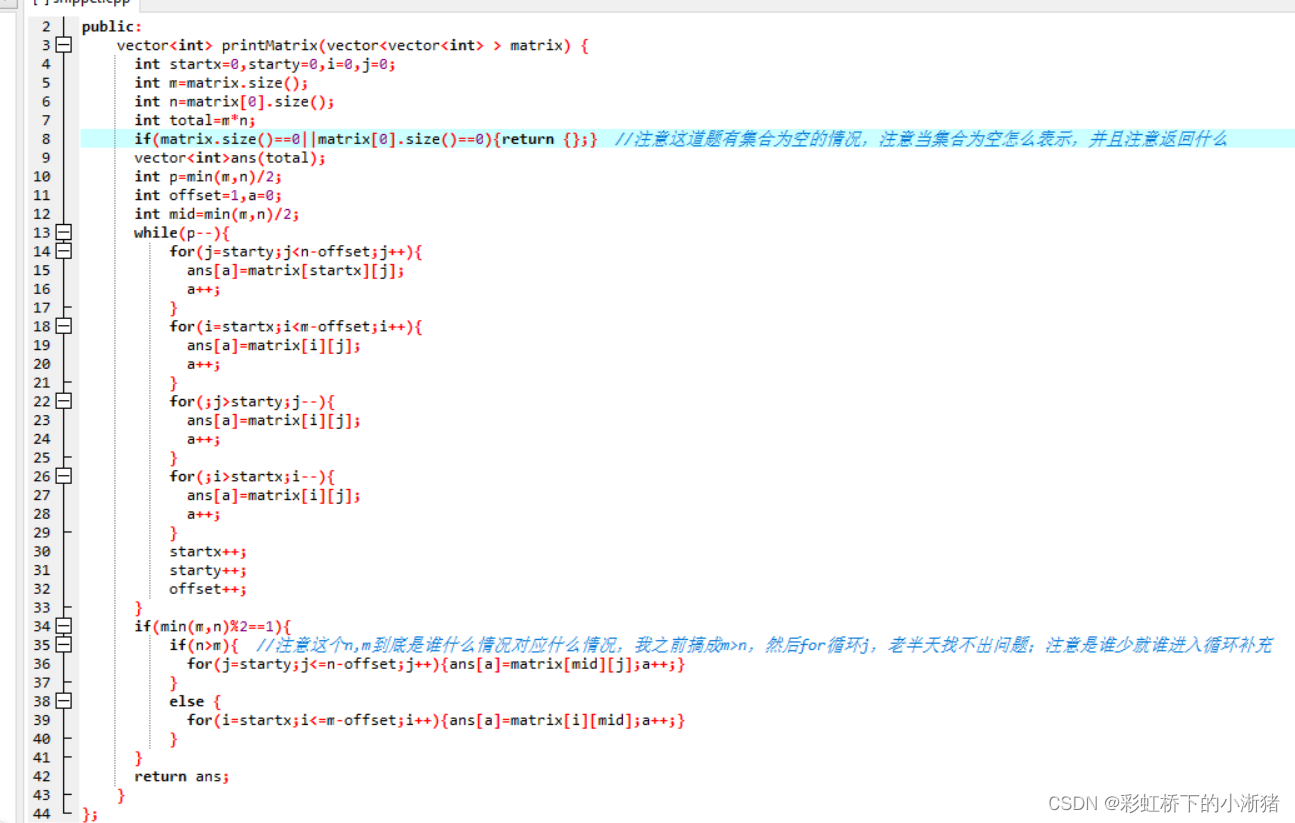
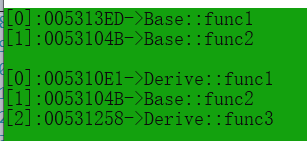
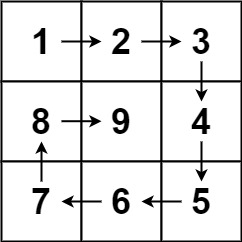
n等于几,螺旋矩阵最外层行列数就等于几。如n等于3所以最外层一圈的行、列都是3个数字,如左图,n等于4所以最外层的行、列都是4个数字,如右图:
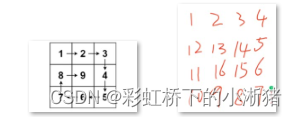
题目要求我们输出(以n=3为例)[[123][894][765]],题目只是给我们一堆数字,我们怎样才能输出题目要输出的结果呢?我们要做的是把这些数字按顺时针螺旋式一个位置一个位置填充进去,然后再返回这个二维数组即可(因为二维数组它的保存顺序就是从第一行从左到右然后再第二行从左到右如此下去的,所以返回这个二维数组就是返回我们想要的[[123][894][765]]。
接下来就是如何顺时针螺旋式填充这个二维数组啦。
http://【一入循环深似海 | LeetCode:59.螺旋矩阵II-哔哩哔哩】 https://b23.tv/vN31TwF
还记得二分法里一定要坚持的循环不变原则,螺旋矩阵也要坚持循环不变量原则,这个很重要。需要定好矩阵的四个角落怎么分配,我们坚持左闭右开的原则,即下图这样,如第一行左角落包含进去而右角落不包含进去,同理第四列上角落包含进去下角落不包含进去...这样就能保证同一圈的每行每列填充的数量都是一样的,这样代码才不会越写越乱,不然一会左闭右开一会左开右闭一会又左闭右闭,就会越写越乱。
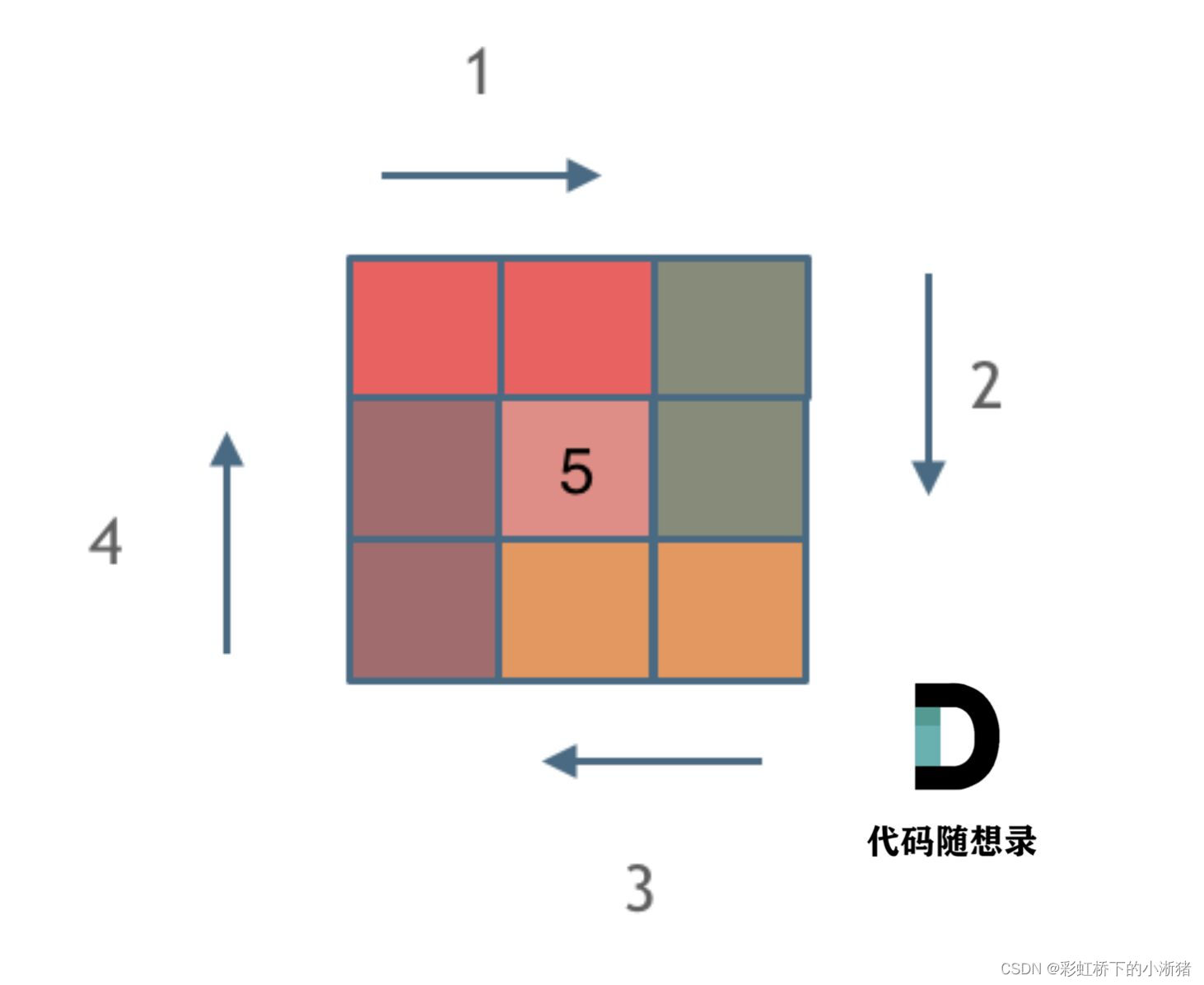
套路大致是这样:(以n=4为例)
vector<vector<int>>sums(n,vector<int>(n,0)); //首先定义一个二维数组
startx=0,starty=0;
//我们坐标是(i,j),i是上下方向,j是左右方向,然后定义初始的位置即startx,starty(0,0)嘛,从第一行第一个位置开始
offset=1,count=1; int i,j;
//offset是为了控制每一圈里每一条边遍历的长度,我们后面会用到n-offset,如第一行我们是只要填充第1,2,3个位置,第4个位置我们是不填充的,所以j<n-offset即j<3,因为我们i,j是从0开始的嘛,所以小于3即只填充0,1,2,这3个位置。count是填充进去的数,即用来给矩阵每一个空格赋值的。
int mid=n/2; //矩阵中间的位置
int loop=n/2; //是循环几圈
while(loop--){ //是循环几圈的,如果n为奇数3即循环1圈即可然后再额外填最中间那个
for ( j=starty ; j<n-offset ; j++){ sums [startx] [j] = count;count++;}
for ( i=startx ; i<n-offset ; i++){ sums [i] [j] =count; count++;}
for ( ; j>starty ; j--){ sums [i] [j] = count; count++;} //因为j就是从j开始所以是空;
for ( ; i>startx ; i--){ sums [i] [j] = count; count++;}
startx++;
starty++;
//如第二圈开始位置就变成(1,1)了,所以每填充完一圈,startx和starty都要++
offset++;
//如第二圈第一行只能填充1个,注意不是4-2=2,所以第二圈每一条边遍历的长度为2,看图就知道第二圈如上行只能填充13,14是留给右行的。那j<n-offset=4-2,不就是0,1两个嘛?因为这时候第二圈j是从1开始了,所以是只有1即一个长度。
}
if (n%2=1){sums[mid][mid]=count;}
//如果n为奇数,就还需要给矩阵最中间的位置赋值
return sums;
//注意要理解当中间有一个时比如最中间那个5,为什么要在循环外加入sums数组中,而不是在循环里就加上。因为例如n=3,到了第二圈n-offset=3-2=1,而我们有要控制的遍历长度规则就是j要<n-offset=1的且此时j已经为1,1不<1,所以进入不了循环,所以需要在循环外把它额外加入数组sums中。
同类型题
①leetcode 59.螺旋矩阵II (就是以这道题为例的)
②leetcode 54.螺旋矩阵
③剑指offer 29.顺时针打印矩阵
②③是同一种题,注意此时和59题又有点不一样了。
有哪些不同?最好自己画几个图看看更直观。
第一个不同:循环完圈后长方形的矩形有剩下一行或者一列的情况
59题因为题目给出的是以一个数的平方为矩阵,所以这个矩阵一定是正方形,正方形是不会出现循环圈后中间还剩下一行或者一列的情况,而54,29题有可能是正方形也有可能是长方形,而长方形就有可能出现循环完圈后中间还剩下一行或一列的情况,所以需要注意好循环后补充中间剩下的一行或一列的情况。
第二个不同:循环几圈的判断不同
59题如上面说的,循环n/2圈即可。而54,29不一样,是根据行数和列数其中最小的那个来判断,用最小的那个/2,这才是要循环的圈数。你画几个例子图看看就知道了
相同点:
第一,还是遵循循环不变量原则,即每一圈每一条边需要遍历的长度要按照左闭右开的原则,只不过因为59是正方形所以i,j都<n-offset即可;而54,29不一样,有可能是长方形了,就有可能上行需要遍历3个而右行只需遍历2个,所以要根据具体的行数列数具体分析,但是思路是一样的,左闭右开即都把最后一个角落的数给下一个循环遍历,所以是j<m-offset,i<n-offset。
第二,还是循环绕圈的思想通过循环把数获取出来,中间剩下的再在循环外添加,只不过现在多了可能剩下的是一行数或者一列数而已。
还有一些要注意的:
怎么判断中间剩下的是一个数还是一行数还是一列数?
当行数和列数其中最小的那个为奇数时,就有剩下的是一行或一列的情况。然后如果行数<列数时剩下的就是一行数,如果行数>列数剩下的就是一列数,注意是谁少就留下谁的,如果相等,则剩下的就是一个数。
然后如果有剩下的一个数一行数或者一列数的情况,就在循环外把它加进数组,因为是一行或一列所以是用for循环把它放进ans数组里。
补充一点知识:对于二维数组ass[][],怎么判断它的行数和列数,我是个笨蛋老是搞乱。
ass.size() 指的就是多少行,上下方向的行数
ass[0].size() 指的就是多少列,左右方向的列数
leetcode 54:
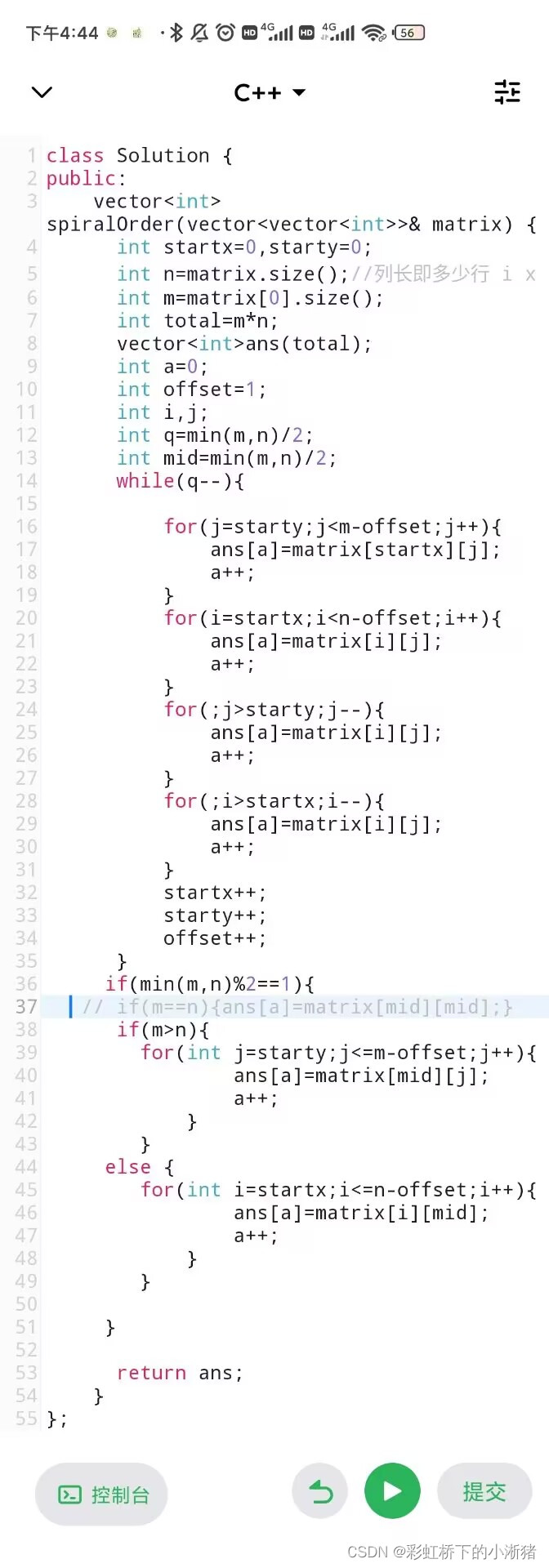
剑指offer29: