小朋友们好，大朋友们好！

我是猫妹，一名爱上Python编程的小学生。

欢迎和猫妹一起，趣味学Python。

今日主题

最近猫妹一直在练习Python编程，有些习题真是经典啊！

比如韩信点兵问题，比如鸡兔同笼问题等。

这些问题，第一次遇到，真是没有思路，懂了之后，真是有趣啊！

这里猫妹简单记录下，便于以后回看。

什么是举一反三呢？

学习掌握一个类型的题目后，类似问题也都迎刃而解、不在话下。

韩信点兵问题

小朋友，你听过韩信吗？

韩信，汉初三杰，汉初著名的军事家，被后人奉为“兵仙”、“神帅”。

我们现在常用的很多成语，很多都和韩信有关系。

比如胯下之辱、一饭千金、国士无双、明修栈道暗渡陈仓

比如背水一战、独当一面、十面埋伏、成也萧何败也萧何

比如功高震主、推陈出新、金石之交、置之死地而后生

我们今天不聊历史，我们今天也不聊语文，我们今天聊聊韩信点兵问题。

题目是这样的：

一次，韩信大将军派出1000士兵打仗，韩信用用兵如神，把敌人全部歼灭，得胜回营，清点所剩士兵。

据初步估计战死的士兵在200—300之间，韩信命令士兵排队，3人一排，剩2人；5人一排剩3人；7人一排剩2人，韩信就知道具体士兵人数。

我们理解下题目，韩信派出1000士兵打仗，预估阵亡200~300之间，也就是会所有700~800士兵还活着，具体有多少呢？

假设还有活着的士兵人数为x，那么x除以3,余数为2，x除以5,余数为3，x除以7,余数为2。

我们要知道，计算机计算速度是非常快的，像这样问题，直接让计算机从700~800逐一检查就可以了，几秒之内搞定。

前提是，你把正确的指令告诉计算机。

第3行语句为控制逻辑，从700~800，逐一检查。

第4行语句为判断逻辑，3人一排余2人；5人一排余3人；7人一排余2人的程序表达。

第5行语句，当满足条件时，将结果打印出来。

鸡兔同笼问题

大约在1500年前，《孙子算经》中就记载了这个有趣的问题：

“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”

我们按照韩信点兵的思路，外面循环里面判断，符合结果打印出来。

今有物不知几何

《孙子算经》中还记载了这样一个问题：

“今有物不知其数，三三数之剩二；五五数之剩三，七七数之剩二；问物几何？”

假如100之内，哪些数符合上述条件呢？

闰年计算

小朋友，你知道什么是闰年吗？

1582年以来公历的置闰规则：

普通闰年：公历年份是4的倍数，且不是100的倍数的，为闰年（如2004年、2020年等就是闰年）。

世纪闰年：公历年份是整百数的，必须是400的倍数才是闰年（如1900年不是闰年，2000年是闰年）。

你能输出2000年到2500年之间的所有闰年年份吗？

我们理解下，可以被400整除的是闰年(世纪闰年)，另外可以被4整除但不可以被100整除的也是闰年(普通闰年)。

三角形

我们生活中有很多三角形，你身边有三角形物体吗？

三角形有三个边，有三个角。

三条边必须满足，任意两条边大于第三条边。

题目来了：任意输入三个整数，请判断，这三条边是否可以构成三角形。

勾股定理

三角形中，如果有一个角为直角，那么这个三角形为直角三角形。

勾股定理：在任何一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方。

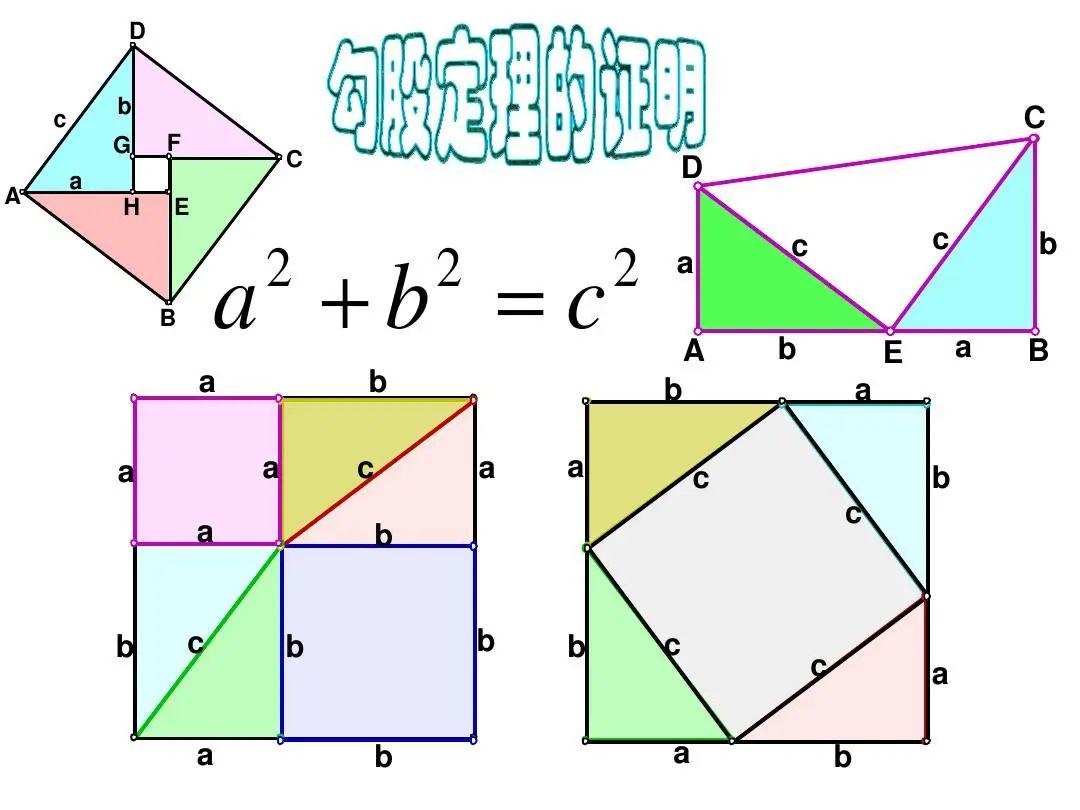
题目来了，任意输入三个整数，请判断，这三条边是否可以构成直角三角形。

我们把上述三角形题目结合起来，任意输入三条边，请判断是否可以构成三角形，如果可以构成三角形，请判断是否可以构成直角三角形。

最后再抛出个问题，100之内的数字，都有哪些数字可以构成直角三角形？

如果遇到什么问题，咱们多多交流，共同解决。

我是猫妹，咱们下次见！