目录
题目一:力扣547题,求省份数量
题目二:岛屿数量
题目三:岛屿数量拓展
什么是并查集,举个简单的例子。学生考试通常会以60分为及格分数,我们将60分及以上的人归类为及格学生,而60分以下归类为不及格的学生, 通过记录学生ID。现在要求根据学生的ID,迅速的找出这名学生成绩是否及格。这种归类就是合并,而根据学生ID查找就是查询,合起来就是并查集。
可能会有人说不用并查集也可以干这件事情,但是有没有想过一个问题,一个班级,一个年级,一个市,一个省,全中国。如果都要统计这些信息呢?如果要统计及格的全部人数呢?难到要一个一个去查吗?此处,并查集就发挥作用了。
下面推荐一篇博客,对并查集的解释还算通俗易懂,有兴趣的朋友可以看看https://blog.csdn.net/LWR_Shadow/article/details/124873281
下面来分享一些并查集的算法题:
题目一:力扣547题,求省份数量
题目的具体信息可以直接查看547. 省份数量
这是一道奇葩的题目,非此即彼,只要不相连的城市,就属于其他省。而现实中,比如苏州和无锡相连接,徐州和他们都不相连,但是无锡、苏州、徐州却都属于江苏省。既然题目是这么要求的,那我们就按照要求进行设计。
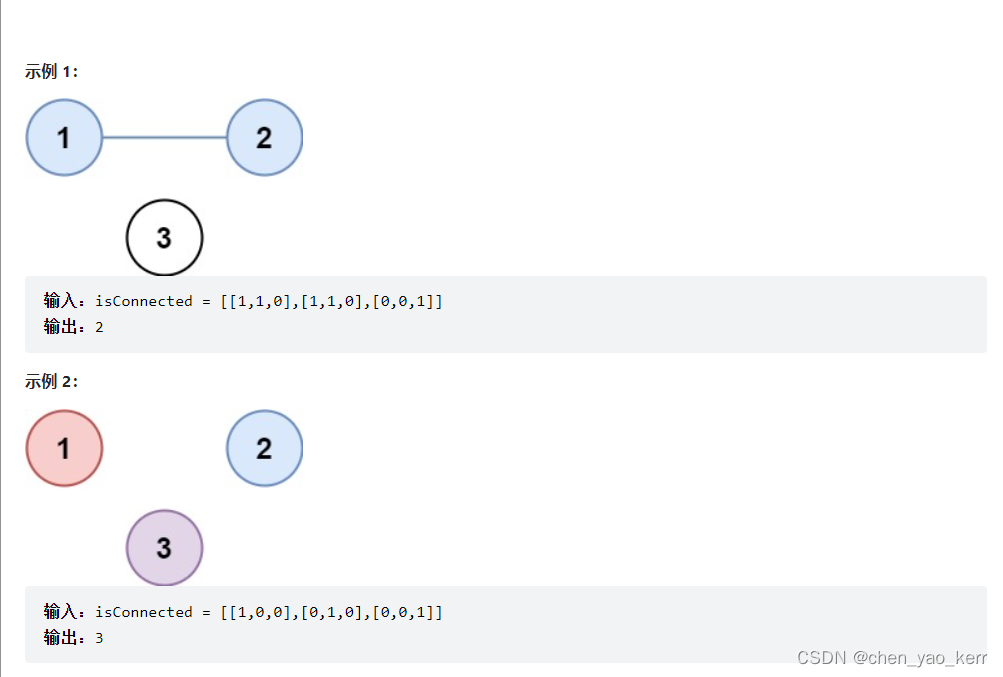
式例1:这组二维数组是什么意思呢?
从1节点的角度:【1,1,0】代表1节点自己连接自己,自己连接2节点,不连接点3节点。
从2节点的角度:【1,1,0】自己连接1节点,自己连接自己,自己不连接3节点。
从3节点的角度:【0,0,1】自己不连接1节点,不连接2节点,自己连接自己。
所以,得出的结论是节点1和节点2是同一个省,而3节点是另外一个省的城市,共2个省份
式例2:完全按照上方分析的思路去分析,节点1、节点2、节点3互不连接,也就是说他们分别属于不同的省份,这个demo共有3个省份。
下面使用并查集的知识进行解答:
package code03.并查集_04;
/**
*
* 链接 https://leetcode.cn/problems/number-of-provinces/
*/
public class Code01_ProvinceCount {
public static int findCircleNum(int[][] M)
{
int length = M.length;
UnionFind uom = new UnionFind(length);
for (int i = 0; i < M.length; i++) {
for (int j = i + 1; j < length; j++) {
if (M[i][j] == 1) {
uom.union(i, j);
}
}
}
return uom.size();
}
static class UnionFind {
//父节点
private int[] parent;
// 辅助结构
private int[] help;
// 一共有多少个集合
private int sets;
// i所在的集合大小是多少
private int[] size;
UnionFind(int length)
{
parent = new int[length];
size = new int[length];
//help的初始化, 个人想每次调用的时候初始化,但是数据量较大的
//时候可能会吃内存
help = new int[length];
//本题比较特殊,二维数组长度为多少,集合最多就可能是多少
sets = length;
//记录数组的下标地址,可以通过下标找到父亲节点
for (int i = 0; i < length; i++) {
parent[i] = i;
//i所在的集合大小是多少, 默认是自己, 所以是1
size[i] = 1;
}
}
public void union(int i, int j)
{
//获取到的根节点索引. 需要注意的是,第一次调用这i和j,返回的是
//他们本身的索引值。不会涉及到里面的while和for。 这样,我们本
//方法体才能安稳的做合并操作,才会存在下挂的后代节点。
int indexI = findRoot(i);
int indexJ = findRoot(j);
//如果他们两个值不相等,说明他们2个
//还没有成为同一类数据。因此,我们需要
//把他们设置成同一类数据
if (indexI != indexJ)
{
if (size[indexI] >= size[indexJ]) {
/**
* 此处的合并是合并2个不同的节点,将较小的节点指针指向较大的节点,
* 这样就实现了并查集合并的目的.这是功能性合并
*
* 而在findRoot方法中,合并的是同一节点的父节点,起到的是一个性能优化的作用
*/
//等价于parent[indexJ] = parent[indexI], 因为没有合并之前,indexI == parent[indexI]
parent[indexJ] = indexI;
//更新合并后的根节点的后代数量
size[indexI] = size[indexI] + size[indexJ];
//被合并后的根节点,不再保存后代信息
size[indexJ] = 0;
}
else {
parent[indexI] = indexJ;
size[indexJ] = size[indexJ] + size[indexI];
size[indexI] = 0;
}
//因为我们默认的是有几组数据,就有几个省份。 但是此处发生了合并,也就意味着2组数据中
//他们是在相同的省份中,因此默认值需要减少1.
sets--;
}
}
public int size() {
return sets;
}
public int findRoot (int addressIndex)
{
int index = 0;
/**
* 第一次肯定是可以找到地址的,因为每个城市的父节点都是自己,
* 所以他们都是在parent数组中的
*
* 但是, 经过合并后,我们只会保存合并后的父节点的地址下标。
* 数组的形式,我们只是在parent数组中,更新当前城市的父节点
* 下标地址。因此,以下的while循环就出出现了
*/
while (addressIndex != parent[addressIndex]) {
//记录下每一次遍历的父节点的下标,有可能有很多
help[index] = parent[addressIndex];
//指针指向父节点的下标,这样我们就可以逐层
//网上找到最顶层的根节点了。
addressIndex = parent[addressIndex];
index++; //index是比实际找的次数多1的
}
/**
* 我们只是在parent数组中,更新当前城市的父节点下标地址
* 这样我就达到了并查集,合并同类数据的功能
*
* index是比实际找的次数多1的, 所以一开始就需要减1
* 这也就不用担心help里面可能存在的脏数据问题了。
*/
for (index--; index >=0; index--) {
/**
* 路径压缩,把之前每一次找到的父节点下标全部指向了根节点,
* 这样以后再找的话就会减少上面的while循环次数了。
* 因为我们判断是否是同一类数据,就是根据根节点的下标进行判断的
*
* 比如,a 和 b的根节点相同,那么我就可以认为a和b是同一类数据
*
* help数组之前记录了parent数组父节点的下标,因此需要根据
* 下标把这些值都给改成根节点的下标,这样这些节点以后就全部
* 指向根节点了
*/
parent[help[index]] = addressIndex;
}
//其实,返回的就是一个父节点的地址下标值
return addressIndex;
}
}
public static void main(String[] args) {
int[][] isConnected = {{1,1,0},{1,1,0},{0,0,1}};
int size = findCircleNum(isConnected);
System.out.println(size); //预期输出2
int[][] isConnected2 = {{1,0,0},{0,1,0},{0,0,1}};
int size2 = findCircleNum(isConnected2);
System.out.println(size2); //预期输出2
}
}
题目二:岛屿数量
原题可以直接查看200. 岛屿数量
这一题和上一题省份数量有相同和不同的部分:
相同部分是1和1相连接,就属于1片岛屿,还是算1个岛,这点和省份计算是一样的。
不同的部分是,省份中0也代表一个城市,只是它和其他城市不相连;而这道题中,0代表的是水,不是岛屿,因此在初始化的时候是有区别的。

并查集方式实现:
package code03.并查集_04;
/**
* https://leetcode.com/problems/number-of-islands/
* 并查集方式实现
*/
public class Code02_NumberOfLands {
public int numIslands(char[][] grid)
{
if (grid == null || grid.length == 0) {
return 0;
}
int rowLength = grid.length;
int colLength = grid[0].length;
UnionFind uf = new UnionFind(grid);
//合并第一行
for (int j = 1; j < colLength; j++) {
if (grid[0][j - 1] == '1' && grid[0][j] == '1') {
uf.union(0, j - 1, 0, j);
}
}
//合并第一列
for (int i = 1; i < rowLength; i++) {
if (grid[i - 1][0] == '1' && grid[i][0] == '1') {
uf.union(i - 1, 0, i, 0);
}
}
//从第二行第二列开始遍历
for (int i = 1; i < rowLength; i++) {
for (int j = 1; j < colLength; j++) {
if (grid[i][j] == '1') {
//上一行合并
if (grid[i][j - 1] == '1') {
uf.union(i, j - 1, i, j);
}
//前一列合并
if (grid[i - 1][j] == '1') {
uf.union(i - 1, j, i, j);
}
}
}
}
return uf.sets;
}
static class UnionFind
{
int[] parents;
int[] size;
int sets;
int[] helps;
int row;
int col;
public UnionFind(char[][] gg)
{
row = gg.length;
col = gg[0].length;
int length = row * col;
parents = new int[length];
size = new int[length];
helps = new int[length];
sets = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
//优化,只有是1的是,才会更新parent下标为自己
if (gg[i][j] == '1') {
//生成唯一地址
int index = index(i, j);
//默认自己就是自己的父亲节点
parents[index] = index;
//每个父节点下挂的节点数量,默认为1
size[index] = 1;
//默认每出现1都是一个岛屿
sets++;
}
}
}
}
public void union (int row1, int col1, int row2, int col2)
{
//父节点
int parentIndex1 = index(row1, col1);
int parentIndex2 = index(row2, col2);
//根节点
int rootIndex1 = findRoot(parentIndex1);
int rootIndex2 = findRoot(parentIndex2);
//根节点不同,则合并
if (rootIndex1 != rootIndex2) {
//将小的挂在大的下面
if (size[rootIndex1] >= size[rootIndex2]) {
parents[rootIndex2] = rootIndex1;
size[rootIndex1] = size[rootIndex1] + size[rootIndex2];
size[rootIndex2] = 0;
}
else {
parents[rootIndex1] = rootIndex2;
size[rootIndex2] = size[rootIndex1] + size[rootIndex2];
size[rootIndex1] = 0;
}
sets--;
}
}
public int index (int r, int c) {
//列的长度是固定的col
return r * col + c;
}
public int findRoot (int index)
{
int rootIndex = 0;
//并查集之前合并过
while (index != parents[index]) {
//记录下每一次找到的上层节点(父节点)
helps[rootIndex] = parents[index];
//当前地址指向上层节点(父节点)
index = parents[index];
rootIndex++;
}
//路径压缩
for (rootIndex--; rootIndex > 0; rootIndex--) {
//返回原始收集的上层节点地址下标
int t = helps[rootIndex];
//根据下标,更新到根节点地址,
//这样所以的地址都指向了根点处,优化了性能
parents[t] = index;
}
return index;
}
}
public static void main(String[] args) {
char[][] bb = {{'1','1','1','1','0'},{'1','1','0','1','0'},{'1','1','0','0','0'},{'0','0','0','0','0'}};
Code02_NumberOfLands tt = new Code02_NumberOfLands();
int num = tt.numIslands(bb);
System.out.println(num);
}
}
渲染方式实现:
package code03.并查集_04;
/**
* 感染方式实现,性能非常高
* 局限是部分案例无法解决
*/
public class Code02_NumberOfLands_extension {
public int numIslands(char[][] grid)
{
if (grid == null || grid.length == 0) {
return 0;
}
int num = 0;
for (int row = 0; row < grid.length; row++) {
for (int col = 0; col < grid[row].length; col++) {
if (grid[row][col] == '1') {
num++;
infect(grid, row, col);
}
}
}
return num;
}
public void infect (char[][] bb, int row, int col)
{
if (row < 0 || row == bb.length
|| col < 0 || col == bb[0].length
|| bb[row][col] != '1') {
return;
}
bb[row][col] = 0;
//上
infect(bb, row-1, col);
//下
infect(bb, row+1, col);
//左
infect(bb, row, col-1);
//右
infect(bb, row, col+1);
}
public static void main(String[] args) {
char[][] bb = {{'1','1','1','1','0'},{'1','1','0','1','0'},{'1','1','0','0','0'},{'0','0','0','0','0'}};
Code02_NumberOfLands_extension tt = new Code02_NumberOfLands_extension();
int num = tt.numIslands(bb);
System.out.println(num);
}
}
这一道题,渲染的方式是最优解,它的性能是高于并查集实现方式的。但是,并查集的方式可以解决很多渲染方式无法解决的问题。 因此,渲染方式和并查集方式,我们都要掌握。
题目三:岛屿数量拓展
这是一道收费题:https://leetcode.com/problems/number-of-islands-ii/
* 题目: * 设定一个二维数组,行为 m 列为 n. * 现在给你一组地标数据,可以定位二维数组的具体位置。 每个地标都代表有1个岛屿, * 但是如果连在一起的话只能算做一个岛。要求每次空降一次数据,求每次的岛屿数量。 * * 假设 3 行 3列的 二维数组。 * 给定的坐标为:[[0,0],[0,1],[1,2],[2,,1]] * 【0,0】位置确定,此时岛为1 * 【0,1】位置确定,此时岛为1 * 【1,2】位置确定,此时岛为2 * 【2,1】位置确认,此时岛为3 * * 输出的结果为: 【1,1,2,3】 * 请设计一种算法
package code03.并查集_04;
import java.util.ArrayList;
import java.util.List;
/**
* https://leetcode.com/problems/number-of-islands-ii/
*
* 题目:
* 设定一个二维数组,行为 m 列为 n.
* 现在给你一组地标数据,可以定位二维数组的具体位置。 每组数据都代表有1个岛屿,
* 但是如果连在一起的话只能算做一个岛。要求每次空降一次数据,求每次的岛屿数量。
*
* 假设 3 行 3列的 二维数组。
* 给定的坐标为:[[0,0],[0,1],[1,2],[2,,1]]
* 【0,0】位置确定,岛为1
* 【0,1】位置确定,岛为1
* 【1,2】位置确定,岛为2
* 【2,1】位置确认,岛为3
*
* 输入的结果为: 【1,1,2,3】
* 请设计一种算法
*/
public class Code03_NunbOfLandsII {
public List<Integer> numIslands(int m, int n, int[][] positions)
{
List<Integer> list = new ArrayList<>();
if (m < 0 || n < 0 ||
positions == null || positions.length == 0
|| positions[0].length == 0) {
return list;
}
//此时的初始化内部不同于之前的初始化
UnionFind uf = new UnionFind(m, n);
for (int[] position : positions) {
list.add(uf.connect(position[0], position[1]));
}
return list;
}
static class UnionFind
{
private int[] parents;
private int[] size;
private int[] helps;
private int sets;
private int col;
private int row;
public UnionFind(int m, int n) {
int length = m * n;
parents = new int[length];
size = new int[length];
helps = new int[length];
sets = 0;
row = m;
col = n;
}
public int connect (int row, int col)
{
//获取当前位置
int curPosition = index(row, col);
//判断空间的位置是否已经是岛屿,默认为0
if (size[curPosition] == 0 ) {
size[curPosition] = 1;
parents[curPosition] = curPosition;
sets++;
//合并,和渲染解题思路有点相似
union(row, col, row-1, col); //上一行
union(row, col, row+1, col); //下一行
union(row, col, row, col-1); //前一列
union(row, col, row, col+1); //后一列
}
return sets;
}
public void union (int row1,int col1, int row2, int col2)
{
//越界,无法合并
if (row1 < 0 || row2 < 0 || col1 < 0 || col2 < 0
|| row1 == row || row2 == row
|| col1 == col || col2 == col) {
return;
}
//父节点
int parentIndex1 = index(row1, col1);
int parentIndex2 = index(row2, col2);
//如果2个中不全是岛屿,则不合并
//需要注意的地方,写忘记了, debug才查出问题
if (size[parentIndex1] == 0 || size[parentIndex2] == 0) {
return;
}
//根节点
int rootIndex1 = findRoot(parentIndex1);
int rootIndex2 = findRoot(parentIndex2);
//根节点不同,则合并
if (rootIndex1 != rootIndex2) {
//将小的挂在大的下面
if (size[rootIndex1] >= size[rootIndex2]) {
parents[rootIndex2] = rootIndex1;
size[rootIndex1] = size[rootIndex1] + size[rootIndex2];
}
else {
parents[rootIndex1] = rootIndex2;
size[rootIndex2] = size[rootIndex1] + size[rootIndex2];
}
sets--;
}
}
public int index (int r, int c) {
return r * col + c;
}
public int findRoot (int index)
{
int rootIndex = 0;
//并查集之前合并过
while (index != parents[index]) {
//记录下每一次找到的上层节点(父节点)
helps[rootIndex] = parents[index];
//当前地址指向上层节点(父节点)
index = parents[index];
rootIndex++;
}
//路径压缩
for (rootIndex--; rootIndex > 0; rootIndex--) {
//返回原始收集的上层节点地址下标
int t = helps[rootIndex];
//根据下标,更新到根节点地址,
//这样所以的地址都指向了根点处,优化了性能
parents[t] = index;
}
return index;
}
}
public static void main(String[] args) {
int m = 3;
int n = 3;
int[][] positions = {{0,0},{0,1},{1,2},{2,1}};
Code03_NunbOfLandsII tt = new Code03_NunbOfLandsII();
List list = tt.numIslands(3, 3, positions);
for(int i = 0; i < list.size(); i++) {
System.out.println("第 " + (i+1) + " 次空降,岛屿数量为: " + list.get(i));
}
}
}