这是本人的解答,并非官方解答
验证旋转矩阵是正交矩阵
在第44页中,旋转矩阵的引入是这样的:
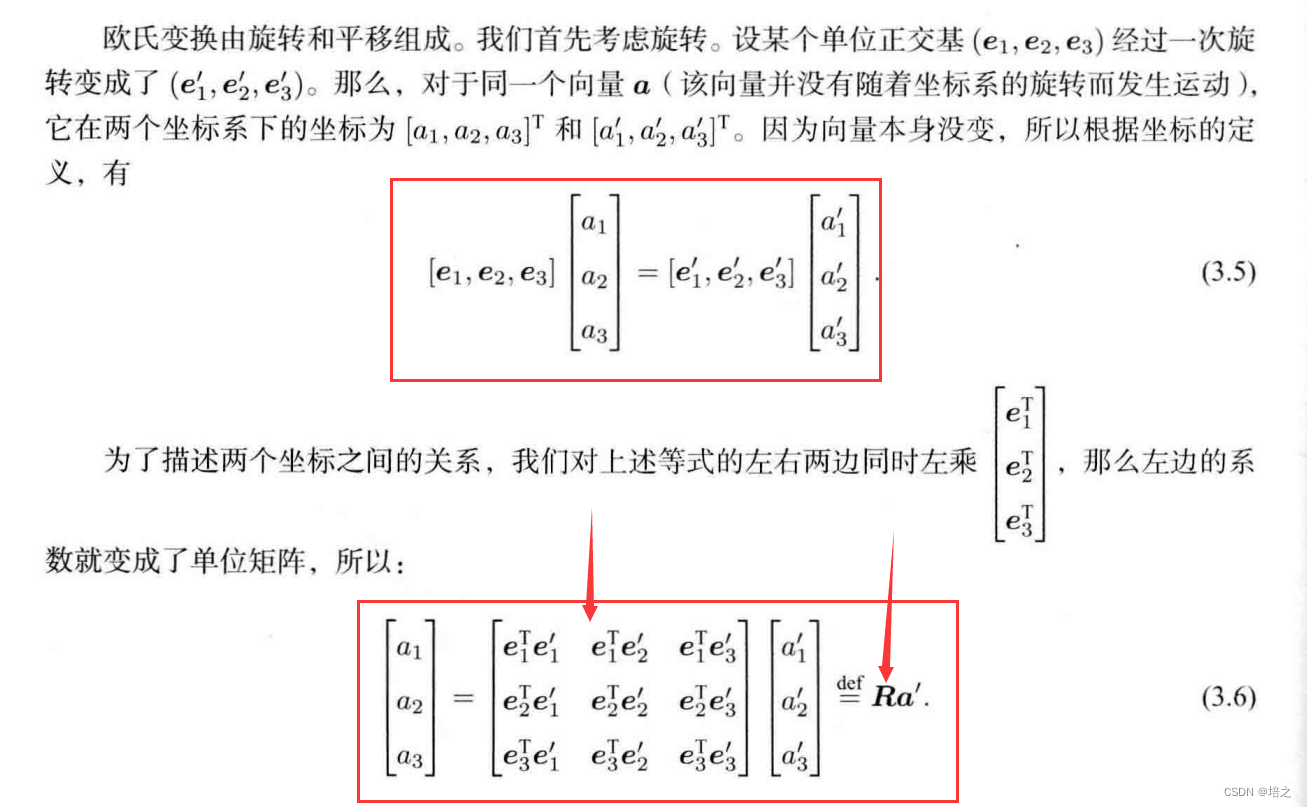
所以,我们需要验证矩阵
R
=
[
e
1
T
e
1
′
e
1
T
e
2
′
e
1
T
e
3
′
e
2
T
e
1
′
e
2
T
e
2
′
e
2
T
e
3
′
e
3
T
e
1
′
e
3
T
e
2
′
e
3
T
e
3
′
]
R = \begin{bmatrix} e_1^{T}e_1^{'}&& e_1^{T}e_2^{'} && e_1^{T}e_3^{'}\\ e_2^{T}e_1^{'}&& e_2^{T}e_2^{'} && e_2^{T}e_3^{'}\\ e_3^{T}e_1^{'}&& e_3^{T}e_2^{'} && e_3^{T}e_3^{'}\\ \end{bmatrix}
R=
e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′
是正交矩阵,
那么我们只需要验证矩阵 R 的转置是他的逆就可以了。
R
T
=
[
e
1
’
T
e
1
e
1
‘
T
e
2
e
1
’
T
e
3
e
2
‘
T
e
1
e
2
‘
T
e
2
e
2
‘
T
e
3
e
3
’
T
e
1
e
3
’
T
e
2
e
3
’
T
e
3
]
R^T=\begin{bmatrix} e_1^{’T}e_1^{}&& e_1^{‘T}e_2^{} && e_1^{’T}e_3^{}\\ e_2^{‘T}e_1^{}&& e_2^{‘T}e_2^{} && e_2^{‘T}e_3^{}\\ e_3^{’T}e_1^{}&& e_3^{’T}e_2^{} && e_3^{’T}e_3^{}\\ \end{bmatrix}
RT=
e1’Te1e2‘Te1e3’Te1e1‘Te2e2‘Te2e3’Te2e1’Te3e2‘Te3e3’Te3
R
T
R
=
[
e
1
’
T
e
1
e
1
T
e
1
’
+
e
1
’
T
e
2
e
2
T
e
1
’
+
e
1
’
T
e
3
e
3
T
e
1
’
e
1
’
T
e
1
e
1
T
e
2
’
+
e
1
’
T
e
2
e
2
T
e
2
’
+
e
1
’
T
e
3
e
3
T
e
2
’
−
−
−
−
−
−
−
]
R^{T}R=\begin{bmatrix} e_1^{’T}e_1^{}e_1^{T}e_1^{’}+ e_1^{’T}e_2^{}e_2^{T}e_1^{’}+ e_1^{’T}e_3^{}e_3^{T}e_1^{’}&& e_1^{’T}e_1^{}e_1^{T}e_2^{’}+ e_1^{’T}e_2^{}e_2^{T}e_2^{’}+ e_1^{’T}e_3^{}e_3^{T}e_2^{’} && -\\ -&& - && -\\ -&& - && -\\ \end{bmatrix}
RTR=
e1’Te1e1Te1’+e1’Te2e2Te1’+e1’Te3e3Te1’−−e1’Te1e1Te2’+e1’Te2e2Te2’+e1’Te3e3Te2’−−−−−
需要证明:
e
1
’
T
e
1
e
1
T
e
1
’
+
e
1
’
T
e
2
e
2
T
e
1
’
+
e
1
’
T
e
3
e
3
T
e
1
’
=
1
(1)
e_1^{’T}e_1^{}e_1^{T}e_1^{’}+ e_1^{’T}e_2^{}e_2^{T}e_1^{’}+ e_1^{’T}e_3^{}e_3^{T}e_1^{’}=1 \tag{1}
e1’Te1e1Te1’+e1’Te2e2Te1’+e1’Te3e3Te1’=1(1)
根据向量內积的性质,有:
e
1
’
T
e
1
e
1
T
e
1
’
+
e
1
’
T
e
2
e
2
T
e
1
’
+
e
1
’
T
e
3
e
3
T
e
1
’
=
cos
2
a
+
cos
2
b
+
cos
2
c
e_1^{’T}e_1^{}e_1^{T}e_1^{’}+ e_1^{’T}e_2^{}e_2^{T}e_1^{’}+ e_1^{’T}e_3^{}e_3^{T}e_1^{’} =\cos^2 a+\cos^2 b+\cos^2 c
e1’Te1e1Te1’+e1’Te2e2Te1’+e1’Te3e3Te1’=cos2a+cos2b+cos2c
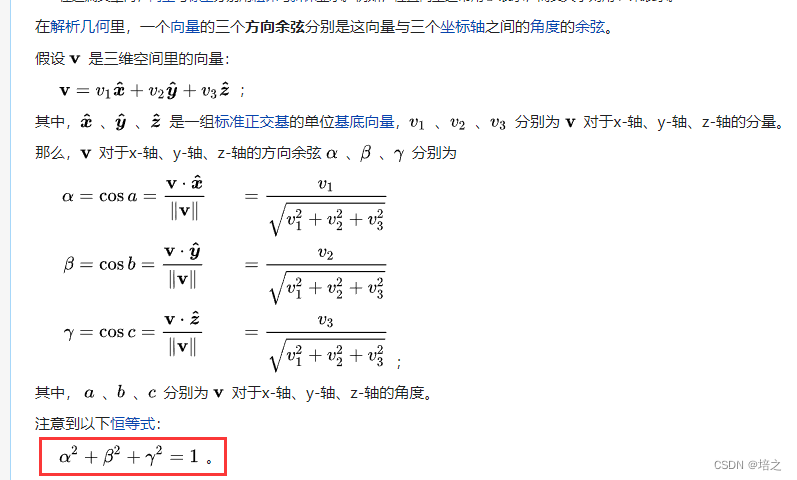
其中
a
,
b
,
c
a,b,c
a,b,c 分别为向量
e
1
′
e_1^{'}
e1′ 与坐标系的三个基底
e
1
,
e
2
,
e
3
e_1^{},e_2^{},e_3^{}
e1,e2,e3所成夹角。由接下来的这张图,易得式(1)成立。
下面要证明:
e
1
’
T
e
1
e
1
T
e
2
’
+
e
1
’
T
e
2
e
2
T
e
2
’
+
e
1
’
T
e
3
e
3
T
e
2
’
=
0
(2)
e_1^{’T}e_1^{}e_1^{T}e_2^{’}+ e_1^{’T}e_2^{}e_2^{T}e_2^{’}+ e_1^{’T}e_3^{}e_3^{T}e_2^{’} = 0 \tag{2}
e1’Te1e1Te2’+e1’Te2e2Te2’+e1’Te3e3Te2’=0(2)
不妨令:
e
1
=
[
1
0
0
]
e
2
=
[
0
1
0
]
e
3
=
[
0
0
1
]
e_1 =\begin{bmatrix} 1 \\ 0\\ 0\\ \end{bmatrix} e_2 =\begin{bmatrix} 0 \\ 1\\ 0\\ \end{bmatrix} e_3 =\begin{bmatrix} 0 \\ 0\\ 1\\ \end{bmatrix}
e1=
100
e2=
010
e3=
001
则
e
1
’
T
e
1
e
1
T
e
2
’
+
e
1
’
T
e
2
e
2
T
e
2
’
+
e
1
’
T
e
3
e
3
T
e
2
’
=
e
1
’
T
(
e
1
e
1
T
+
e
2
e
2
T
+
e
3
e
3
T
)
e
2
’
e_1^{’T}e_1^{}e_1^{T}e_2^{’}+ e_1^{’T}e_2^{}e_2^{T}e_2^{’}+ e_1^{’T}e_3^{}e_3^{T}e_2^{’} = e_1^{’T}(e_1^{}e_1^{T}+e_2^{}e_2^{T}+e_3^{}e_3^{T})e_2^{’}
e1’Te1e1Te2’+e1’Te2e2Te2’+e1’Te3e3Te2’=e1’T(e1e1T+e2e2T+e3e3T)e2’
而
e
1
e
1
T
+
e
2
e
2
T
+
e
3
e
3
T
=
I
e_1^{}e_1^{T}+e_2^{}e_2^{T}+e_3^{}e_3^{T}=I
e1e1T+e2e2T+e3e3T=I
所以 式(2)左边
=
e
1
’
T
I
e
2
’
=
e
1
’
T
e
2
’
=
0
(
正交基旋转之后还是正交基
)
=e_1^{’T}Ie_2^{’}=e_1^{’T}e_2^{’}=0(正交基旋转之后还是正交基)
=e1’TIe2’=e1’Te2’=0(正交基旋转之后还是正交基)
注意,式(1)的证明也可以用式(2)证明的方法。
同理可证矩阵
R
T
R
R^{T}R
RTR 主对角线元素为1,其余元素为0,所以其为单位阵。
同理可证矩阵
R
R
T
RR^{T}
RRT是单位阵。
所以,矩阵 R 是正交矩阵。











![[洛谷-P1273]有线电视网(树形DP + 分组背包DP)](https://img-blog.csdnimg.cn/img_convert/cc40056100e44d8822df1d3284b9ac3b.png)