螺旋矩阵 II

本节对应代码随想录中：代码随想录，讲解视频：一入循环深似海 | LeetCode：59.螺旋矩阵II_哔哩哔哩_bilibili

习题

题目链接：59. 螺旋矩阵 II - 力扣（LeetCode）

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：
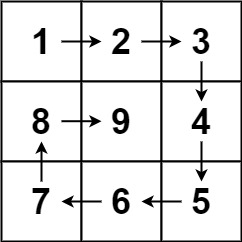
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

我的解法

题目有点像本科时做过的迷宫类题目，数字的增长顺序为右、下、左、上，然后接着按照这个顺序填充。

那么就可以定义一个数组表示每个方向的 x 和 y 应该如何变化，再定义一个 n*n 的数组表示是否访问过当前位置

按照右、下、左、上的顺序去填充矩阵，如果下一个位置在矩阵范围内并且还没有访问过那就填充，否则说明走到头该换方向了，代码如下。

class Solution {
   public:
    vector<vector<int>> generateMatrix(int n) {
        // 4个方向：右下左上
        int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        vector<vector<int>> nums(n,vector<int>(n));
        
        int count = 1;  // 计数
        int x = 0, y = 0, d = 0;    // x和y的坐标,d代表当前方向

        // 是否填充过当前位置
        int isV[n][n];
        for(int i=0; i<n; i++){
            for(int j=0; j<n; j++){
                isV[i][j] = 0;
            }
        }
        // 初始填充[0][0]位置
        nums[0][0]=count;
        isV[0][0]=1;

        while (1) {
            if (count == n * n) {
                break;
            }
            int newX= x + dir[d][0],newY=y + dir[d][1]; // 新的位置
            // 判断新的位置是否符合矩阵范围内并且没有访问过
            if (newX <= n - 1 && newY <= n - 1 && newX >= 0 && newY >= 0 && isV[newX][newY]!=1) {
                x = newX;
                y = newY;
                count++;
                nums[x][y] = count;
                isV[x][y] = 1;

            } else {
                // 到此步，说明走到头了，要改变方向
                d = (d + 1) % 4;
            }
        }
        return nums;
    }
};

看了别人的解法，有几个点可以注意下：

• vector<vector<int>> nums(n,vector<int>(n)); 这种定义会默认全部初始为0，而 int nums[4][4]; 则不会初始为0，需要手动初始化为0
• 二维数组 isV[n][n] 初始化为0时，不必使用双重 for 循环，可以用 int isV[n][n]={0}; 快速初始化
• while(1) 可以换成 while (count <= n * n)，这样就不用专门去判断 count 是否等于 n*n 然后 break 了

别人的解法

代码随想录中的解法有点复杂了，这里就不分析了，附上在 LeetCode 官方题解评论区下看到的一个不错的题解
来源：59. 螺旋矩阵 II 题解 - 力扣（LeetCode）

我的想法是定义一个方向数组，循环这个方向数组，并且还要用另一个数组记录每个位置是否已经访问过。而这个题解省去了方向数组和定义否访问过的数组的创建过程。直接用4个 for 循环代表4个方向，外层用 while 来判断是否填充到了最后一个位置。

代码中的 up、down、left、right 分别代表着当前需要填充区域的上下左右边界，在向前走一个方向要转弯的时候要改变一下边界的数值

class Solution {
   public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n,vector<int>(n));
        // 分别代表着当前需要填充区域的上下左右边界
        int up = 0, down = n - 1, left = 0, right = n - 1, index = 1;
        while (index <= n * n) {
            // 从左向右赋值
            for (int i = left; i <= right; i++) {
                res[up][i] = index++;
            }
            up++; // 上面的一行赋值后上边界应该下移一行，下同
            // 从上向下赋值
            for (int i = up; i <= down; i++) {
                res[i][right] = index++;
            }
            right--;
            // 从右向左赋值
            for (int i = right; i >= left; i--) {
                res[down][i] = index++;
            }
            down--;
            // 从下向上赋值
            for (int i = down; i >= up; i--) {
                res[i][left] = index++;
            }
            left++;
        }
        return res;
    }
};