作者：小树苗渴望变成参天大树
作者宣言：认真写好每一篇博客
作者gitee:gitee

如 果 你 喜 欢 作 者 的 文 章 ，就 给 作 者 点 点 关 注 吧！

---

前言

学习这篇文章之前，最好需要看一下我写的动态内存管理那篇文章link，因为是建立在realloc的基础上再加深对realloc的理解，让我们一起来探索realloc真正的含义

---

一、realloc的原地扩容和异地扩容

我们知道realloc是对已经动态开辟好的内存空间进行扩容，我们是在原来的基础上扩容呢？？还是重新开辟一块空间，再动态内存管理那篇博客，我只带大家画图去理解了一下，这次我将深入内存带大家理解，看看realloc再内存中到底干了什么

例子：

int main()
{
	int* a = (int*)malloc(sizeof(int) * 10);//向空间申请10个整型的空间大小（40个字节）
	int *tmp = (int*)realloc(a, sizeof(int)*20);//扩容到20个整型
	return 0;
}

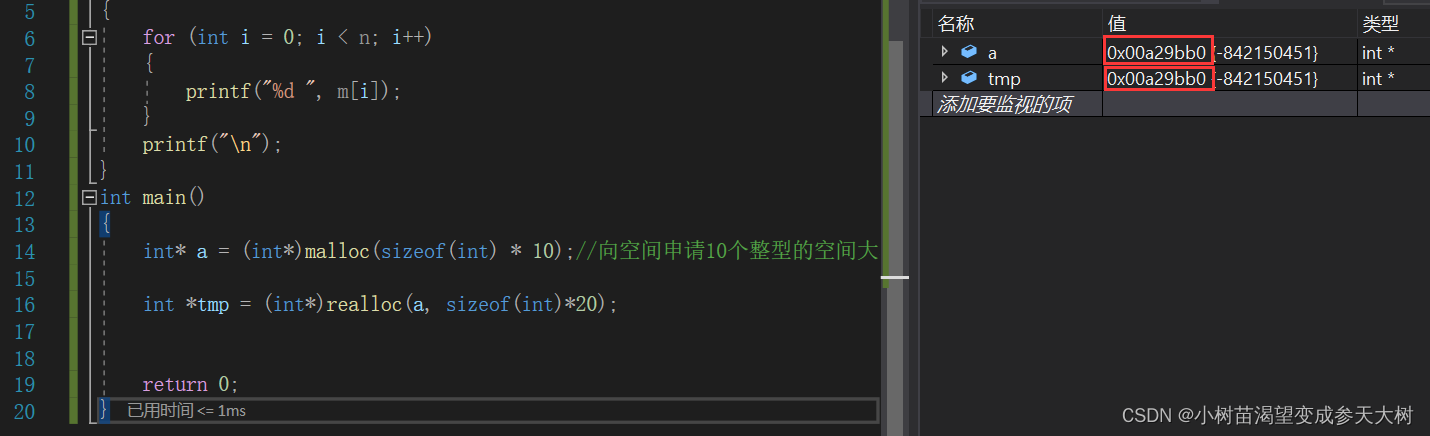
我们看到这两个地址是一样，说明realloc是原地扩容，原因是原来地址的后面空间足够realloc继续往后面扩展，如果我们扩容的空间较大呢？？

int main()
{
	int* a = (int*)malloc(sizeof(int) * 10);//向空间申请10个整型的空间大小（40个字节）
	int *tmp = (int*)realloc(a, sizeof(int)*2000);//扩容到2000个整型
	return 0;
}

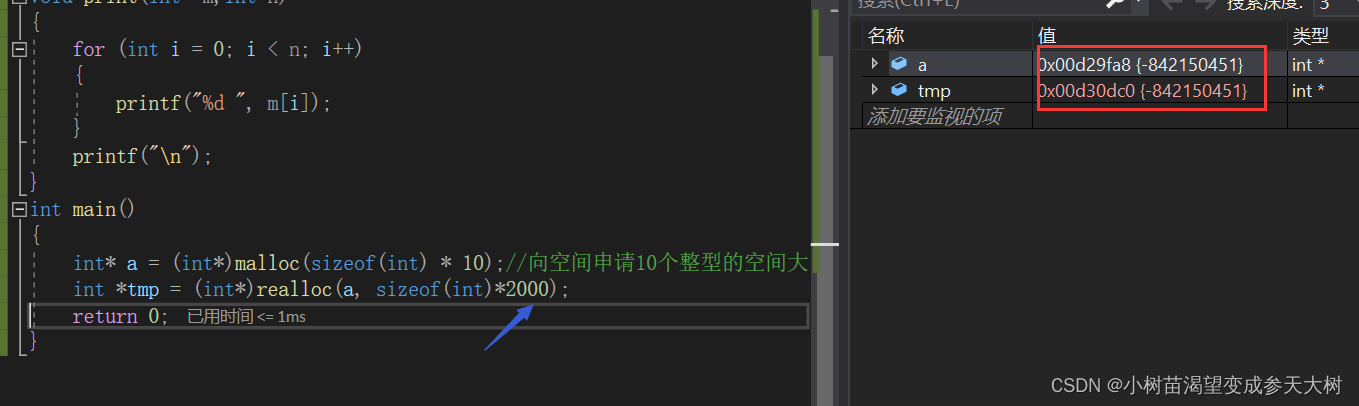
我们看到这是异地扩容，是两块不同的空间地址，所以我们再进行扩容的时候，都是先使用一个变量保存，然后再赋值给原变量，这样防止数据丢失

如果对已经开辟的空间后面进行查看会出现怎样的情况，以及修改里面的数据会出现什么情况？？

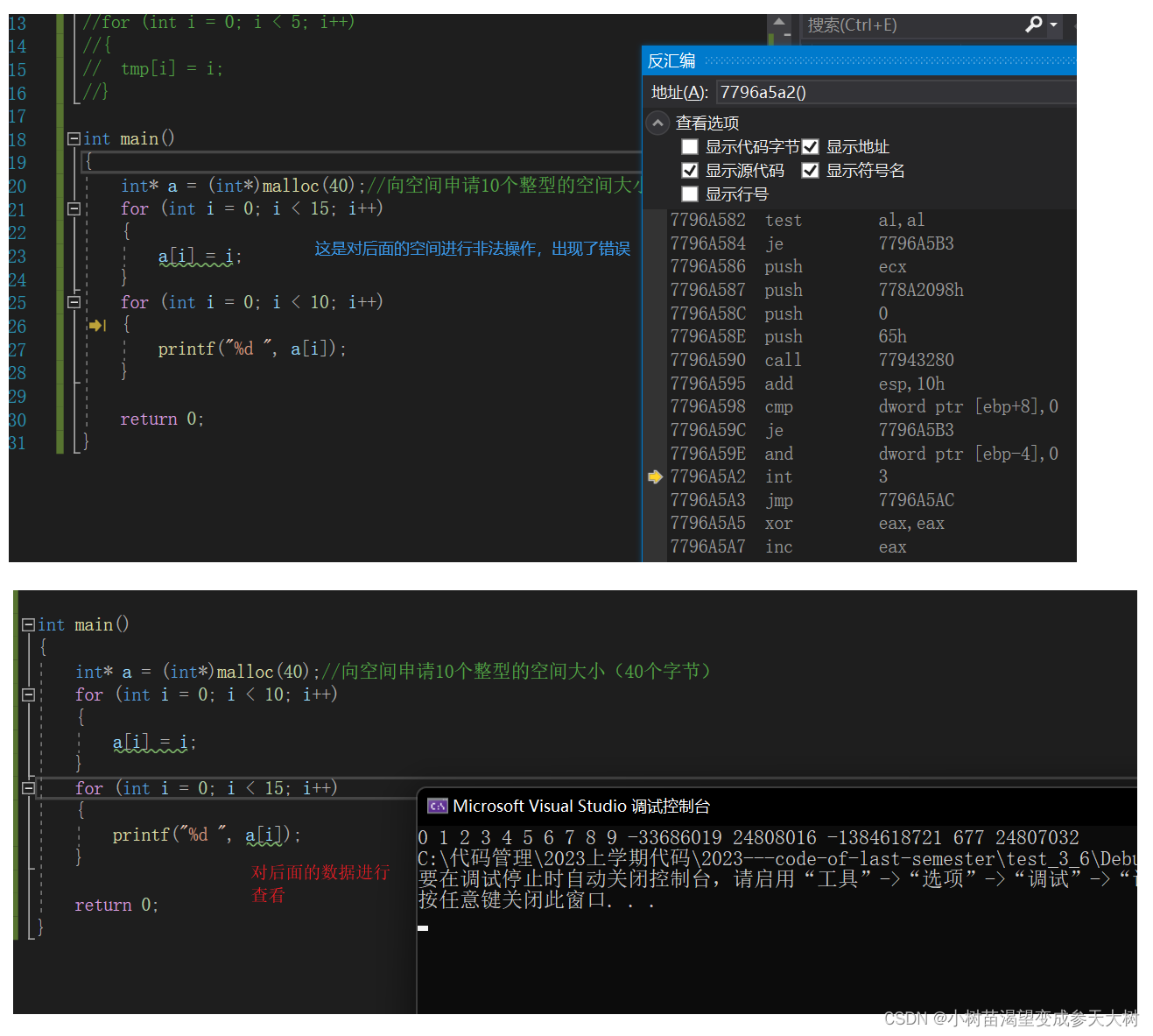
看到这这幅图应该就明白了malloc出来的空间，我们既可以操作也可以查看，后面的空间我们不能操作但是可以访问

二、关于realloc是否可以缩容问题

对于扩容，我的解释是增加空间大小，可以存放更多的数据，对于缩容，表示的是把空间大小减小，变成我们所需要的空间大小，缩容不存在异地缩容，接下来我会定义另一个变量为了区分

我们来看一下这个代码：

int main()
{
	int* a = (int*)malloc(40);//向空间申请10个整型的空间大小（40个字节）
	for (int i = 0; i < 10; i++)
	{
		a[i] = i;
	}
	int *tmp = (int*)realloc(a,20);//缩成5个整型的大小
	for (int i = 0; i < 5; i++)
	{
		tmp[i] = i;
	}
	for (int i = 0; i < 5; i++)
	{
		printf("%d ", tmp[i]);
	} 
	return 0;
}

运行结果：

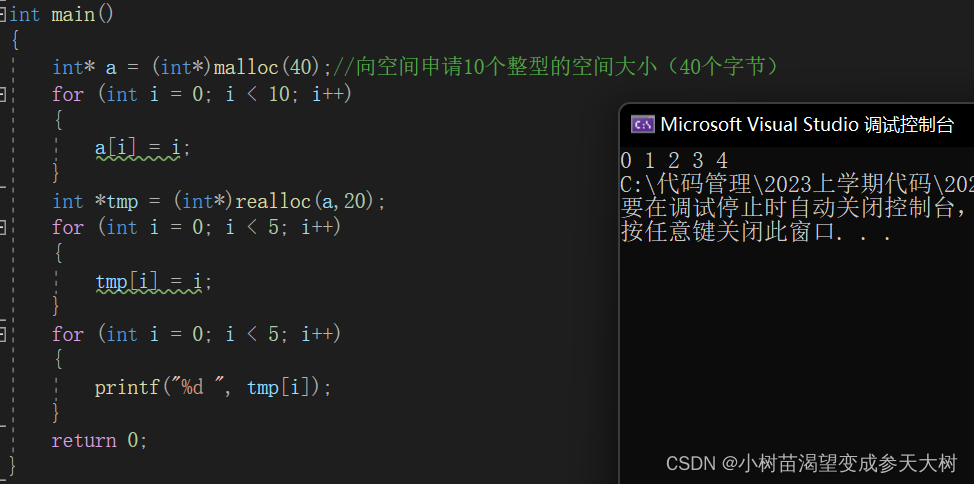
看到这里我相信有部分人会像，这不是可以缩容了吗？有句话叫眼见不一定为真，我们深入内存来看看

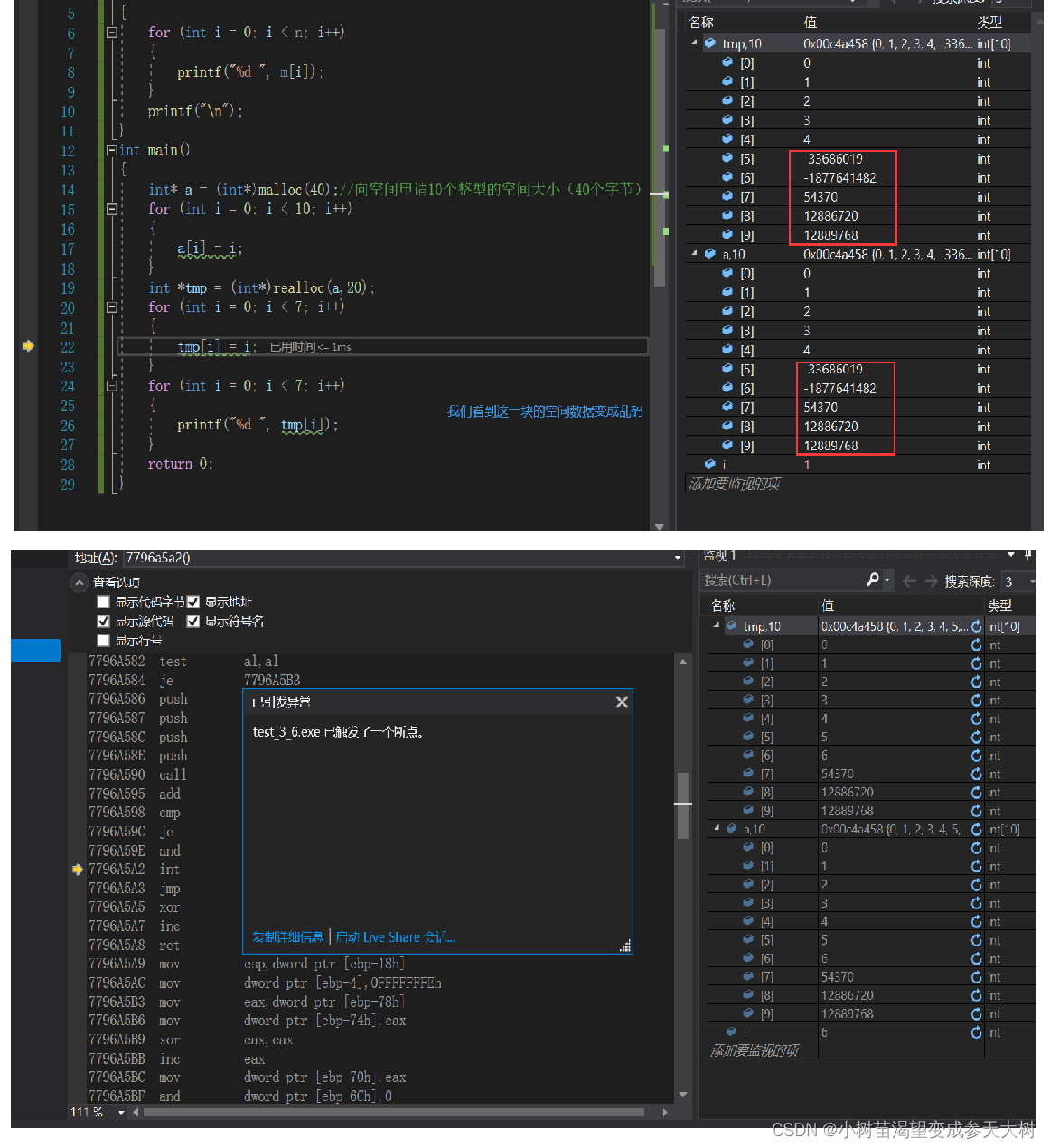
我们看到这个图大致可以明白，出现断点的原因就是出现的野指针的非法访问

我们对tmp进行操作的时候出现了非法访问，很简单，我们缩容了空间变小了，你在往后面访问肯定会出现错误的，那么就是说访问的时候也是会出现非法访问，事实真的是这样吗？我们将tmp后面的数据访问看看会不会报错

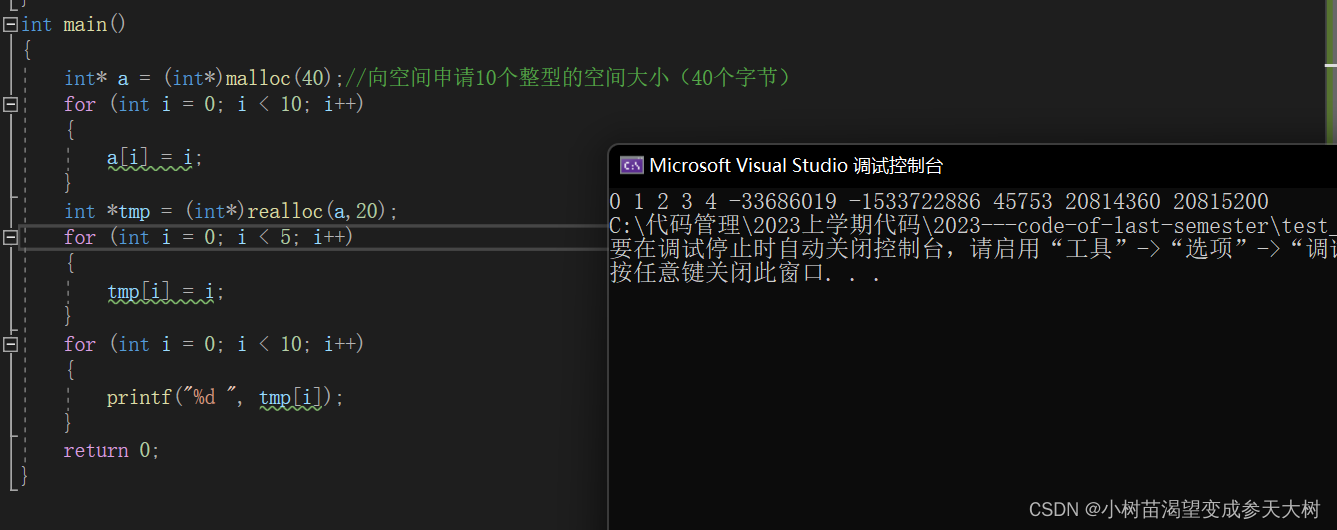
我们上面介绍了不属于我们空间的时候，查看就会出现乱码

在这里我想说起始后面的那块空间实际上只是使用权限不属于我们了，归还给操作系统了，和free不一样，他是把空间都还给操作系统了但是空间还是属于我们的，因为不能操作，所以不能很好给大家看效果，我只能用文字的形式给大家说明

按照我上面的方法确实可以取巧类似于缩容，但是不推荐， 万一你的realloc别人没看到，对后面的数据进行修改出现错误呢？别人默认realloc只做扩容的任务，你突然来个缩容，难免会弄成消化。

我们缩的仅仅只是使用权限，空间还是没有减少的，希望大家可以更好的理解一下

那我们今天的只是分享就先到这里结束了，期待我的下一篇和大家见面