目录
- 1 问题定义
- 2 算法步骤
- 3 代码
- 4 效果
1 问题定义
本博客以最小化问题为例
f
1
=
x
2
f
2
=
(
x
−
2
)
2
min
f
=
(
f
1
(
x
)
,
f
2
(
x
)
)
\begin{aligned} f_1 & = x ^2 \\ f_2 & = (x - 2) ^2 \\ \min f & = (f_1(x), f_2(x)) \end{aligned}
f1f2minf=x2=(x−2)2=(f1(x),f2(x))
代码
def func1(population):
res = population[:, 0] ** 2
return res
def func2(population):
res = (population[:, 0] - 2) ** 2
return res
2 算法步骤

- E P EP EP:外部种群,大小一般为 10 ∗ s i z e 10 * size 10∗size( s i z e size size是种群大小)
- λ \lambda λ:权重向量,本文所提到的权重向量需要均匀分布,可以用numpy正态分布产生。
- z z z:是当代种群,每个目标的最小值
- B ( i ) B(i) B(i):当前点的邻居索引,邻居的计算使用欧氏距离,可以调用sklearn中的库完成
- g t e ( x ∣ λ j , z ∗ ) = max { λ i j ∣ f i ( x ) − z ∗ ∣ } g^{te}(x|\lambda ^j, z^*) = \max\{\lambda_i^j|f_i(x) - z^*|\} gte(x∣λj,z∗)=max{λij∣fi(x)−z∗∣},其中 1 ≤ i ≤ m 1 \leq i \leq m 1≤i≤m(切比雪夫)
因为本博客以最小化问题为例,而原论文则是求解最大化问题,因此上方图片中要做如下修改
Step 2.3中的 z j > f j ( y ′ ) z_j > f_j(y') zj>fj(y′)
注意:当目标数m<=2时适合用切比雪夫
3 代码
import numpy as np
import pandas as pd
from geatpy.core.ndsortESS import ndsortESS # 非支配排序
from sklearn.neighbors import NearestNeighbors # K近邻分类器
from geatpy.operators.mutation.Mutpolyn import Mutpolyn # 多项式变异
from geatpy.operators.recombination.Recsbx import Recsbx # 模拟二进制交叉
from geatpy.visualization.PointScatter import PointScatter # 画图
from untils.SCH import func1, func2
# 通过Euclidean distance产生近邻
def get_neighbor(matrix, n_neighbors = 2):
nbrs = NearestNeighbors(n_neighbors=n_neighbors, algorithm='kd_tree', metric='euclidean').fit(matrix)
distances, indices = nbrs.kneighbors(matrix)
return indices # 返回邻居索引
# 在邻居集合里挑选两个邻居, 返回邻居索引
def select_neighbor(neighbor_indexs, prob_neighbor = 0.9):
indices = []
for index in neighbor_indexs:
if len(indices) > 2: break
probability = np.random.rand()
if probability < prob_neighbor:
indices.append(index)
if len(indices) == 0:
return neighbor_indexs[0:2]
return indices # 返回邻居索引
# 切比雪夫方法更新邻居解
def update_neighbor(weight_vector, neighbor_func, z, y_func):
# 第一行 对应的为y的相关值
copy_func = np.copy(neighbor_func)
copy_func = np.abs(copy_func - z) # 函数值 - 参考点
te = np.multiply(weight_vector, copy_func) # 叉乘
y_te = np.multiply(weight_vector, np.abs(y_func-z))
row_max = np.max(te, axis=1)
bad_neighbor = []
n = row_max.shape[0]
for i in range(n):
if np.max(y_te) <= row_max[i]: # 需要对邻居更新
bad_neighbor.append(i)
return bad_neighbor
def update_external_population(pop, func, y, y_func): # pop: 外部种群;func: 外部种群函数值
if pop is None:
pop = y
func = y_func
else:
pop = np.row_stack((pop, y))
func = np.row_stack((func, y_func))
levels, criLevel = ndsortESS(func)
levels = levels.astype('i4') # float -> int
pd_levels = pd.DataFrame(levels) # numpy -> pandas
rank_group = pd_levels.groupby(0).groups # 等级分组
best_rank = rank_group[1].values # 最好等级的所有下标
pop = pop[best_rank, :]
func = func[best_rank, :]
if func.shape[0] > K * size:
r = np.random.randint(0, K * size, 1)
pop = np.delete(pop, r, axis=0)
func = np.delete(func, r, axis=0)
return pop, func
if __name__ == '__main__':
size = 50 # 种群大小
dim = 2 # 目标函数的个数
n = 1 # 决策变量的个数
n_neighbor = 50 # 权重向量近邻的个数
lb = np.full(n, -10) # 自变量下限
ub = np.full(n, 10) # 自变量上限
varTypes = np.full(n, 0) # 离散 or 连续
iteration = 250 # 迭代次数
K = 2 # 外部种群大小 = K * size
np.random.seed(1)
# ===================== 产生均匀分布的权重向量 =======================
weight_vector = np.random.randn(size, dim)
ss = np.sum(weight_vector, axis=1)
for k in range(dim):
weight_vector[:, k] = weight_vector[:, k] / ss
# ===================== 产生均匀分布的权重向量 =======================
all_neighbor = get_neighbor(weight_vector, n_neighbor)
# ========================= 产生随机种群 ===========================
x = np.random.uniform(lb, ub, (size, n))
func = np.column_stack((func1(x), func2(x)))
ideal_points = np.min(func, axis=0) # 所有函数值的最小值,即理想点
# ========================= 产生随机种群 ===========================
exter_pop = None # 外部种群
exter_obj = None # 外部种群函数值
PS = PointScatter(dim, True, True, "MOEA/D", ['F1', 'F2', 'F3'], saveName=None)
for i in range(iteration):
print(i)
for s in range(size):
# ========================= 挑选两个邻居 ==========================
neighbor = all_neighbor[s, :] # 当前个体的邻居索引
two_neighbor = np.random.choice(neighbor, size = 2, replace=False)
neighborsX = x[two_neighbor, :]
# ========================= 挑选两个邻居 ==========================
# ======================== 进行交叉变异操作 =========================
recsbx = Recsbx(XOVR=1, Half_N=True, n=20, Parallel=True) # 交叉
y = recsbx.do(neighborsX)
mutation = Mutpolyn(Pm=1/n, DisI=20) # 变异
y = mutation.do(Encoding='RI', OldChrom=y, FieldDR=np.array([lb, ub, varTypes]))
# ======================== 进行交叉变异操作 =========================
# ============================= 更新z ==============================
y_func = np.column_stack((func1(y), func2(y)))
for d in range(dim):
ideal_points[d] = np.minimum(ideal_points[d], y_func[0, d])
# ============================= 更新z ==============================
# =========================== 更新邻居解 ============================
weight_vector_neighbor = weight_vector[neighbor, :] # 邻居的权重向量
neighborsFunc = func[neighbor, :] # 邻居的函数矩阵
bad_neighbor = update_neighbor(weight_vector_neighbor, neighborsFunc,ideal_points, y_func)
x[bad_neighbor, :] = y
func[bad_neighbor, :] = y_func
# =========================== 更新邻居解 ============================
# =========================== 更新外部种群 ============================
exter_pop, exter_obj = update_external_population(exter_pop, exter_obj, y, y_func)
# =========================== 更新外部种群 ============================
right_label = 'size: ' + str(K * size) + '\n' + 'iteration: ' + str(iteration)
PS.add(exter_obj, color='purple', label=right_label)
PS.draw()
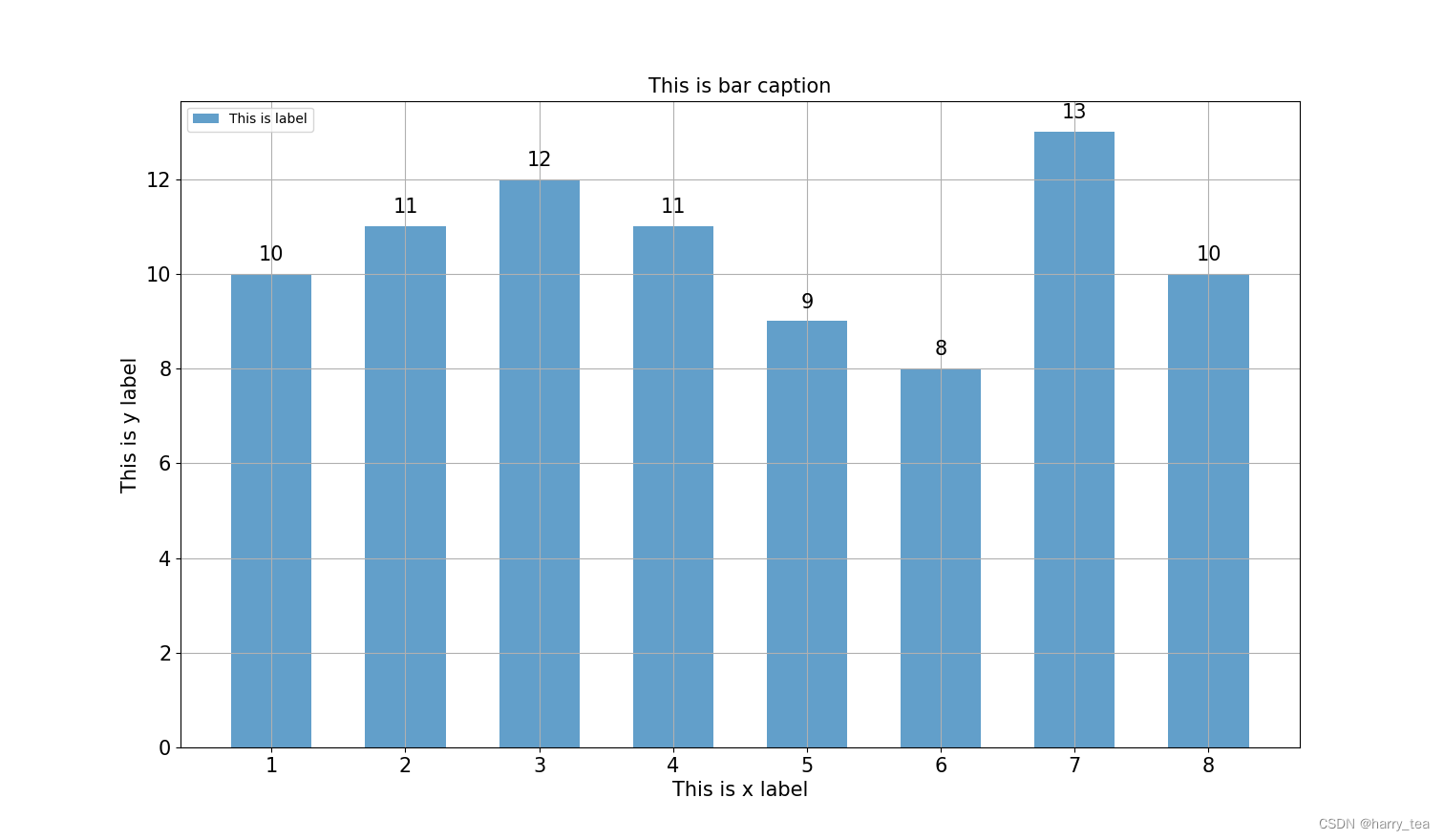
4 效果