A

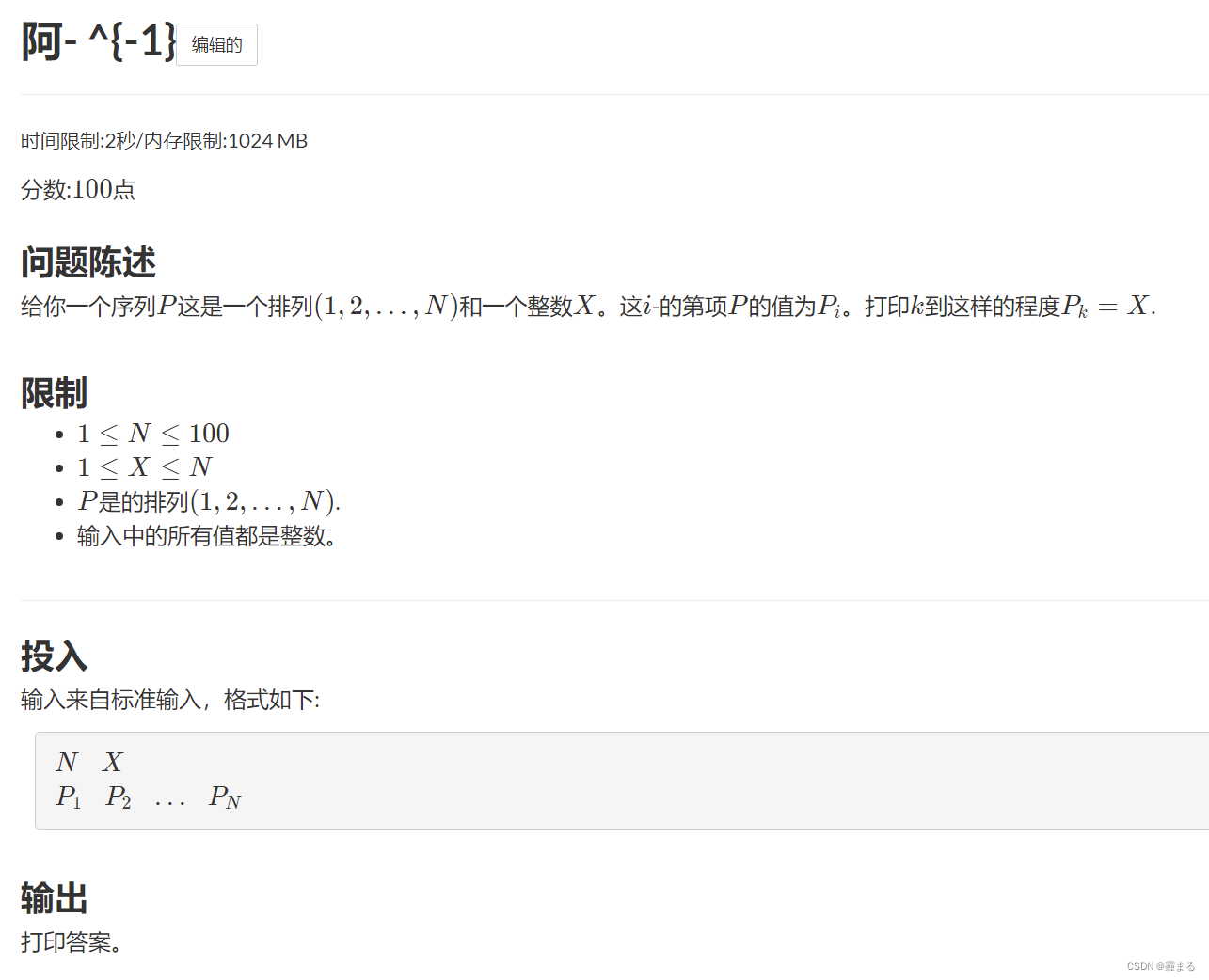
题意

给出一个排列和X
问X在排列中出现的下标是多少

代码

void solve()
{
    cin>>n>>m;
    for(ll i=1;i<=n;i++) 
    {
        cin>>arr[i];
        if(arr[i]==m) ans=i;
    }
    cout<<ans<<endl;
    return;
}

B题

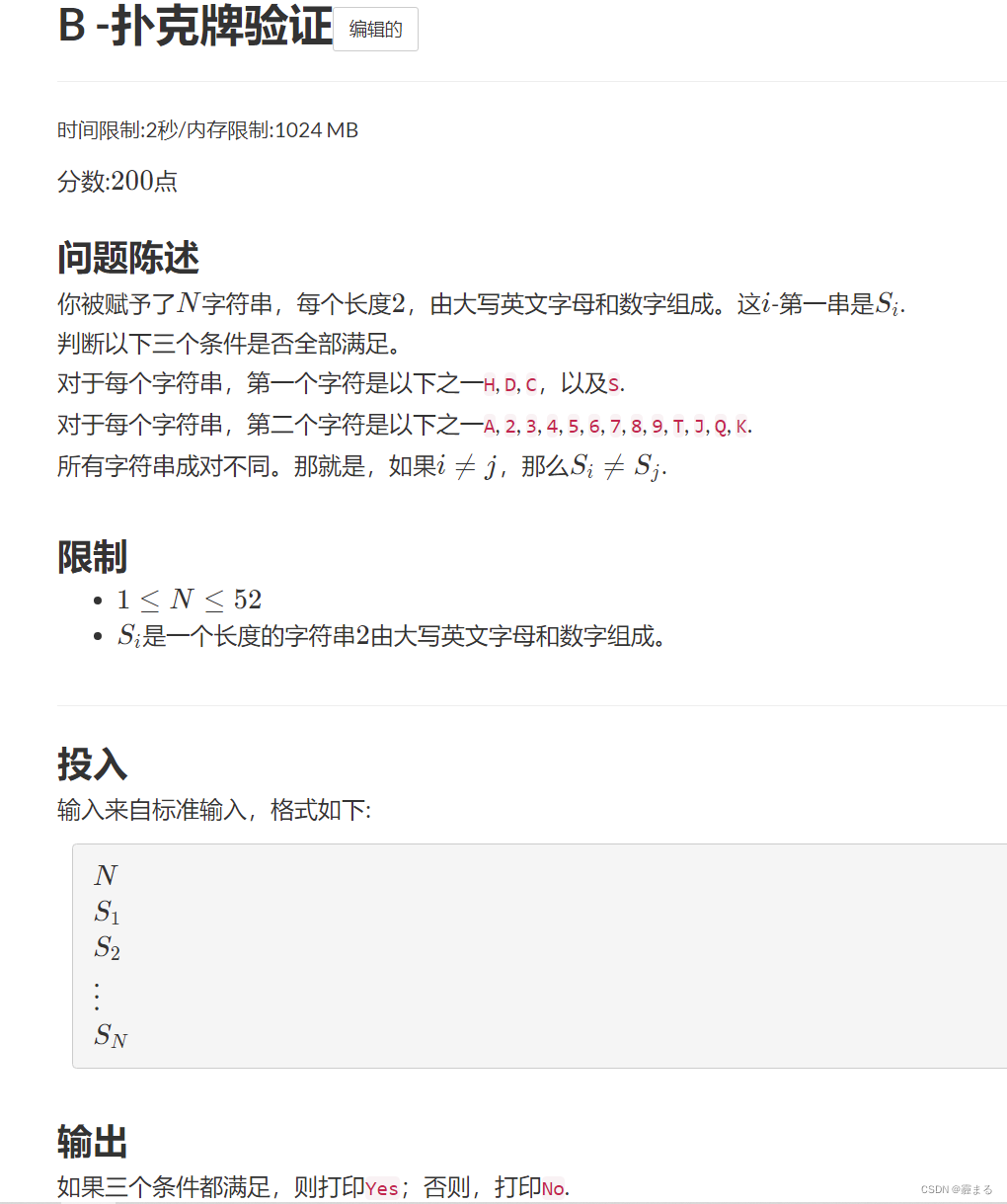
题意

这机翻翻译的挺正确的, 题意也挺明白感觉没必要解释

代码

void solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>s[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            if(i!=j&&s[i]==s[j])
            {
                cout<<"No"<<endl;
                return;
            }
        }
    }
    string f="HDCS";
    string se="A23456789TJQK";
    for(int i=1;i<=n;i++)
    {
        char c=s[i][0];
        ans=0;
        for(int j=0;j<f.size();j++)
            if(c==f[j]) ans=1;
        if(ans==0)
        {
            cout<<"No"<<endl;
            return;
        }
        ans=0;
        c=s[i][1];
        for(int j=0;j<se.size();j++) 
            if(c==se[j]) ans=1;
        if(ans==0)
        {
            cout<<"No"<<endl;
            return;
        }
    }
    cout<<"Yes"<<endl;
    return;
}

C

题意

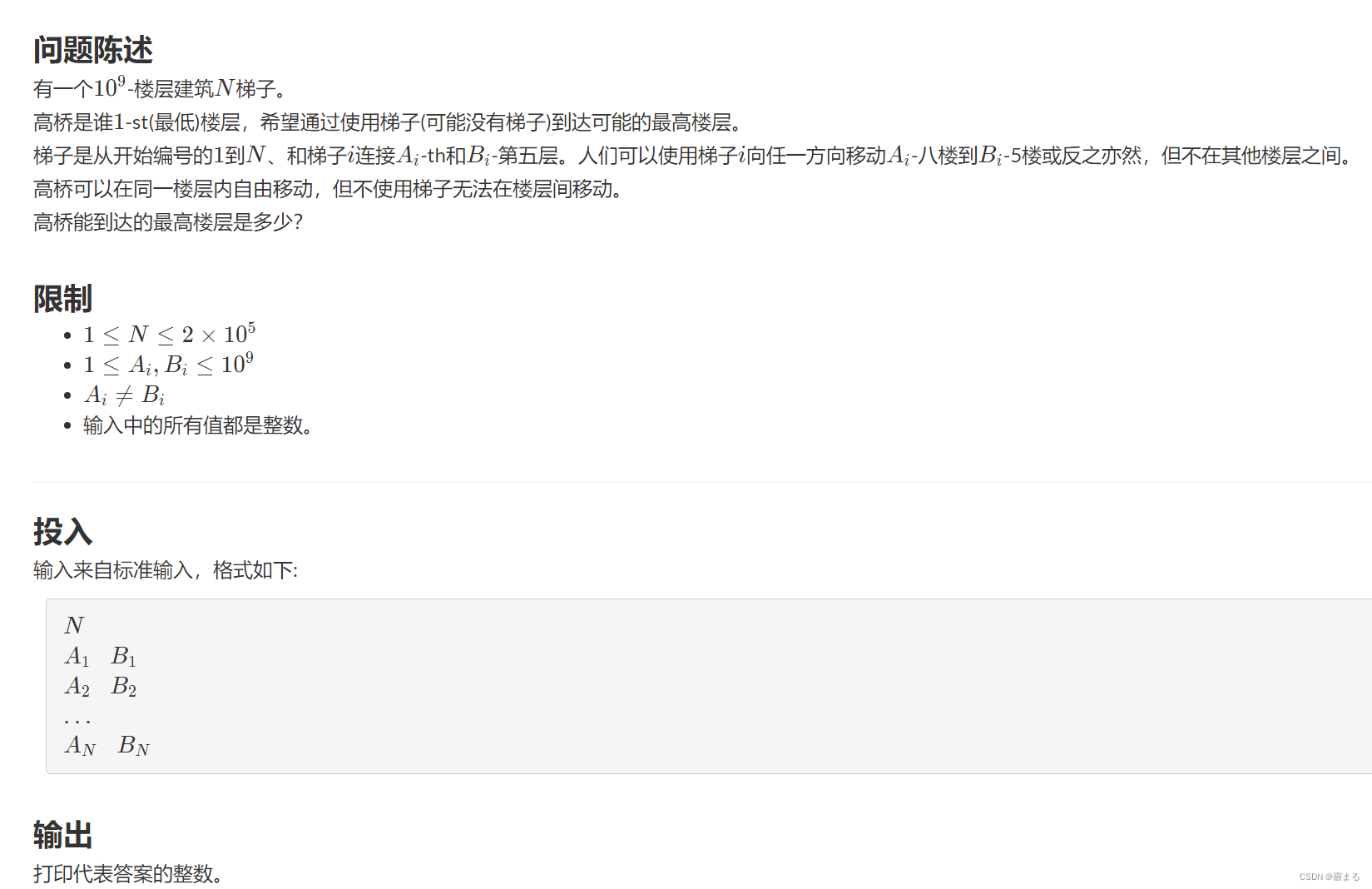
给出N个梯子, 梯子的起点是A和B, 梯子可以从上走到下也可以从下走到上, 起点在1, 问能到的最高楼层是哪个

题解

dfs剪枝
不剪枝会T
将整个建筑看做成一个图, 每个梯子都是无向边
然后遍历一遍图就好了, 需要注意, 对于叶子结点不进行搜索(剪枝)

代码

void dfs(ll x)
{
    ans=max(ans,x);
    dist[x]=1;

    for(auto it:mp[x])
    {
        ans=max(it,ans);
        if(it>=1&&dist[it]==0&&mp.count(it))
            dfs(it);
    }
}

void solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        ll x,y;
        cin>>x>>y;
        mp[x].push_back(y);
        mp[y].push_back(x);
    }
    ans=0;

    dfs(1);

    cout<<ans<<endl;
    return;
}

D题

题意

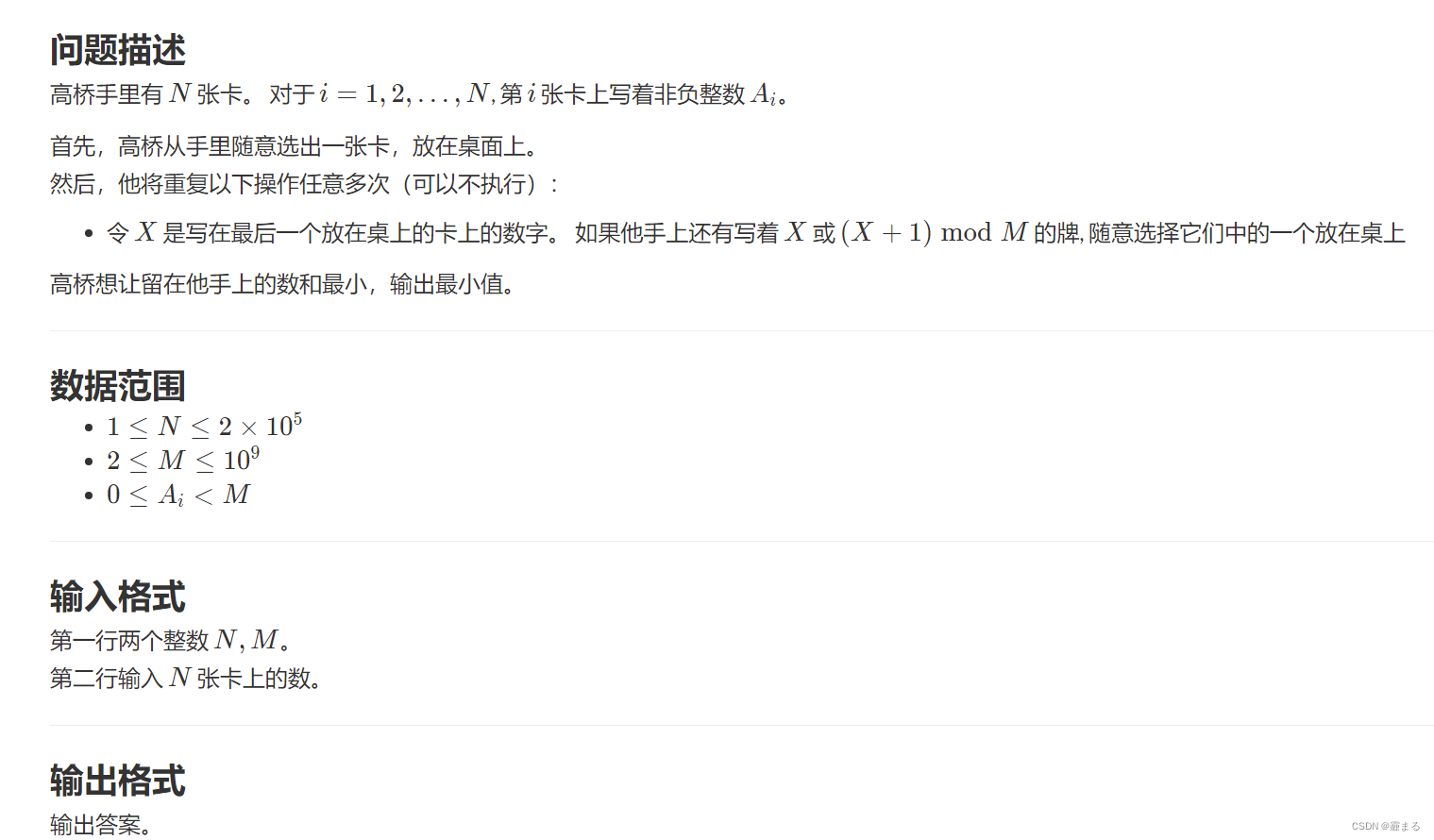
N张卡上每张卡都有Ai分数
首先可以随意抽出一张卡放在桌面上
定义X为上一张放在桌面上的卡的分数
然后可以不断放下和X分数相同或者(X+1)%mod分数的卡牌
问如何使得最后留在手上的卡的分数总和最小

题解

先对序列进行排序
很明显我们只能选择一整段相等且连续的子串
按照题意, 肯定是贪心总和最长的子串
暴力算总和肯定会t, 这题还是环状的处理起来感觉还挺麻烦的, 但其实也就mod一下的程度
对数组进行排序之后按照题意要放下和X分数相同或者(X+1)%mod的分数的卡牌
因为这题是环状的, 所以需要将if arr[pos]==arr[pos+1]的操作改为if arr[pos]==arr[(pos+n-1)%n], 这样就能解决掉环状的问题, 接下来找到每一段子串的分数总和找出最大值即可

代码

void solve()
{
    cin>>n>>m;
    vector<ll>arr(n);
    for(int i=0;i<n;i++) 
        cin>>arr[i];

    sort(arr.begin(),arr.end());

    ll a_sum=accumulate(arr.begin(),arr.end(),0ll);

    vector<ll>none(n,0);

    ll l,r;
    l=0,r=0;
    ans=a_sum;

    while(!none[l])
    {
        none[l]=1;
        ll sum=arr[l];
        r=(l+1)%n;
        while(l!=r&&(arr[r]==arr[(r+n-1)%n]||arr[r]==(arr[(r+n-1)%n]+1)%m))
        {
            sum+=arr[r];
            r++;
            r%=n;
        }
        ans=min(ans,a_sum-sum);
        l=r;
    }

    cout<<ans<<endl;

    return;
}