2022年第十二届MathorCup高校数学建模
A题 大规模指纹图像检索的模型与实现
原题再现
在生物特征识别领域,指纹作为最具独特性与持久性的生物特征之一,被广泛应用于身份识别。
指纹识别过程分为特征提取和比对两个环节。其中特征提取环节会提取用于指纹识别的指纹特征,一般国际上最为常见的指纹特征为“细节点”特征,其可视化展示形式如图 1 中的浅蓝色小圆圈及对外伸出的浅蓝色短线段,短线段用于指示细节点处纹线方向。细节点一般采用三元存储格式:(x,y,θ),分别表示 x 轴像素坐标、y 轴像素坐标及细节点方向。一般而言:(1)指纹图像坐标体系:左上角为坐标原点,且 x 轴方向向右,y 轴方向向下;(2)细节点表达约定:细节点 x, y 的位置采用指纹图像坐标系表达,其方向规定:零度方向为 x 轴正方向(向右),90 度方向为 y 轴负方向(向上),180 度方向为 x 轴负方向(向左),270 度方向为 y 轴正方向(向下),最大角度为 359 度。角度的最小区分单位为 1 度。

在指纹匹配环节,需要对两幅指纹图像的“同一性”进行定量评价,通常采用相似度指标。常见的两枚指纹之间的相似度评价主要依据每枚指纹图像中各个细节点之间的匹配关系。如图 1 所示,相互具有匹配关系的细节点之间用一根跨越两幅图像的红线将其互相连接,用于可视化展示。
在指纹图像匹配环节,常需要考虑如下的情况:
考虑到在采集指纹图像时,手指按压图像采集设备的角度、轻重及位置各不相同,因此两幅指纹图像需要做图像的旋转、平移后才能相互对准。由于手指皮肤较为柔软,通过按压方式采集到的指纹图像会发生一定程度的不规则弹性形变,在图 1 中会发现两幅指纹图像中,某些相互匹配的细节点在对准时,不能完全“重叠”,有一定幅度的位置及角度的偏差。这一现象也可以从“跨越两幅图像的红线并不是都平行”现象中观察到。
考虑到手指可能存在临时性蜕皮、褶皱等因素,且空气中的湿度及皮肤表面的干燥程度或粘附在皮肤上的异物等都会导致采集到的指纹图像存在纹线模糊、遮挡等现象,最终导致某些原本应该提取到的特征没有提取到,或者提取了一定数量的伪特征。在图 1 中可以观察到并不是所有的细节点都有对应的红线进行关联。
指纹识别问题中有一种一对多比对模式(one-to-many matching),是录入的查询指纹与指纹数据库中的所有已登记指纹逐一进行匹配,直至找到相似度最佳的已登记指纹或搜索完整个指纹数据库后给出无对应已登记指纹的结论。辨识模式主要应用于刑侦指纹自动识别系统、大型指纹考勤系统和门禁系统等。随着社会上指纹识别应用的普及,用于识别人员身份的指纹数据库规模也迅速上升,居民身份证指纹库容甚至达到了亿人级别。这也会导致“逐一”遍历全库的查找方式因每次遍历时间过长而无法具有实际应用价值,必须引入图像检索技术,缩短数据库的每次遍历时间。
指纹图像的检索原理可以形象的看成:用若干大筛子快速、精准地筛除掉数据库中绝大多数与查询指纹图像明确不具有“同一”关系的图像。检索过程完成后,留下的少量图像和查询指纹具有高度相似性,需要进一步利用指纹识别算法做“逐一”识别。
一般而言,图像检索过程筛选掉的指纹图像少,则在检索过程完成后保留下来“同一”关系指纹图像的可能性大,但是整个识别过程的耗时较长;反之,检索算法筛选掉的指纹图像多,则在筛选后保留下来“同一”关系指纹图像的可能性相对变小,但是整个识别过程的耗时较短。若检索过程中筛选掉了“同一”关系的指纹,则后续“逐一”比对算法无论怎么改进都无法再找到这枚“同一”关系的指纹。因此如何设计高效精准的搜索算法是大规模指纹图像检索的关键问题。
问题 1:分析指纹图像的细节点特征(参见附件三所述三个数据文件),给出可用于指纹快速检索的检索方法,请阐述该检索方法的原理。重点说明:(1)检索过程中避免筛除掉“同一”指纹的机制;(2)完整、清晰的图像检索模型框架及实现方法;(3)给出该检索方法的时间复杂度、空间复杂度分析。估算检索方法自身占用的内存空间规模及由于采用该检索方法,每一枚指纹图像需要承担的内存空间大小。
问题 2:针对提出的检索方法:将数据文件中提供的具有“同一”关系的全部指纹对子(TZ_同指.txt)作为查询图像在指纹数据集中进行检索方法验证。具体要求参见附件一。
问题 3:针对 TZ_同指 200_乱序后_Data.txt 数据文件采用和问题 2 相同的方式进行检索,给出检索结果,并将结果数据压缩为.zip 格式后上传到竞赛系统的计算结果中。具体要求参见附件二。
问题 4:(1)在完成本赛题时你们可能尝试了不同类型的数学模型及技术路线,并利用问题 2 的数据验证、优选出最佳的检索方法。请介绍并评价你们所考虑过的模型及技术路线的优缺点;(2)本赛题最高的筛选量为 97%,针对 97%以上的筛选量,你们在检索精度、检索时间及内存占用等方面有什么更好的改进策略或者会尝试什么新的检索方法?
整体求解过程概述(摘要)
生物识别领域中,指纹识别被广泛应用,指纹筛选和识别的问题受到广泛关注。对于指纹的筛选过程,筛选算法的设定尤为重要。
针对问题 1,本文利用指纹图像的特征点坐标,将指纹图像进行分割为多个子空间。统计每个子空间内的特征点坐标,用来计算该子空间下的特征,并将所有子空间的坐标信息组合为该指纹的特征向量,利用 K-mean 聚类法,以特征向量为聚类标准,使用欧氏距离对指纹数据集进行聚类。在查询过程中,计算查询指纹的特征值,再与数据库中不同的子类中心坐标进行比对,确定距离最小的几个子类作为该查询指纹在数据库筛选的结果。在只使用特征向量进行检索的情况下,在 80%,90%,95%,97%筛选的条件下,穿透率分别为 80%、76%、64%和 36%。当需要筛选掉较多的指纹数据时,针对上述方法快速但容易泄露“同一”指纹的情况,本题利用特征向量预先筛选出一定的指纹,并对筛选出的指纹一一对比,确定相似程度最高的部分指纹作为筛选结果。通过引入第二次筛选,可以极大提升检索结果,同时避免遍历数据库的问题。
将问题 1 中的算法应用于问题 2,并考虑到指纹数据收集的不稳定性,在二次筛选前进行指纹图片的校正。对于筛选算法,我们比较了利用欧氏距离、利用 BP 神经网络以及使用极坐标下增设自适应误差窗口判断不同图像中任意两个特征点的相似度。结果表明,对于本文的数据,使用简单的欧氏距离可以达到较好的效果,在 80%,90%,95%,97%筛选量的情况下,结果分别为 93.7%、88.7% 、84%、和 80.3%。而利用BP 神经网络和自适应误差窗口较差且需要较大的计算量。再将问题 2 的方法应用于问题 3 得出问题 3 的检索结果。
提出的二次检索模型可以兼顾时间和检索效率,首先快速筛选掉大量不相关的样本,再通过逐一匹配得到高质量的筛选数据。对于 97%即以上的筛选量,单一的筛选方式几乎无法满足要求,因此需要不同的检索方式进行组合:先进行大量样本的筛除,之后利用精确度较高的算法进行继续筛选,直至达到要求。对于每一个步骤中的筛选,可以结合多个筛选方式,以集成学习投票的方式筛选目标样本,避免单一因素的影响。
模型假设:
假设 1:所有数据来源于附件,TZ_同指.txt 全部 500 个匹配对子(合计1000 行)的数据均为真实的采样数据,且三组数据符合相同或者相似的分布,数据之间没有较大的差别。
假设 2: 数据部分受脱皮等其他情况的影响,但不损坏整体的指纹特征或整体指纹特征受异常情况的影响的数据量很少。
假设 3:所有来自文件的指纹特征点能反映指纹的大部分特征,彼此之间相互分散。
总体流程分析:
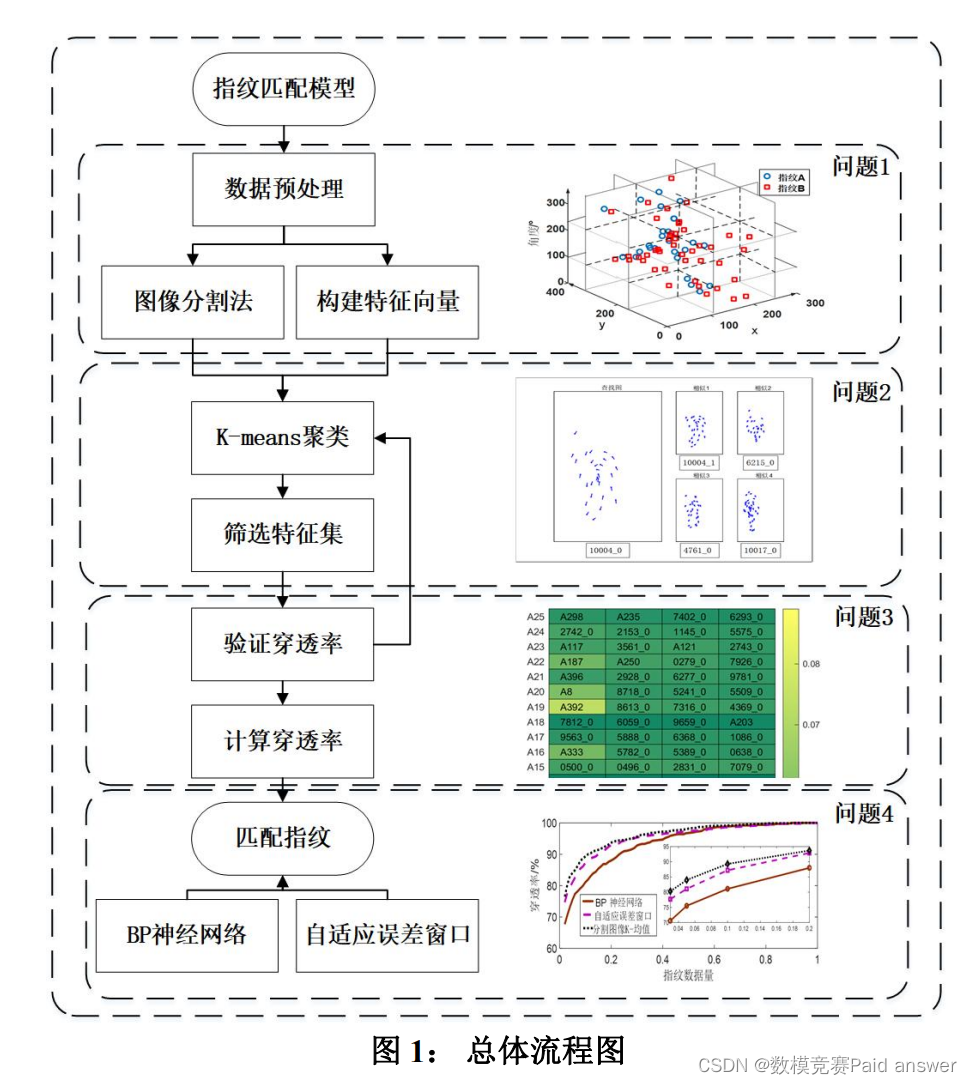
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
The actual procedure is shown in the screenshot
#统计直方图,用load()载入图片的像素pix,再分别读取每个像素点的R\G\B值进行统计(分别为0-255)
#将256个颜色值的统计情况投影到32个,返回R\G\B投影后的统计值数组,共32*3=96个元素
def calc_Hist(img):
'''
#120张图片,4.43s
w,h = img.size
pix = img.load() #载入图片,pix存的是像素
calcR = [0 for i in range(0,32)]
calcG = [0 for i in range(0,32)]
calcB = [0 for i in range(0,32)]
for i in range(0,w):
for j in range(0,h):
(r,g,b) = pix[i,j]
#print (r,g,b)
calcR[r/8] += 1
calcG[g/8] += 1
calcB[b/8] += 1
calcG.extend(calcB)
calcR.extend(calcG)
return calcR
'''
#120张图,3.49s
w,h = img.size
pix = img.load() #载入图片,pix存的是像素
calcR = [0 for i in range(0,256)]
calcG = [0 for i in range(0,256)]
calcB = [0 for i in range(0,256)]
for i in range(0,w):
for j in range(0,h):
(r,g,b) = pix[i,j]
#print (r,g,b)
calcR[r] += 1
calcG[g] += 1
calcB[b] += 1
calcG.extend(calcB)
calcR.extend(calcG) #256*3
#calc存放最终结果,32*3
calc = [0 for i in range(0,96)]
step = 0 #calc的下标,0~95
start = 0 #每次统计的开始位置
while step < 96:
for i in range(start,start+8): #8个值为1组,统计值相加,eg:色彩值为0~7的统计值全部转换为色彩值为0的统计值
calc[step] += calcR[i]
start = start+8
step += 1
#print calc
return calc