提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 1.主成分分析(PCA)方法
- 2.算法步骤
前言
主成分分析(Principal Components Analysis,PCA)是一种数据降维技术,通过正交变换将一组相关性高的变量转换为较少的彼此独立、互不相关的变量,从而减少数据的维数。
为了能准确的研究两个变量在变化过程中的相似程度,我们就要把变化幅度对协方差的影响,从协方差中剔除掉。于是,相关系数就横空出世了,就有了最开始相关系数的公式:
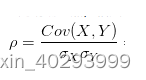
总结一下,对于两个变量X、Y,
当他们的相关系数为1时,说明两个变量变化时的正向相似度最大,即,你变大一倍,我也变大一倍;你变小一倍,我也变小一倍。也即是完全正相关(以X、Y为横纵坐标轴,可以画出一条斜率为正数的直线,所以X、Y是线性关系的)。
随着他们相关系数减小,两个变量变化时的相似度也变小,当相关系数为0时,两个变量的变化过程没有任何相似度,也即两个变量无关。
当相关系数继续变小,小于0时,两个变量开始出现反向的相似度,随着相关系数继续变小,反向相似度会逐渐变大。
1.主成分分析(PCA)方法
主成分分析是最基础数据降维方法,它只需要特征值分解,就可以对数据进行压缩、去噪,应用十分广泛。
主成分分析的目的是减少数据集变量数量,同时要保留尽可能多的特征信息;方法是通过正交变换将原始变量组转换为数量较少的彼此独立的特征变量,从而减少数据集的维数。
主成分分析方法的思想是,将高维特征(n维)映射到低维空间(k维)上,新的低维特征是在原有的高维特征基础上通过线性组合而重构的,并具有相互正交的特性,即为主成分。
通过正交变换构造彼此正交的新的特征向量,这些特征向量组成了新的特征空间。将特征向量按特征值排序后,样本数据集中所包含的全部方差,大部分就包含在前几个特征向量中,其后的特征向量所含的方差很小。因此,可以只保留前 k个特征向量,而忽略其它的特征向量,实现对数据特征的降维处理。
主成分分析方法得到的主成分变量具有几个特点:(1)每个主成分变量都是原始变量的线性组合;(2)主成分的数目大大少于原始变量的数目;(3)主成分保留了原始变量的绝大多数信息;(4)各主成分变量之间彼此相互独立。
2.算法步骤
主成分分析的基本步骤是:对原始数据归一化处理后求协方差矩阵,再对协方差矩阵求特征向量和特征值;对特征向量按特征值大小排序后,依次选取特征向量,直到选择的特征向量的方差占比满足要求为止。
算法的基本流程如下:
(1)归一化处理,数据减去平均值;
(2)通过特征值分解,计算协方差矩阵;
(3)计算协方差矩阵的特征值和特征向量;
(4)将特征值从大到小排序;
(5)依次选取特征值最大的k个特征向量作为主成分,直到其累计方差贡献率达到要求;
(6)将原始数据映射到选取的主成分空间,得到降维后的数据。
在算法实现的过程中,SKlearn 工具包针对实际问题的特殊性,又发展了各种改进算法,例如:
增量主成分分析:针对大型数据集,为了解决内存限制问题,将数据分成多批,通过增量方式逐步调用主成分分析算法,最终完成整个数据集的降维。
核主成分分析:针对线性不可分的数据集,使用非线性的核函数把样本空间映射到线性可分的高维空间,然后在这个高维空间进行主成分分析。
稀疏主成分分析:针对主成分分析结果解释性弱的问题,通过提取最能重建数据的稀疏分量, 凸显主成分中的主要组成部分,容易解释哪些原始变量导致了样本之间的差异。
优点和缺点
主成分分析方法的主要优点是:
1)仅以方差衡量信息量,不受数据集以外的因素影响;
2)各主成分之间正交,可消除原始数据各变量之间的相互影响;
3)方法简单,易于实现。
主成分分析方法的主要缺点是:
1)各个主成分的含义具有模糊,解释性弱,通常只有信息量而无实际含义;
2)在样本非正态分布时得到的主成分不是最优的,因此特殊情况下方差小的成分也可能含有重要信息。





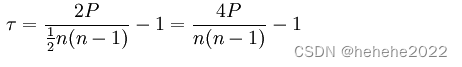




![[2.1.1]进程管理——进程的概念、组成、特征](https://img-blog.csdnimg.cn/img_convert/d8f6ea45cd2a9cfc862038f463152820.png)