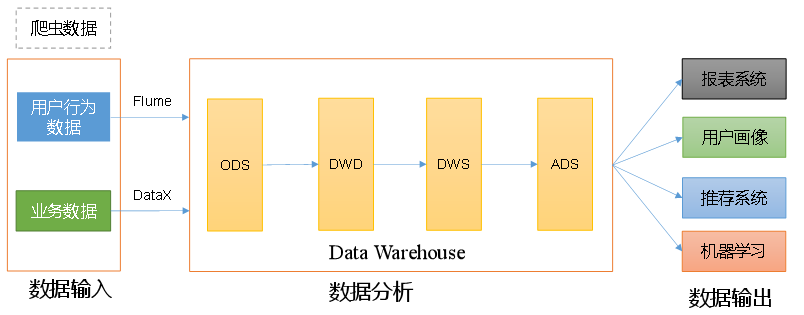
1.3.1 排列与组合

1. 排列

从n个不同元素任取r(r<=n)个元素排成一列(考虑元素出现的先后次序)，称此为一个排列，此种排列的总数为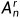=n(n-1)....(n-r+1)=n!/(n-r)！，若r=n,则称为全排列，

2.重复排列

从n个不同元素中每次取出一个,放回后再取出;下一个,如此连续取，次所得的排列称为重复排列，此种重复排列数共有n个，这里， 允许大于么

3.组合

从n个不同元素中任取r(r＜几)个元素并成一组(不考虑元素出现的先后次序），称为一个组合，此种组合的总数为

Ch

n (n

- 1)... (n r+1)

r!

nl

Fr! (n = r)!

易知

A, =Cr!, C, =C

排列组合公式在古典概型的概率计算中经常使用。

1.3.2 古典概型

具有以下两个特点的试验称为古典概型：

(1）有限性：试验的样本空间只含有限个样本点；

(2） 等可能性：试验中每个基本事件发生的可能性相同

对于古典概型，若样本空间中共有n个样本点,事件A 包含人个样本点,则事件

A 的概率为

事件4 中所包含样本点的个数

P(A)

2中所有样本点的个数

容易验证，由上式确定的概率满足公理化定义

【例 1.77（随机取数问题）从1,2,…,10共10个数字中任取一个,取后放回，

先后取出 7个数字,试求下列各事件的概率：

（1） A

=“7 个数字全不相同”；

(2) B

一“不含10与 1”；

（3）C=“10恰好出现两次”。

解随机试验的样本空问共含有10？ 个不同的样本点，则

(3）对于事件C，出现两次 10可以是7次中的任意两次，故有C号种选择，其他5

次中,每次只能取剩下9个数字中的任何一个，故

C3 • 9

p(C)

0.124003.

107

例 1.8】（摸球问题）袋中有a 个白球，6个红球，k个人依次在袋中取一个球，

考虑下列两种取球方式,求第i（i=1，2，

，k）个人取到白球的概率．（1）作放回

抽样(即前一人取一个球观察颜色后放回袋中，后一个人再取一球），（2，作不放回抽

样(即前一人取一个球观察颜色后不放回袋中,后

-个人再取一球)

解记B=“第ii=1,2，

，k)个人取到白球”

1）放回抽样的情况．

第1个人取到白球的概率为-

2+6•因为是放回抽样，所以第2人，第3人，

第k人取到白球的概率均为

a大6，

P(B)=

a th

（2）不放回抽样的情况．

＜个人各取一球，每种取法是一个基本事件，k 个人各取一球共有（a+6（a+6

-1∞[6a+6=（一11=A4,种取法.

当事件 B 发生时，第之人取的应是白球,它可以是a 个白球中的任一个，有a种

取法，其余被取的 k一1个球可以是其余a十6一1个球中的任意k一1个,共有（a+6

=16a+6=②∞16a+6=①=[¢=①+1J>=A千6-1种取法，所以

P(B)

a A"-b-i

A +6

a（a+6-①（a+6=1=1∞（a+6-1

（a +6（a+6=1∞€（a+6一k千17

- (k -1) +1

士6

值得注意的是,P（B)与之无关,即k 个人取球,尽管取球的先后次序不同,每个

人取到白球的概率是一样的,大家机会均等;放回抽样与不放回抽样取到白球的概率

也是一样的

类似的问题如购买彩票等,无论先买后买，中奖的概率是一样的.

【例1.9】（分房问题）

有几个人,每个人都以同样的概率被分配在 N(n≤N)间

房中的每一问中,试求下列各事件的概率：

(① A

一“某指定九间房中各有一人”

(2）B一“恰有几间房,其中各有一人”；

到达,所以由等可能性知这是一个几何概型问题，

样本空间2=1(z,3):0≤z,3≤60)

事件 A=“甲乙能会面”={(z,>)E2:1z一31≤20),因此

pPeA)一 附面餐

< 602

- 402

602

【例 1.11】<蒲丰投针问题）

平面上面有间隔为d (d二0的等距平行线，向平

面任意投掷一枚长为（(L＜d）的针，求针与任一平行线相交的概率.

解以，表示针的中点与最近一条平行线的距离，又以9表示针与直线间的交

角，如图1.2 所示.易知样本空间 2满足

0≤¢

Fd

0

<0<%.

2

由这两式可以确定平面上的一个矩化口，口的面积y”

A二“针与平行线相交” 发生当且仅当0≤五≤元

因此

7

sinode

2

A 的面积

P(A)

一2的面积

2l

di

du

2

+47 (11477-15,5138)

-sing

o

图 1.2蒲丰投针问题

蒲丰投针试验的应用及意义：根据频率的稳定性，当投针试验次数n很大时，测

出针与平行线相交的次数m，则频率值〞

“即可作为PCA)的近似值代人上式,那么

m一dr

n

2nl

dm

利用上式可以计算圆周率元 的近似值.

【例1.12】 随机向边长为1的正方形内投点，试求点投在正方形的一条对角线

上的概率，如图1.3所示．

解样本空间 2=1(z，）:0二z，y＜1),事件 A=

“点投在正方形的对角线上”={(z，»）：2三〉),因此

对角线的面积

O

P(A)

=

=0.

中方形的面积

1

说明：根据前面概率的性质 1,我们知道不可能事件

的概率为 0.本例表明，概率为。的事件未必是不可能事

件,可能发生．类似地，概率为1的事件也未必是必然