专栏：神经网络复现目录

本章介绍的是现代神经网络的结构和复现，包括深度卷积神经网络（AlexNet），VGG，NiN，GoogleNet，残差网络（ResNet），稠密连接网络（DenseNet）。
文章部分文字和代码来自《动手学深度学习》

文章目录

深度卷积神经网络（AlexNet）
- 学习表征
- AlexNet 架构
- 模型设计
- 使用模型进行Fashion-MNIST分类
- - 数据集
  - 超参数、优化器，损失函数
  - 训练
  - 测试
  - 结果

深度卷积神经网络（AlexNet）

学习表征

学习表征（Representation Learning）是机器学习中一个重要的研究领域，旨在通过学习数据的表征，从而更好地完成各种任务。在传统机器学习中，通常需要手工设计特征，然后将这些特征输入到模型中进行训练。这种方法需要具有专业领域知识的人员手工设计特征，费时费力，且很难设计出完美的特征。

而学习表征则是通过机器自动学习数据的特征表示，省去了手动设计特征的过程，提高了效率和性能。学习表征的方法可以分为无监督学习和监督学习两种。其中，无监督学习是指在没有标注信息的情况下学习数据的表征，比如自编码器、受限玻尔兹曼机、深度信念网络等；监督学习则是利用带有标注信息的数据进行学习，比如卷积神经网络、递归神经网络等。

通过学习表征，可以更好地完成各种任务，如图像分类、目标检测、语音识别等。同时，学习表征也是深度学习领域的一个重要研究方向，有助于深入理解深度神经网络的工作原理和特性。

有趣的是，在网络的最底层，模型学习到了一些类似于传统滤波器的特征抽取器。下图从AlexNet论文 (Krizhevsky et al., 2012)复制的，描述了底层图像特征。
在这里插入图片描述
AlexNet的更高层建立在这些底层表示的基础上，以表示更大的特征，如眼睛、鼻子、草叶等等。而更高的层可以检测整个物体，如人、飞机、狗或飞盘。最终的隐藏神经元可以学习图像的综合表示，从而使属于不同类别的数据易于区分。尽管一直有一群执着的研究者不断钻研，试图学习视觉数据的逐级表征，然而很长一段时间里这些尝试都未有突破。深度卷积神经网络的突破出现在2012年。突破可归因于两个关键因素。

AlexNet 架构

若图像大小为A $\times$ A，卷积核大小为D $\times$ D，扩充边缘padding=B，步长stride=C
则卷积后的特征图FeatureMap大小为（A-D+B*2+C）/ C

值得注意的一点：原图输入224 × 224，实际上进行了随机裁剪，实际大小为227 × 227。
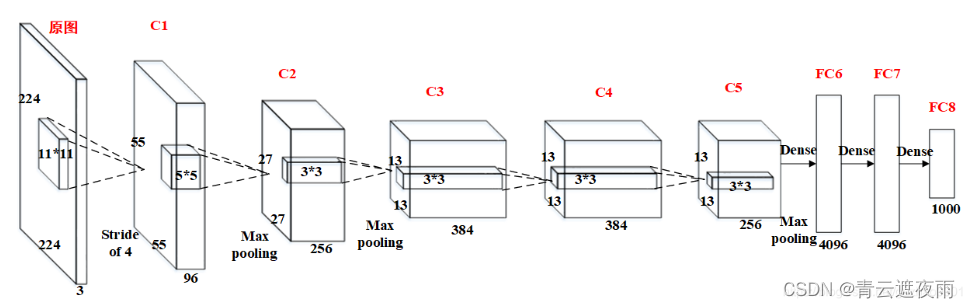
在这里插入图片描述

卷积层C1
C1的基本结构为：卷积–>ReLU–>池化
卷积：输入227 × 227 × 3，96个11×11×3的卷积核，不扩充边缘padding = 0，步长stride = 4，因此其FeatureMap大小为(227-11+0×2+4)/4 = 55，即55×55×96;
激活函数：ReLU；
池化：池化核大小3 × 3，不扩充边缘padding = 0，步长stride = 2，因此其FeatureMap输出大小为(55-3+0×2+2)/2=27, 即C1输出为27×27×96（此处未将输出分到两个GPU中，若按照论文将分成两组，每组为27×27×48）
卷积层C2
C2的基本结构为：卷积–>ReLU–>池化
卷积：输入27×27×96，256个5×5×96的卷积核，扩充边缘padding = 2，步长stride = 1，因此其FeatureMap大小为(27-5+2×2+1)/1 = 27，即27×27×256;
激活函数：ReLU；
池化：池化核大小3 × 3，不扩充边缘padding = 0，步长stride = 2，因此其FeatureMap输出大小为(27-3+0+2)/2=13, 即C2输出为13×13×256（此处未将输出分到两个GPU中，若按照论文将分成两组，每组为13×13×128）；
卷积层C3
C3的基本结构为：卷积–>ReLU。注意一点：此层没有进行MaxPooling操作。
卷积：输入13×13×256，384个3×3×256的卷积核，扩充边缘padding = 1，步长stride = 1，因此其FeatureMap大小为(13-3+1×2+1)/1 = 13，即13×13×384;
激活函数：ReLU，即C3输出为13×13×384（此处未将输出分到两个GPU中，若按照论文将分成两组，每组为13×13×192）
卷积层C4
C4的基本结构为：卷积–>ReLU。注意一点：此层也没有进行MaxPooling操作。
卷积：输入13×13×384，384个3×3×384的卷积核，扩充边缘padding = 1，步长stride = 1，因此其FeatureMap大小为(13-3+1×2+1)/1 = 13，即13×13×384;
激活函数：ReLU，即C4输出为13×13×384（此处未将输出分到两个GPU中，若按照论文将分成两组，每组为13×13×192）；
卷积层C5
C5的基本结构为：卷积–>ReLU–>池化
卷积：输入13×13×384，256个3×3×384的卷积核，扩充边缘padding = 1，步长stride = 1，因此其FeatureMap大小为(13-3+1×2+1)/1 = 13，即13×13×256;
激活函数：ReLU；
池化：池化核大小3 × 3，扩充边缘padding = 0，步长stride = 2，因此其FeatureMap输出大小为(13-3+0×2+2)/2=6, 即C5输出为6×6×256（此处未将输出分到两个GPU中，若按照论文将分成两组，每组为6×6×128）；
全连接层FC6
FC6的基本结构为：全连接–>>ReLU–>Dropout
全连接：此层的全连接实际上是通过卷积进行的，输入6×6×256，4096个6×6×256的卷积核，扩充边缘padding = 0, 步长stride = 1, 因此其FeatureMap大小为(6-6+0×2+1)/1 = 1，即1×1×4096;
激活函数：ReLU；
Dropout：全连接层中去掉了一些神经节点，达到防止过拟合，FC6输出为1×1×4096；
全连接层FC7
FC7的基本结构为：全连接–>>ReLU–>Dropout
全连接：此层的全连接，输入1×1×4096;
激活函数：ReLU；
Dropout：全连接层中去掉了一些神经节点，达到防止过拟合，FC7输出为1×1×4096；
全连接层FC8
FC8的基本结构为：全连接–>>softmax
全连接：此层的全连接，输入1×1×4096;
softmax：softmax为1000，FC8输出为1×1×1000；

模型设计

class AlexNet(nn.Module):
    def __init__(self):
        super(AlexNet,self).__init__()
        #卷积层
        self.conv = nn.Sequential(
            #C1
            nn.Conv2d(in_channels=1,out_channels=96,kernel_size=11,padding=0,stride=4),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=3,stride=2),
            #C2
            nn.Conv2d(in_channels=96,out_channels=256,kernel_size=5,padding=2,stride=1),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=3,stride=2),
            #C3
            nn.Conv2d(in_channels=256,out_channels=384,kernel_size=3,padding=1,stride=1),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=3,stride=2),
            #C4
            nn.Conv2d(in_channels=384,out_channels=384,kernel_size=3,padding=1,stride=1),
            nn.ReLU(),
            #C5
            nn.Conv2d(in_channels=384,out_channels=256,kernel_size=3,padding=1,stride=1),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=3,stride=2),
            nn.Flatten(),#拉直层
        )
        #全连接层
        self.fc=nn.Sequential(
            #FC6
            nn.Linear(256*5*5,4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            #FC7
            nn.Linear(4096,4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096,10),
        )

    def forward(self,img):
        feature=self.conv(img)
        output=self.fc(feature)
        return output

    def layers(self):
        return [self.conv, self.fc]

使用模型进行Fashion-MNIST分类

数据集

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

超参数、优化器，损失函数

#超参数，优化器和损失函数
batch_size = 128
train_iter, test_iter = load_data_fashion_mnist(batch_size, resize=224)
lr, num_epochs = 0.01, 10
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()

训练


def train(net, train_iter, test_iter, num_epochs, lr, device):
    def init_weights(m):
        if type(m) == nn.Linear or type(m) == nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    net.apply(init_weights)
    print('training on', device)
    net.to(device)
    for epoch in range(num_epochs):
        # 训练损失之和，训练准确率之和，样本数
        net.train()
        train_step = 0
        total_loss = 0.0#总损失
        total_correct = 0#总正确数
        total_examples = 0#总训练数
        for i, (X, y) in enumerate(train_iter):
            optimizer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            optimizer.step()

            total_loss += l.item()
            total_correct += (y_hat.argmax(dim=1) == y).sum().item()
            total_examples += y.size(0)

            train_step+=1
            if(train_step%50==0):#每训练一百组输出一次损失
                print("第{}轮的第{}次训练的loss:{}".format((epoch+1),train_step,l.item()))

                
train(net,train_iter,test_iter,num_epochs,lr,device)

测试

from d2l import torch as d2l
def predict(net, test_iter, n=6):  #@save
    for X, y in test_iter:
        X, y = X.to('cuda'), y.to('cuda')
        break
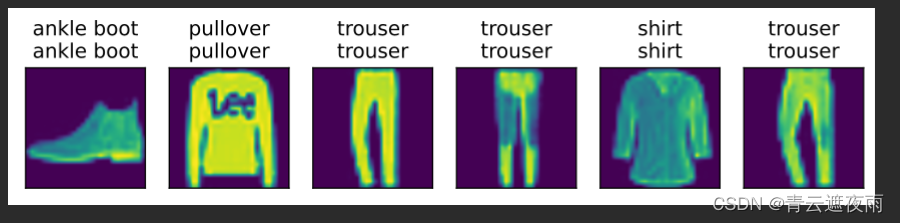
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].cpu().reshape((n, 224, 224)), 1, n, titles=titles[0:n])
predict(net, test_iter)