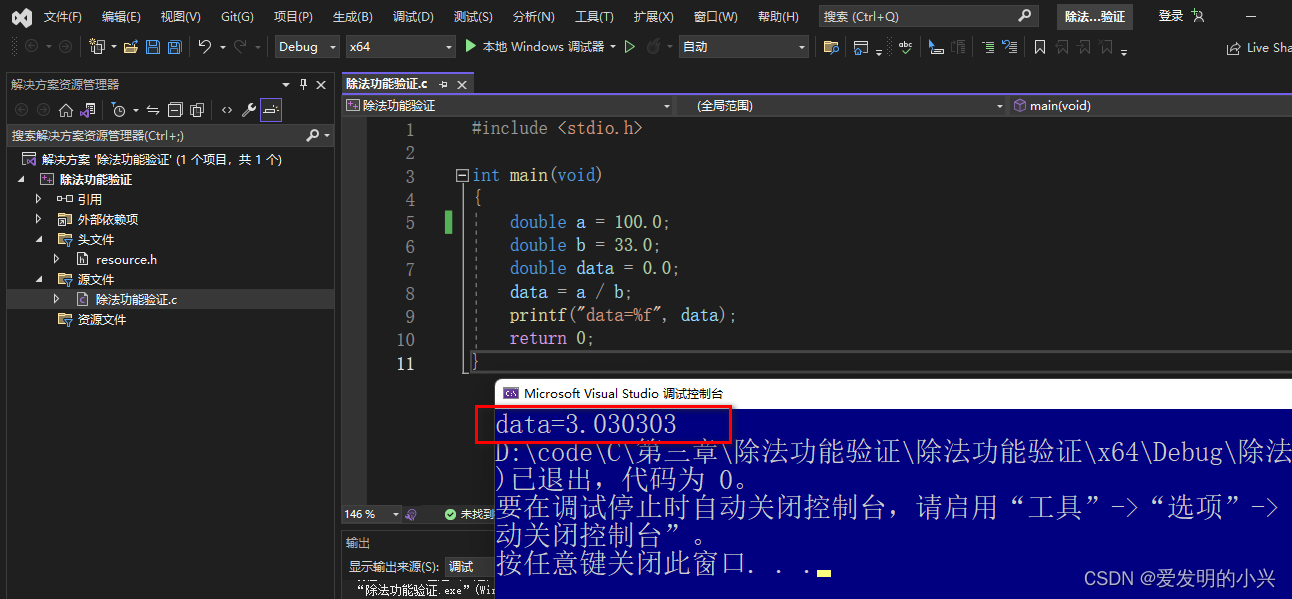
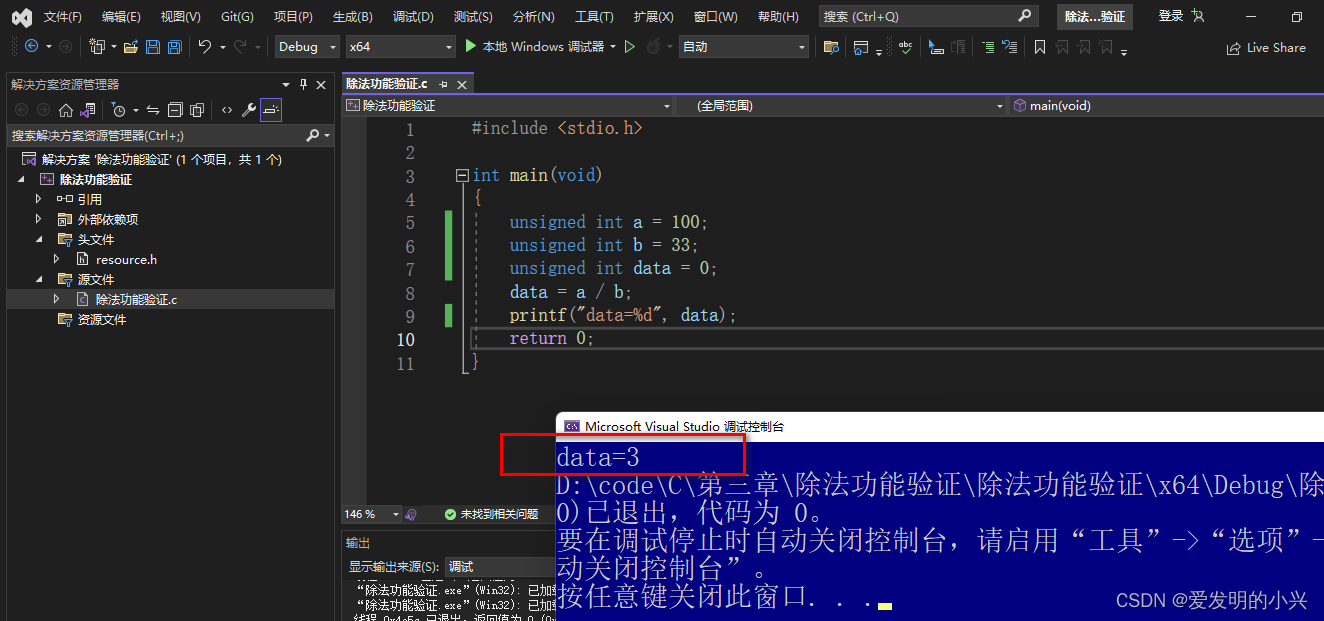
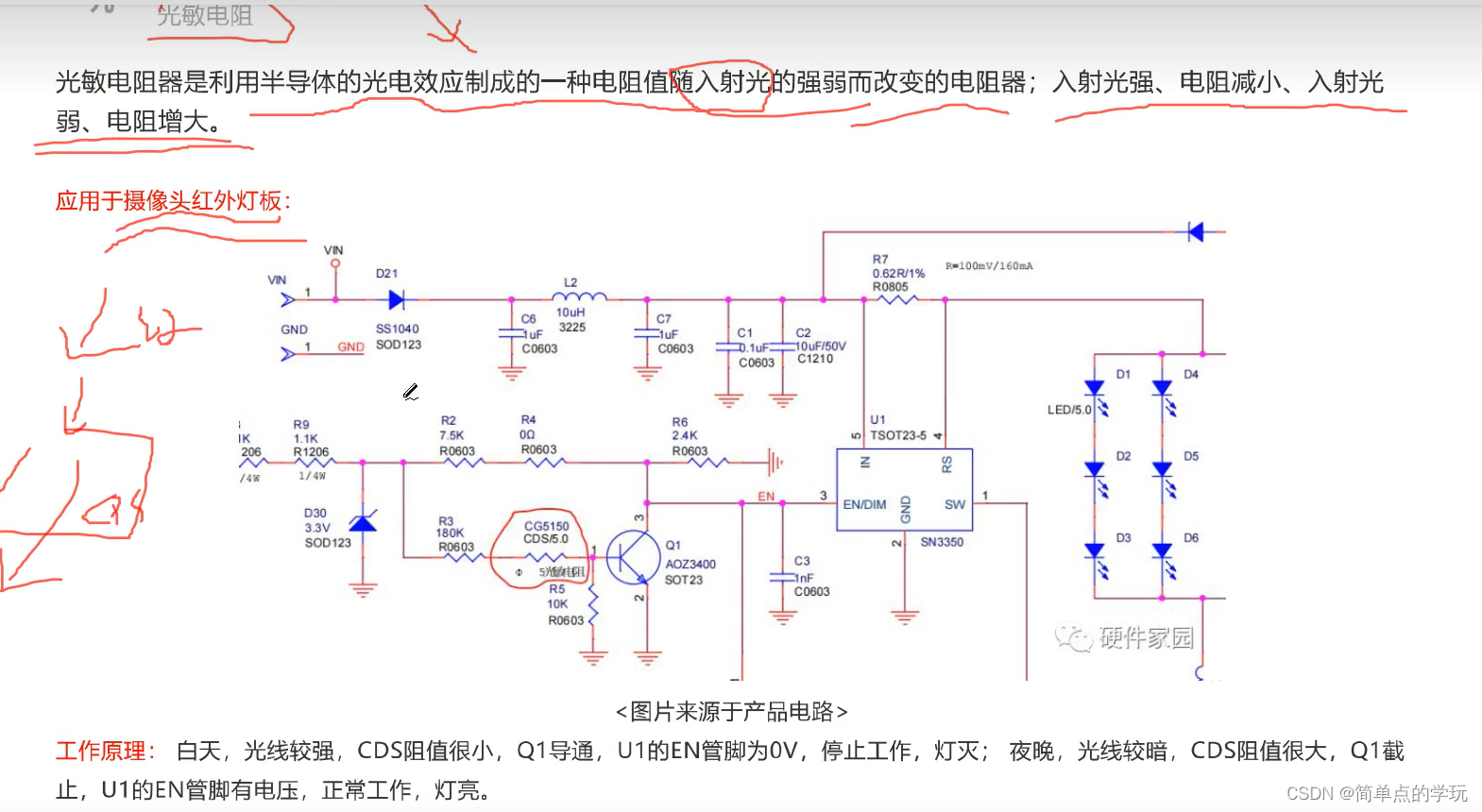
例题3-1 编写一个函数,实现华氏度和摄氏度的转化。
已知公式:c = (5/9)*(f-32)
#include <stdio.h>
double f_value = 0;
double c_value = 0;
int main(void)
{
printf("请输入华氏温度\n");
scanf("%lf",&f_value);
c_value = (5.0/9.0)*(f_value-42);
printf("华氏温度=%0.2f也就是摄氏度温度=%0.2f",f_value,c_value);
return 0;
}
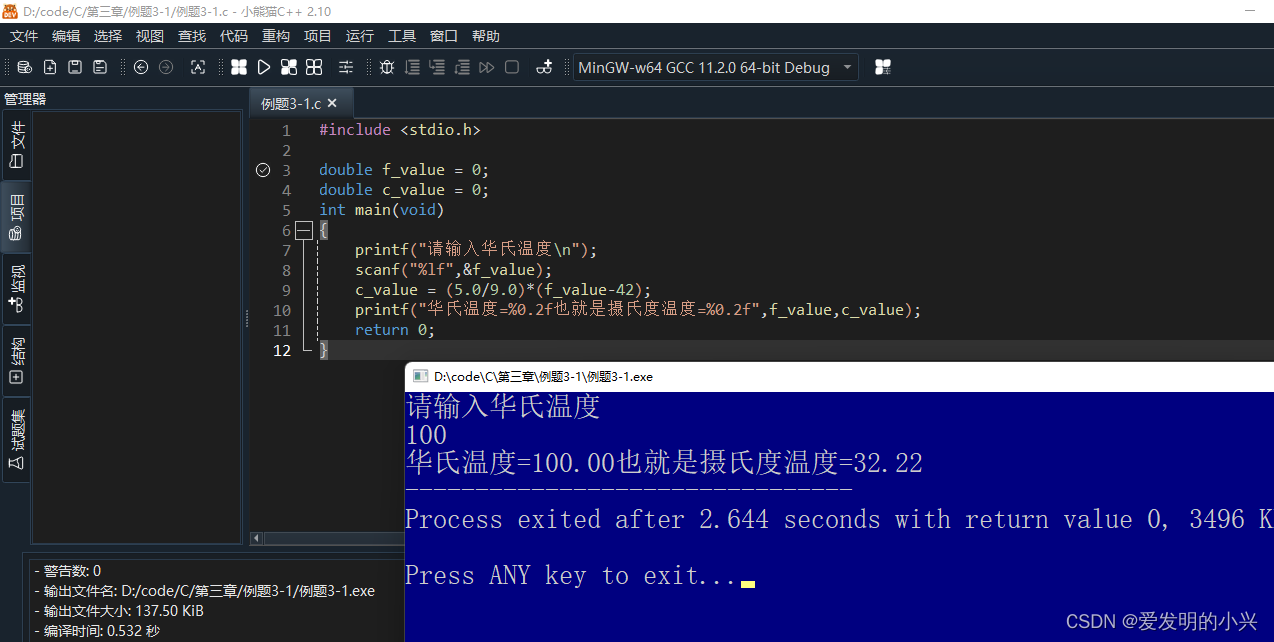
例题3-2 计算存款利息。有1000元。想存一年,有3种方法可选
(1)一年期活期,年利率为r1
(2)一年期定期,年利率为r2
(3)存两次半年定期,年利率为r3
分别计算这三种方式得到的本息和。
#include <stdio.h>
double p0 = 1000,r1 = 0.0036, r2 = 0.0225, r3 = 0.0198;
//p1表示一年活期获得的钱
//p2表示一年定期获得的钱
//p3表示两次半年定期获得的钱
double p1 = 0, p2 = 0, p3 = 0;
int main(void)
{
p1 = p0*(1 + r1);
p2 = p0*(1 + r2);
p3 = p0*(1 + r3/2)*(1 + r3/2);
printf("p1 = %f, p2 = %f, p3 = %f",p1,p2,p3);
return 0;
}
常量主要包括,整型常量、实型常量、字符常量、字符串常量、符号常量。
两个重要点
#define PI 3.1415926 定义符号常量(预编译)
const float pi = 3.1415926; 定义常变量
一个注意点
标识符只能用字母,数字和下画线组成,且第一个字符必须是字母或下画线。
数据类型(常见)
整型(int)、短整型(short int)、长整型(long int)、字符型(char)、布尔型(bool)。
单精度浮点型(float)、双精度浮点型(double)。
枚举型(enum)、空型(void)。
指针类型(*)、数组类型([])、结构体类型(struct)、共用体类型(union)、函数类型。
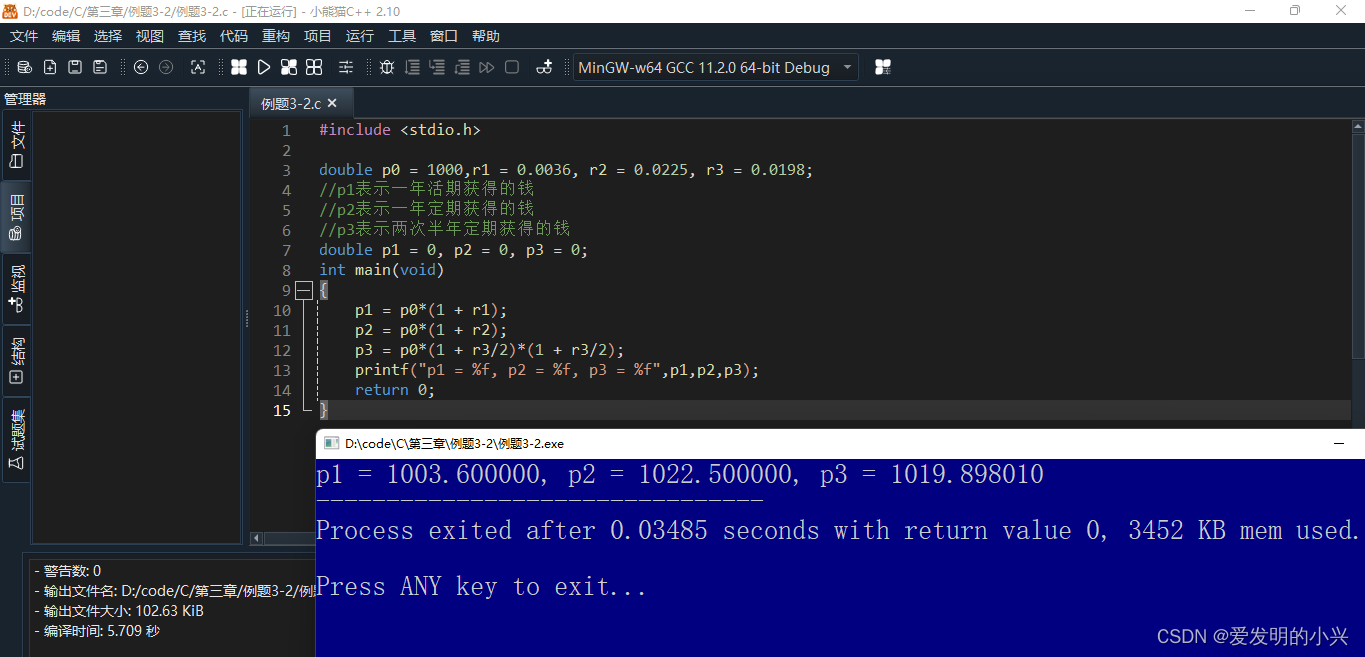
书中的short int类型的取值范围(其他类似计算)
short int占两个字节。示意图如下图所示,也可以理解为16个小格子,每个小格子只能存放0或1。越往左的小盒子是数据二进制形式下的高位,越往右的小盒子是数据二进制形式下的的低位。
对于short int来说,又可以分为符号型和无符号型。其中,在上图中最左边的小盒子(最高位)是表示的符号位。下面来分情况来进行讨论。
首先,对于无符号的short int类型来说,能取得最小值为0,也就是16个小格子全部填0。
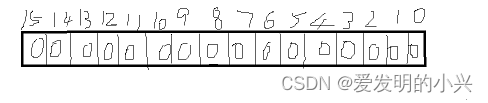
能取得最大值是2^16-1,也即是16个小格子全部填1。所以无符号的short int类型可取的范围是0~65535。

接着,对于有符号的short int类型来说,这时候最高位是符号位。
当最高位,也就是符号位为0的时候,能取得最大值为2^15-1,也即是除了符号位外的15个小格子全部填1。

能取得最小值为0,也即是除了符号位外的15个小格子全部填0。

当最高位,也就是符号位为1的时候,能取得最大值为-1。
这时候需要了解-1的存储形式。
首先写出该数的绝对值,也就是1的二进制形式,0000 0000 0000 0001。
接着需要按位取反,1111 1111 1111 1110。
最后在加1即可以得到-1的存储结构,1111 1111 1111 1111。

能取得最小值-2^15=-32768。这时候需要了解-32768的存储形式。
首先写出该数的绝对值,也就是32768的二进制形式,1000 0000 0000 0000。
接着需要按位取反,0111 1111 1111 1111。
最后在加1即可以得到-32768的存储结构,1000 0000 0000 0000。
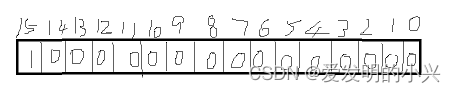
综上所述,我们求得,对于无符号的short int来说,取值范围为0~65535。
对于有符号的short int来说,取值范围为-32768~32767。
浮点型常量常见问题
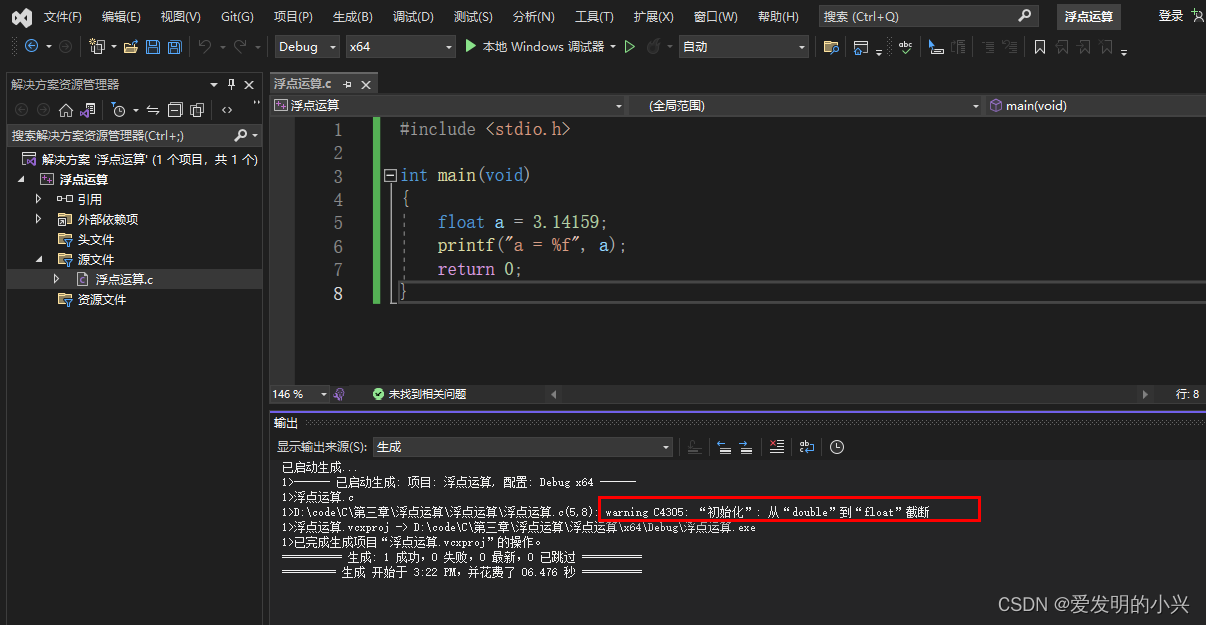
在vs中编译下面的程序,会出现一行警告,这个意思是从double到float进行转化,会损失精度。这是因为3.14159这个数,系统会默认把浮点型变量按照double类型处理,但是最后在赋值中需要赋值给一个float型的a,所以才会出现这样的问题。
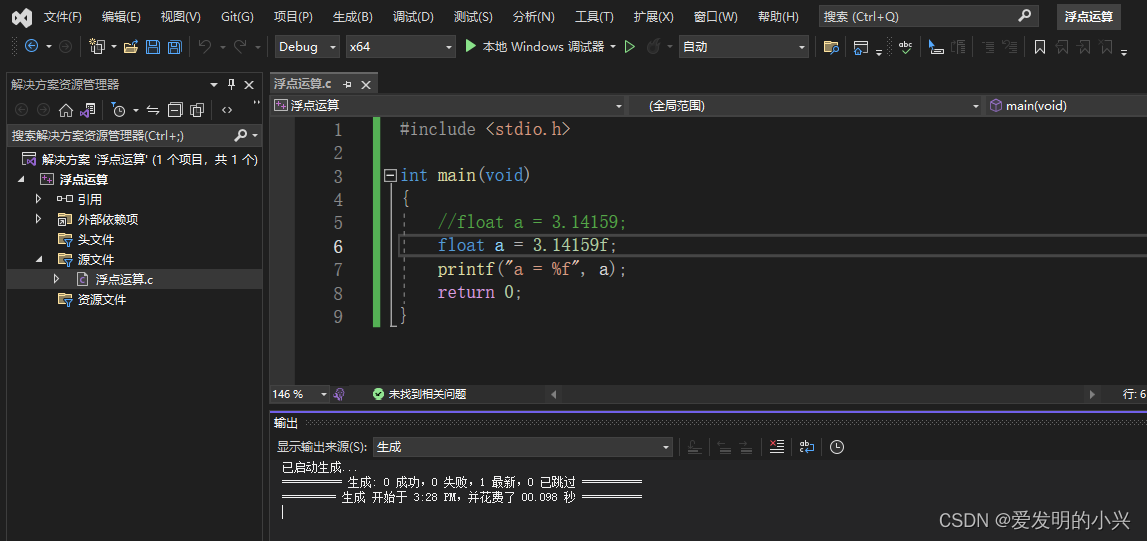
解决办法可以有两种,下图是解决的办法。
算数运算符
+ 加法
- 减法
* 乘法
/ 除法
% 求余
这里重点说一下,对与除法,两个实数相除得到的结果是双精度实数,但是两个整数相除,得到的是整数。