在去年的文章中我们介绍过Bayesian Bootstrap,今天我们来说说Weighted Bayesian Bootstrap
Bayesian bootstrap
贝叶斯自举法(Bayesian bootstrap)是一种统计学方法,用于在缺乏先验知识的情况下对一个参数的分布进行估计。这种方法是基于贝叶斯统计学的思想,它使用贝叶斯公式来计算参数的后验分布。
在传统的非参数自举方法中,样本是从一个已知分布中抽取的,然后使用这些样本来估计这个分布的性质。然而,在实际问题中,我们通常无法获得这样的先验知识,因此需要使用其他方法来估计分布。
贝叶斯自举法是一种替代方法,它不需要先验知识,而是从样本中抽取子样本,然后使用这些子样本来构建一个后验分布。这个后验分布表示了给定这个样本,参数的可能取值。通过在这个分布上采样,可以产生类似于非参数自举的样本,然后可以使用这些样本来估计参数的性质。
与传统的自举方法相比,贝叶斯自举法可以提供更好的参数估计,特别是在样本较小或参数分布复杂的情况下。
Python实现
使用numpy和scipy,我们可以很容易实现Bayesian bootstrap
importnumpyasnp
importscipy.statsasss
classBayesianBootstrap:
def__init__(self, concentration: float=1.):
self.n_draws=100000
self.bins=100
self.concentration=concentration
defsample(self, obs: np.ndarray, weights: np.ndarray=None):
# If no weights passed, use uniform Dirichlet
ifweightsisNone:
weights=np.ones(len(obs))
# Normalize weights to mean concentration
weights=weights/weights.mean() *self.concentration
# Sample posteriors
draws=ss.dirichlet(weights).rvs(self.n_draws)
means= (draws*obs).sum(axis=1)
vars=draws* (obs-means.reshape(self.n_draws, 1)) **2
returnmeans, np.sqrt(vars.sum(axis=1))
defdistribution(self, obs: np.ndarray, weights: np.ndarray=None):
# Sample and create distribution objects
means, stds=self.sample(obs, weights)
hist_mean=np.histogram(means, bins=self.bins)
hist_std=np.histogram(stds, bins=self.bins)
returnss.rv_histogram(hist_mean), ss.rv_histogram(hist_std)
.sample()方法是这里的核心,该方法计算来自观察的后验样本的平均值和标准偏差。与经典的自举法相比即使对于非常大量的样本,因为使用了向量化的计算,所以不必担心速度问题。distribution()函数是从样本直方图中返回scipy分布对象,这样我们可以使用标准的API来计算任何后验统计信息。
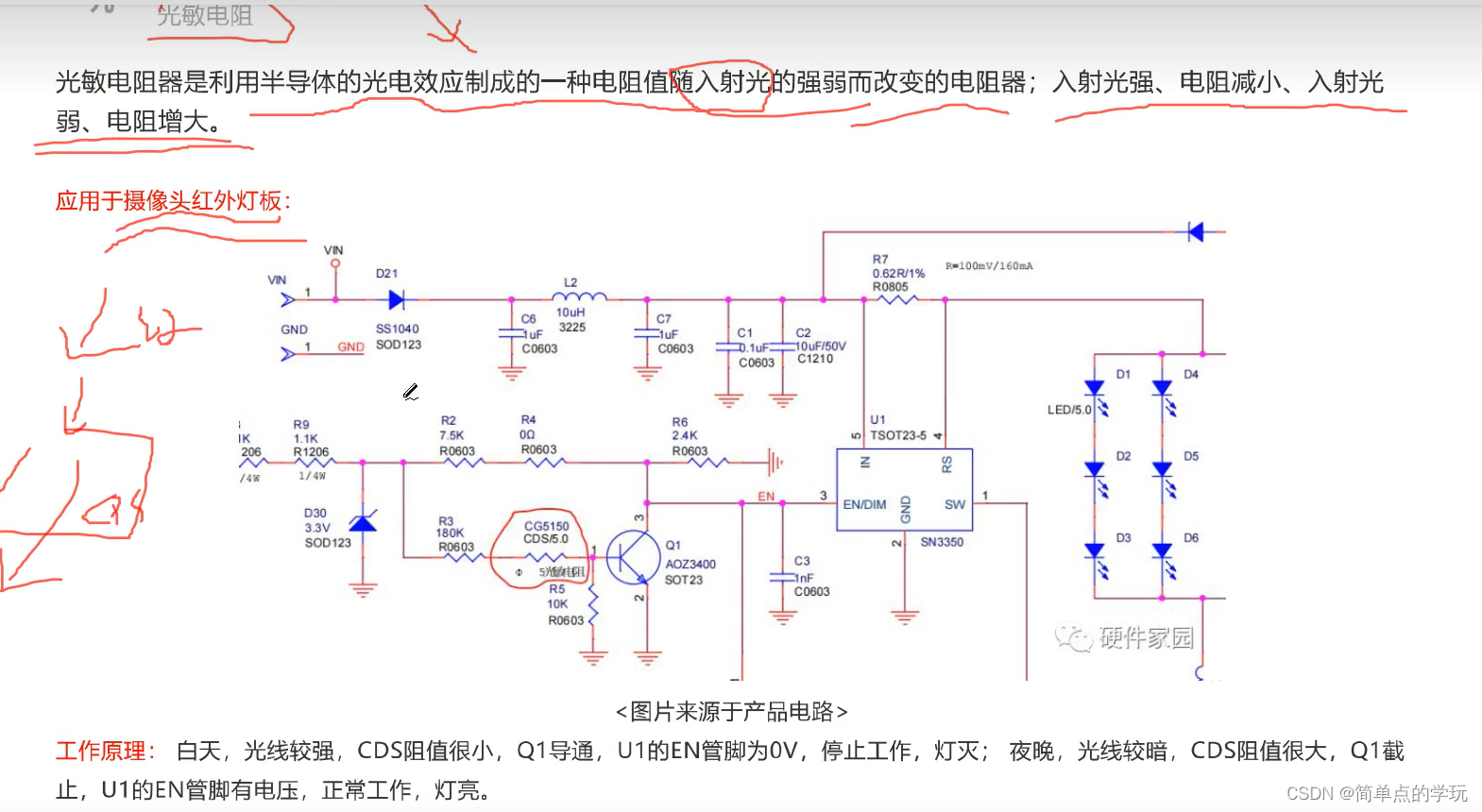
我们从正态分布中抽取一些样本obs = ss.norm(0.1, 0.02).rvs(8),查看贝叶斯自举法是如何执行的。如下图所示,即使对于这个微型样本,后验也是平滑的,并且包含了均值和标准差的真实值。
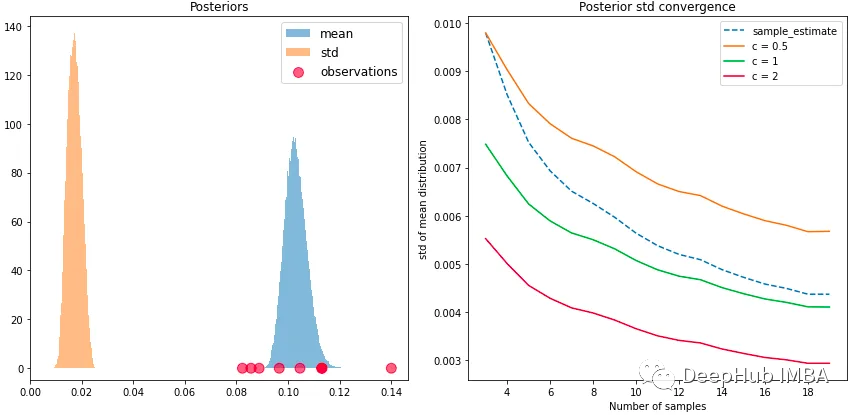
左:平均值和标准差的贝叶斯自举后验。右:不同集中度的平均值标准偏差的收敛。
集中度(Concentration)
我们一直说贝叶斯自举是非参数的,但是这里又出现了一个集中度参数,这是什么呢?事实上,这一点经常被忽略,当我们的分布超越均匀狄利克雷分布时,它对加权很重要,也就是说我们的分布不是由一组均匀的值参数化的。
并非所有的均匀数组都是相等的,而是他们的规模很重要。这就是集中度所控制的。即使狄利克雷样本总是加起来等于1,但标准差随着集中度的增加而增加。也就是说低集中度意味着样本值非常均匀,而更高的集中度则将更多的权重分配给少数样本值,从而降低后验分布的方差。那么问题就来了,应该使用什么值来进行无偏参数不确定性估计呢?
一般情况下我们都是默认使用1,但在以前论文中也没有明确的共识。但是对我们手头的问题,可以找到一个明显的基准。假设我们想要估计样本的平均值。那么已知平均数的标准差大约为σ / N^(1/2),其中σ是无偏样本标准差,N是样本数。
上图(右)显示了不同集中度的标准差作为样本数量的函数的平均值。无偏样本估计在集中度=0.5和1之间平滑插值,随着N的增加收敛于后者。虽然这并不一定正确,但是由于我们没有先验理由来更加自信或不自信地估计,所以使用此默认值似乎是合理的。但是在少数样本情况下,贝叶斯自举法可能对均值过度自信。
分布估计
继续回到非参数估计,后验分布告诉我们,数据来自这种分布(其均值和标准差以这种方式分布的)。要实际建模基础分布本身,需要进行建模选择,比如需要假设数据来自正态分布。scipy提供了一种基于最大似然估计将分布拟合到样本中的快速方法ss.norm.fit(obs)。对于正态分布,只需要样本均值和标准差作为参数。
但是由于我们的贝叶斯自举法参数估计也是分布,所以估计的不仅仅是一个单独的分布,而是一个分布族,如下图所示,每个可能的分布都是通过对均值和标准差后验进行采样得到的。随着样本数量的增加,分布族越来越接近真实分布。
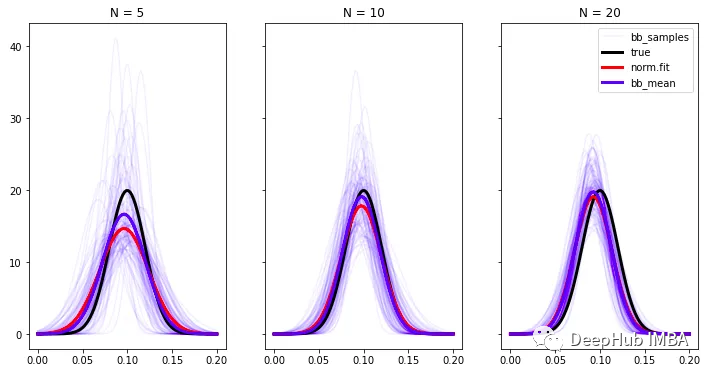
基本分布估计与样本数N的收敛性
加权
贝叶斯自举法通过将非均匀值的向量传递给狄利克雷分布来实现加权,每个值表示每个观测值的相对权重。为了防止主导值偏向抽样,需要将它们归一化到所需的平均集中度。
为了说明这一点,我们使加权的重要性更加透明,使用了具有显著刻度差异的固定数量的试验:
rate_true=0.05
trials=np.array([50, 100, 200, 500, 800, 1000, 1500])
success=ss.binom.rvs(trials, rate_true)
obs=success/trials
可以看到由于试验次数少而方差大,观察到的比率的平均值通常偏离真实比率,我们可以通过将每个观测值的试验次数作为权重来考虑方差的异质性。如下图所示,观测标记的大小反映了权重,加权估计比无权重估计更接近真实率,并且具有更高的置信度。
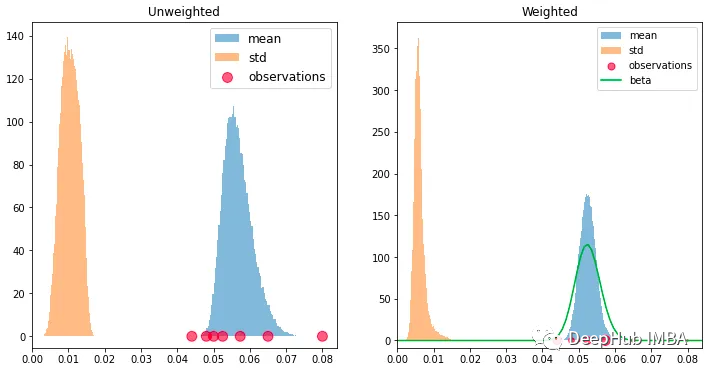
左:未加权估计。右:试验加权估计。
我们将试验成功配对样本视为 beta 随机变量,我们还可以在左图中绘制总 beta 分布,计算方式为将观测值相加:
x=np.linspace(0, 0.1, 100)
a=success.sum()
b=trials.sum() -a
beta_pdf=ss.beta(a, b).pdf(x)
这也提供了同样好的平均值估计。这种方法中的权重是隐式的,因为求和会自动地给较少数量的试验较少的权重。
上面我们可以看到:权重确实是有用的。但是如果成功率随时间变化呢?我们可能无法知道当前的真实值,但可以对最近的观测值赋予更大的权重。
为了让情况变得更加复杂,我们假设成功率随时间变化,试验次数也随之变化。例如,产品的季节性效应即需求突然增加并导致更高的转化率:
rates_true=np.linspace(0.05, 0.1, size)
trials_mean=np.linspace(1000, 1200, size)
trials=ss.norm(trials_mean, 200).rvs(10).astype(int)
success=ss.binom.rvs(trials, rates_true)
obs=success/trials
time_weights=np.log2(np.linspace(1.1, 2, size))
weights=trials*time_weights
如何分配时间加权依赖于领域知识和建模选择。为了说明加权,我们选择对数加权,因为它赋予最近的观察更多的权重,然后迅速衰减。我们还像上面一样包括了试验加权。将它们传递给贝叶斯自举法显然会给出更好的(尽管不完美)的估计,当前真实的转化率已经从0.05上升到了0.10,如下图所示。
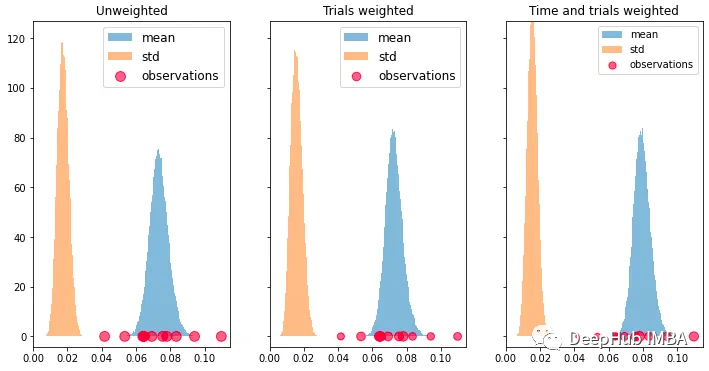
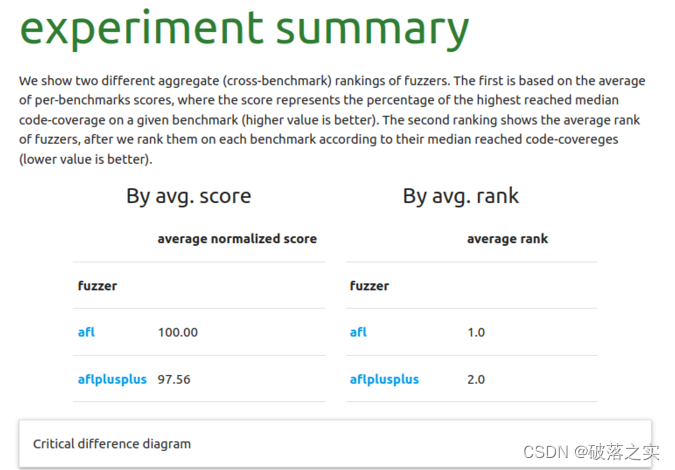
总结
加权贝叶斯自举法是贝叶斯自举法的一种变体,其中观测值被赋予权重,反映它们在样本中的相对重要性。权重用于从后验分布中进行抽样,具有较高权重的观测值被抽样更频繁。当数据存在异质性,可能会影响感兴趣的估计量时,例如某些观测值具有较大的方差或比其他观测值更近期时,这种方法尤其有用。
加权贝叶斯自举法可以以类似于标准贝叶斯自举法的方式实现,但权重应纳入到狄利克雷分布中。狄利克雷分布的集中度参数可以设置为归一化为一的权重。然后从贝叶斯自举法中获得的加权后验分布可以用于估计感兴趣的数量,例如平均值、中位数或方差。
在加权贝叶斯自举法中,权重可以根据具体问题的不同标准进行分配。例如,如果数据来自不同可靠性的来源,则可以分配反映每个来源可靠性的权重。如果数据是随时间收集的,且存在时间趋势,则可以将更高的权重分配给更近期的观测值(我们例子中的log)。
加权贝叶斯自举法是处理数据异质性和时间趋势的强大工具,并且可以提供比标准贝叶斯自举法更准确和精确的估计。贝叶斯自举法的灵活性来自于其使用狄利克雷先验,这使得它可以适应数据中不同的不确定性水平,并通过加权考虑时间变化。在不要求任何定量严谨性的情况下,如果:
- 只有很少的数据
- 关心的是估计的不确定性
- 要尽可能地保持公正
贝叶斯自举法是一种有用的工具。但是如果有大量数据,则使用样本统计量就足够了,那就不用费事了。
https://avoid.overfit.cn/post/8bffb6de8f6b470d9399fd54be44bb97