如题,这是一篇深度学习相关数学原理总结文,由于深度学习中涉及到较多的概率论知识(包括随机过程,信息论,概率与统计啥啥啥的),而笔者概率知识储备属实不行,因此特意开一章来总结(大部分是概率相关)。
文章目录
- 概率分布
- 离散型随机变量
- 连续性随机变量
- 均匀分布
- 条件概率
- 贝叶斯公式
- 链式法则
- 经验分布
- 置信域
- 极大似然估计
- KL散度
- 熵
- KL散度(相对熵)
- 交叉熵
- 拓展:条件熵
- 高斯分布(正态分布)
- 马尔可夫链
- 数学定义
- 转移概率矩阵
- 状态转移矩阵(转移概率矩阵)的稳定性
- 状态的区分(Classification of states)
- 蒙特卡洛方法
- 蒙特卡罗方法的应用
- 蒙特卡罗方法求定积分
- 随机投点法
- 平均值法(期望法)
- 蒙特卡罗采样方法
- 常见的概率分布采样
- 接受拒绝采样(取舍采样)
- 马尔可夫链蒙塔卡罗采样(MCMC)
- Metropolis算法
- Metropolis-Hastings 采样算法
- 总结
概率分布
首先需要理解的概念是随机变量(random variable),顾名思义,它就是某一变量可能随机的取不同数值。随机变量可以是离散的也可以是连续的。
概率分布就是对随机变量取不同数值的可能性的一种描述。
离散型随机变量
离散型随机变量,我们用概率质量函数(probability mass function,简称PMF)来描述,或者也可以称它为分布律或者概率分布,它是对随机变量的状态到随机变量取这种状态的概率的一种映射。变量x取变量值为x的PMF常用P(x=x)表示,PMF也可以用来描述多个变量,又叫做联合概率分布(joint probability distribution),比如P(x=x,y=y)代表了变量x取值x同时变量y取值y的概率。
例如硬币抛出正面的事件为
x
1
x_1
x1,反面为
x
2
x_2
x2,其概率为
P
(
X
∣
x
1
)
=
1
2
P(X|x_1)=\frac {1}{2}
P(X∣x1)=21
分布律为:
| X | x 1 x_1 x1 | x 2 x_2 x2 |
|---|---|---|
| p i p_i pi | 1 2 \frac{1}{2} 21 | 1 2 \frac{1}{2} 21 |
函数P作为变量x的PMF必须满足以下条件:
- P的域包含x的所有可能状态,也就是说比如一个骰子的分布律应该是每个数字都是1/6,如果仅有数字1~5的概率不能称为PMF,因为分布律必须包含所有可能情况
- ∀ x ∈ X , 0 ≤ P ( x ) ≤ 1 \forall x \in X,0 \leq P(x) \leq 1 ∀x∈X,0≤P(x)≤1。因为任意概率事件发生的概率都不能为负数,也不能大于1
- ∑ x ∈ X P ( x ) = 1 \sum_{x\in X}P(x)=1 ∑x∈XP(x)=1,归一化条件,所有事件的概率之和一定为1
连续性随机变量
对于连续变量,我们用概率密度函数(probablity density function,简称PDF)来描述,常用p(x)来表示。对于连续变量,p(x)不再直接代表x取某一值的概率,而是指在这一值的极微小区间的积分 p ( x ) d x p(x)dx p(x)dx
如X落在(a,b]区间的概率为:
P
(
a
<
X
≤
b
)
=
P
(
X
≤
b
)
−
P
(
≤
a
)
=
F
(
b
)
−
F
(
a
)
=
∫
a
b
f
(
x
)
d
x
P(a < X \le b)=P(X \le b)-P(\le a)=F(b)-F(a)=\int ^b_a f(x)dx
P(a<X≤b)=P(X≤b)−P(≤a)=F(b)−F(a)=∫abf(x)dx
在
f
(
x
)
f(x)
f(x)的连续点处有
F
′
(
x
)
=
f
(
x
)
F'(x)=f(x)
F′(x)=f(x)
PDF同样必须满足以下条件:
- P的域包含x的所有可能状态
- ∀ x ∈ X , P ( x ) ≥ 0 \forall x \in X,P(x) \geq 0 ∀x∈X,P(x)≥0。注意这里只要求p(x)不小于零,而p(x)是可以大于1的。
- ∫ P ( x ) d x = 1 \int P(x)dx=1 ∫P(x)dx=1
均匀分布
像刚才举得骰子的例子,如果样本空间X是一个有限集,而且每种试验结果等概率出现,那么我们称X服从均匀分布
当其为离散型随机变量的分布律: P ( X = x i ) = 1 n P(X=x_i)=\frac{1}{n} P(X=xi)=n1
当其为连续性随机变量的概率密度函数: f ( x ) = { 1 b − a , a<x<b 0 , else f(x)=\begin{cases} \frac{1}{b-a} ,\space\text{a<x<b} \\ 0 ,\text{else} \end{cases} f(x)={b−a1, a<x<b0,else
条件概率
条件概率(conditional probability)研究的是在某一事件发生的前提下,另一个事件发生的概率。我们用
P
(
x
∣
y
)
P(x|y)
P(x∣y)来表示在事件y发生的前提下事件x发生的概率,可用如下公式计算:
P
(
x
∣
y
)
=
P
(
x
,
y
)
P
(
y
)
P(x|y)=\frac {P(x,y)}{P(y)}
P(x∣y)=P(y)P(x,y)
其中
P
(
x
,
y
)
P(x,y)
P(x,y)指的是事件x,y都发生的概率,也可以写作
P
(
x
y
)
P(xy)
P(xy)
贝叶斯公式
P ( x ∣ y ) = P ( y ∣ x ) P ( x ) P ( y ) P(x|y)=\frac {P(y|x)P(x)}{P(y)} P(x∣y)=P(y)P(y∣x)P(x)
链式法则
如果事件之间相互独立(即事件的发生相互都不影响),则可以使用链式法则计算
P
(
a
,
b
.
.
.
n
)
=
P
(
a
)
P
(
b
)
.
.
.
P
(
n
)
P(a,b...n)=P(a)P(b)...P(n)
P(a,b...n)=P(a)P(b)...P(n)
推广到n个事件则有
P
(
X
1
,
X
2
,
.
.
.
X
n
)
=
P
(
X
1
∣
X
2
,
X
3...
X
n
)
∗
P
(
X
2
∣
X
3
,
X
4...
X
n
)
.
.
.
P
(
X
n
−
1
∣
X
n
)
∗
P
(
X
n
)
P(X1, X2, ... Xn) = P(X1 | X2, X3 ... Xn) * P(X2 | X3, X4 ... Xn) ... P(Xn-1 | Xn) * P(Xn)
P(X1,X2,...Xn)=P(X1∣X2,X3...Xn)∗P(X2∣X3,X4...Xn)...P(Xn−1∣Xn)∗P(Xn)
经验分布
如果我们想知道某个随机变量X的分布F,这在一般情况下当然是无法准确知道的,但如果我们手上有它的一些独立同分布的样本,可不可以利用这些样本?一个很简单的办法就是,把这些样本的“频率”近似为随机变量的“概率”
经验分布函数(empirical distribution function):给每个点
1
n
\frac {1}{n}
n1的概率质量(大概类似n个样本的均匀分布?),得到CDF:
F ^ n ( x ) = ∑ i = 1 n I ( X i ≤ x ) n \hat F_n(x)=\frac {\sum ^n_{i=1} I(X_i \leq \space x) }{n} F^n(x)=n∑i=1nI(Xi≤ x)
- 期望 E ( F ^ n ( x ) ) = F ( x ) \Bbb E(\hat F_n(x))=F(x) E(F^n(x))=F(x)
- 方差 ( V 或 δ ) (V或δ) (V或δ), V ( F ^ n ( x ) ) = F ( x ) ( 1 − F ( x ) ) n V(\hat F_n(x))=\frac {F(x)(1-F(x))}{n} V(F^n(x))=nF(x)(1−F(x))
- 均方误差(各数据偏离真实值差值的平方和的平均数) M S E = F ( x ) ( 1 − F ( x ) ) n MSE=\frac {F(x)(1-F(x))}{n} MSE=nF(x)(1−F(x))
- F ^ n ( x ) → p F ( x ) \hat F_n(x) \overset{p}{\to} F(x) F^n(x)→pF(x),经验分布函数依概率收敛于总体的分布函数
置信域
置信域策略优化 TRPO
置信域是一种限制参数搜索的方法,它限制了搜索空间,使算法更加稳定。
在几何上,我们可以把置信域直观地表示为一个圆形,它的圆心是搜索空间中的某一点,而半径决定了搜索空间的范围。

极大似然估计
生成模型(2)-极大似然法
极大似然估计是对概率模型参数进行估计的一种方法,例如有一个包含N个样本的数据集
{
x
(
1
)
,
x
(
2
)
,
.
.
.
,
x
(
N
)
}
\lbrace x^{(1)} , x^{(2)},... , x^{(N)} \rbrace
{x(1),x(2),...,x(N)},数据集中每个样本都是从某个未知的概率分布
p
d
a
t
a
(
x
)
p_{data}(x)
pdata(x)中独立采样获得的,若我们已经知道
p
θ
(
x
)
p_θ(x)
pθ(x)的形式,但是
p
θ
(
x
)
p_θ(x)
pθ(x)的表达式里仍包含未知参数θ,那问题就变成了:如何使用数据集来估算
p
θ
(
x
)
p_θ(x)
pθ(x)中的未知参数θ?例如
p
θ
(
x
)
p_θ(x)
pθ(x)是一个均值和方差参数还未确定的正态分布,那么如何用样本估计均值和方差的准确数值?
在极大似然法中,首先使用所有样本计算似然函数 L ( θ ) L(θ) L(θ):
L ( θ ∣ x ) = ∏ i = 1 N P θ ( X = x i ∣ θ ) L(θ|x)=\displaystyle\prod^{N}_{i=1} P_θ(X=x^{i}|θ) L(θ∣x)=i=1∏NPθ(X=xi∣θ),这是如何得到的?(此处的θ并不代表事件,而是参数,也可写作 P θ ( X = x i ; θ ) P_θ(X=x^{i};θ) Pθ(X=xi;θ))
首先似然函数
L
(
θ
∣
x
)
=
P
θ
(
X
=
x
∣
θ
)
,
L(θ|x)=P_θ(X=x|θ),
L(θ∣x)=Pθ(X=x∣θ),其中由于
P
(
x
i
)
P(x^i)
P(xi)是独立事件,因此
P
(
X
=
x
∣
θ
)
=
P
(
x
1
∣
θ
)
P
(
x
2
∣
θ
)
.
.
.
P
(
x
n
∣
θ
)
P(X=x|θ)=P(x^1|θ)P(x^2|θ)...P(x^n|θ)
P(X=x∣θ)=P(x1∣θ)P(x2∣θ)...P(xn∣θ)
所以
L
(
θ
∣
x
)
=
∏
i
=
1
N
P
θ
(
X
=
x
i
∣
θ
)
L(θ|x)=\displaystyle\prod^{N}_{i=1} P_θ(X=x^{i}|θ)
L(θ∣x)=i=1∏NPθ(X=xi∣θ)
似然函数是一个关于模型参数θ的函数,当选择不同的参数θ时,似然函数的值是不同的,它描述了在当前参数θ下,使用模型分布
P
θ
(
X
=
x
i
∣
θ
)
P_θ(X=x^{i}|θ)
Pθ(X=xi∣θ)产生数据集中所有样本的概率。一个朴素的想法是:在最好的模型参数下
θ
M
L
θ_{ML}
θML,产生数据集中的所有样本的概率是最大的,即
θ M L = a r g m a x L ( θ ) θ_{ML}=argmaxL(θ) θML=argmaxL(θ)
但实际在计算机中,多个概率的乘积结果并不方便储存,例如计算过程中可能发生数值下溢的问题,即对比较小的、接近于0的数进行四舍五入后成为0。我们可以对似然函数取对数来缓解该问题,即 l o g [ L ( θ ) ] log[L(θ)] log[L(θ)],并且仍然求解最好的模型参数 θ M L θ_{ML} θML使对数似然函数最大,即
θ M L = a r g m a x l o g [ L ( θ ) ] θ_{ML}=argmaxlog[L(θ)] θML=argmaxlog[L(θ)]
我们把概率乘积形式转换为对数求和的形式展开
θ M L = a r g m a x ∑ i = 1 N l o g [ P θ ( x i ∣ θ ) ] θ_{ML}=argmax \displaystyle\sum^N_{i=1} log[P_θ(x^i|θ)] θML=argmaxi=1∑Nlog[Pθ(xi∣θ)]
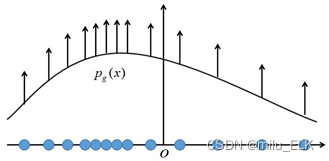
可以发现,使用极大似然估计时,每个样本 x i x_i xi都希望拉高它所对应的模型概率值 p θ ( x i ∣ θ ) p_θ(x^i|θ) pθ(xi∣θ),如图所示,但是由于所有样本的密度函数 p θ ( x i ∣ θ ) p_θ(x^i|θ) pθ(xi∣θ)的总和必须是1,所以不可能将所有样本点都拉高到最大的概率;一个样本点的概率密度函数值被拉高将不可避免的使其他点的函数值被拉低,最终的达到一个平衡态。
我们也可以将上式除以N,便可以看到极大似然法最大化的目标是在经验分布 p d a t a p_{data} pdata下样本概率对数的期望值,即
θ M L = a r g m a x E p d a t a [ l o g P θ ( x i ∣ θ ) ] θ_{ML}=argmax \Bbb E_{p_{data}}[ logP_θ(x^i|θ)] θML=argmaxEpdata[logPθ(xi∣θ)]
此外,最大似然估计和最小KL散度是等价的,我们在下面会提到。
KL散度
KL散度的概念来源于概率论和信息论中。KL散度又被称为:相对熵、互熵、鉴别信息、Kullback熵、Kullback-Leible散度(即KL散度的简写)。在机器学习、深度学习领域中,KL散度被广泛运用于变分自编码器中(Variational AutoEncoder,简称VAE)、EM算法、GAN网络中。
熵
信息论中,某个信息 x i \large x_{i} xi出现的不确定性的大小定义为 x i \large x_{i} xi所携带的信息量,用 I ( x i ) I(x_{i}) I(xi) 表示。 I ( x i ) I(x_{i}) I(xi)与信息 x i \large x_{i} xi 出现的概率 P ( x i ) P(x_{i}) P(xi) 之间的关系为
I ( x i ) = l o g 1 P ( x i ) = − l o g P ( x i ) I(x_i)=log\frac{1}{P(x_i)}=-logP(x_i) I(xi)=logP(xi)1=−logP(xi)
例:掷两枚骰子,求点数和为7的信息量
点数和为7的情况为:(1,6) ; (6,1) ; (2,5) ; (5,2) ; (3,4) ; (4,3) 这6种。总的情况为 6*6 = 36 种。
那么该信息出现的概率为 P x = 7 = 6 36 = 1 6 P_{x=7}=\frac{6}{36}=\frac{1}{6} Px=7=366=61
包含的信息量为 I ( 7 ) = − log P ( 7 ) = − log 1 6 = log 6 I(7)=-\log P(7)=-\log \frac{1}{6}=\log 6 I(7)=−logP(7)=−log61=log6
KL散度(相对熵)
KL散度的定义是建立在熵(Entropy)的基础上的。此处以离散随机变量为例
一个离散随机变量
X
X
X的可能取值为
X
=
x
1
,
x
2
,
.
.
.
x
n
X=x_1,x_2,...x_n
X=x1,x2,...xn,而对应的概率为
P
i
=
P
(
X
=
x
i
)
P_i=P(X=x_i)
Pi=P(X=xi),则随机变量的信息熵定义为:
H
(
X
)
=
−
∑
i
=
1
n
p
(
x
i
)
l
o
g
p
(
x
i
)
H(X)=-\displaystyle\sum^n_{i=1}p(x_i)logp(x_i)
H(X)=−i=1∑np(xi)logp(xi)
规定当 p ( x i ) = 0 时 p(x_i)=0时 p(xi)=0时, p ( x i ) l o g ( p ( x i ) ) = 0 p(x_i)log(p(x_i))=0 p(xi)log(p(xi))=0
相对熵可以用来衡量两个概率分布之间的差异,相对熵越大,差异越大,其性质如下:
-
如果 p(x) 和 q(x) 两个分布相同,那么相对熵等于0
-
D K L ( p ∣ ∣ q ) ≠ D K L ( q ∣ ∣ p ) D_{KL}(p||q)≠D_{KL}(q||p) DKL(p∣∣q)=DKL(q∣∣p),相对熵具有不对称性。
-
D K L ( p ∣ ∣ q ) ≥ 0 D_{KL}(p||q)≥0 DKL(p∣∣q)≥0
如果是两个随机变量P,Q,且概率分布分别为 p ( x ) p(x) p(x), q ( x ) q(x) q(x),则p相对q的相对熵为:
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x ) l o g p ( x ) q ( x ) D_{KL}(p||q)_=\displaystyle\sum^n_{i=1}p(x)log\frac{p(x)}{q(x)} DKL(p∣∣q)=i=1∑np(x)logq(x)p(x)
交叉熵
针对上述离散变量的概率分布 p ( x ) , q ( x ) p(x),q(x) p(x),q(x)而言,其交叉熵定义为:
H ( p , q ) = ∑ x p ( x ) l o g 1 q ( x ) = − ∑ x p ( x ) l o g q ( x ) H(p,q)=\displaystyle\sum_xp(x)log\frac{1}{q(x)}=-\displaystyle\sum_xp(x)logq(x) H(p,q)=x∑p(x)logq(x)1=−x∑p(x)logq(x)
因此根据交叉熵公式,我们可以得出相对熵的公式推导:
D
K
L
(
p
∣
∣
q
)
=
H
(
p
,
q
)
−
H
(
p
)
=
−
∑
x
p
(
x
)
l
o
g
q
(
x
)
−
∑
x
−
p
(
x
)
l
o
g
p
(
x
)
=
∑
x
p
(
x
)
(
l
o
g
q
(
x
)
−
l
o
g
p
(
x
)
)
=
∑
x
p
(
x
)
l
o
g
q
(
x
)
p
(
x
)
D_{KL}(p||q)=H(p,q)-H(p)\\ =-\displaystyle\sum_xp(x)logq(x)-\displaystyle\sum_x-p(x)logp(x)\\ =\displaystyle\sum_xp(x)(logq(x)-logp(x))\\ =\displaystyle\sum_xp(x)log\frac{q(x)}{p(x)}
DKL(p∣∣q)=H(p,q)−H(p)=−x∑p(x)logq(x)−x∑−p(x)logp(x)=x∑p(x)(logq(x)−logp(x))=x∑p(x)logp(x)q(x)
此外,当P,Q为连续变量的时候,KL散度的定义为:
D K L ( p ∣ ∣ q ) = ∫ x p ( x ) [ l o g ( p ( x ) q ( x ) ) ] d x D_{KL}(p||q)=\int_xp(x)[log(\frac{p(x)}{q(x)})]dx DKL(p∣∣q)=∫xp(x)[log(q(x)p(x))]dx(其实和上式是一样的)
最小化相对熵 D K L ( p ∣ ∣ q ) D_{KL}(p||q) DKL(p∣∣q) 等价于最小化交叉熵 H ( p , q ) H(p,q) H(p,q) 也等价于最大似然估计(具体参考Deep Learning 5.5)。在机器学习中,我们希望训练数据上模型学到的分布 P(model) 和真实数据的分布 P(real) 越接近越好,所以我们可以使其相对熵最小。
拓展:条件熵
条件熵 H ( p ∣ q ) H(p|q) H(p∣q)表示在已知随机变量 q 的条件下随机变量 p 的不确定性。条件熵 H ( p ∣ q ) H(p|q) H(p∣q)定义为 p 给定条件下 q 的条件概率分布的熵对 p 的数学期望
条件熵 H ( p ∣ q ) H(p|q) H(p∣q)相当于交叉熵 H ( q , p ) H(q,p) H(q,p)减去单独的熵 H ( q ) H(q) H(q),即 H ( p ∣ q ) = H ( q , p ) − H ( q ) H(p|q)=H(q,p)−H(q) H(p∣q)=H(q,p)−H(q)
高斯分布(正态分布)
若随机变量
X
X
X服从一个数学期望为
μ
μ
μ,方差为
σ
2
σ^2
σ2的正态分布,则记为
X
∼
N
(
μ
,
σ
2
)
X\sim N(μ,σ^2)
X∼N(μ,σ2),其中期望
μ
μ
μ代表了其中心位置,标准差
σ
σ
σ决定了分布的幅度,概率分布的形状类似钟形,当
μ
=
0
μ=0
μ=0,
σ
=
1
σ=1
σ=1时称其服从标准正态分布
N
(
0
,
1
)
N(0,1)
N(0,1)。
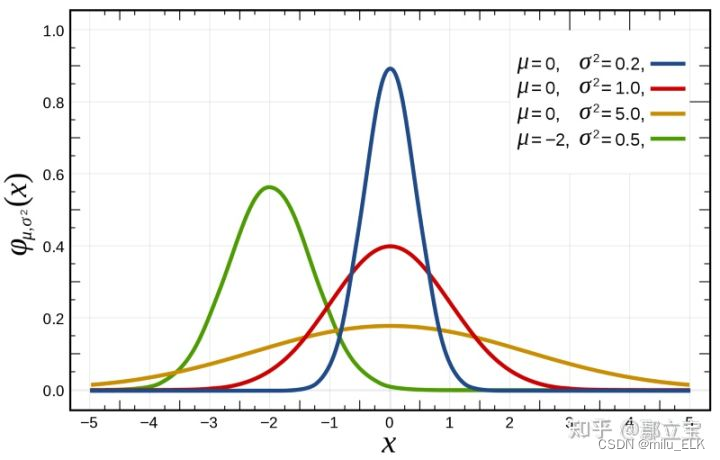
正态分布
:
f
(
x
)
=
1
σ
2
π
e
x
p
(
−
(
x
−
μ
)
2
2
σ
2
)
正态分布:f(x)=\frac{1}{σ\sqrt{2\pi}}exp(-\frac{(x-μ)^2}{2σ^2})
正态分布:f(x)=σ2π1exp(−2σ2(x−μ)2)
标准正态分布
:
f
(
x
)
=
1
σ
2
π
e
x
p
(
−
x
2
2
)
标准正态分布:f(x)=\frac{1}{σ\sqrt{2\pi}}exp(-\frac{x^2}{2})
标准正态分布:f(x)=σ2π1exp(−2x2)
性质:
- 集中性:正态曲线的高峰位于正中央,即均数所在的位置。
- 对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与横轴相交。
- 均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
- 曲线与横轴间的面积总等于1,相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。
马尔可夫链
简述马尔可夫链【通俗易懂】
马尔科夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程,该过程要求具备“无记忆性 ”,即下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。
马尔科夫链认为过去所有的信息都被保存在了现在的状态下了 。比如这样一串数列 1 - 2 - 3 - 4 - 5 - 6,在马尔科夫链看来,6 的状态只与 5 有关,与前面的其它过程无关。
数学定义
则假设我们的序列状态是
.
.
.
X
t
−
2
,
X
t
−
1
,
X
t
,
X
t
+
1
.
.
...X_{t-2},X_{t-1},X_{t},X_{t+1}..
...Xt−2,Xt−1,Xt,Xt+1..,那么在
X
t
+
1
X_{t+1}
Xt+1时刻的状态的条件概率仅依赖于前一刻的状态
X
t
X_t
Xt,即:
P
(
X
t
+
1
∣
.
.
.
X
t
−
2
,
X
t
−
1
,
X
t
)
=
P
(
X
t
+
1
∣
X
t
)
P(X_{t+1}|...X_{t-2},X_{t-1},X_t)=P(X_{t+1}|X_t)
P(Xt+1∣...Xt−2,Xt−1,Xt)=P(Xt+1∣Xt)
既然某一时刻状态转移的概率只依赖于它的前一个状态 ,那么我们只要能求出系统中任意两个状态之间的转换概率,就能确定马尔科夫链的模型。
转移概率矩阵
通过马尔科夫链的模型转换,我们可以将事件的状态转换成概率矩阵 (又称状态分布矩阵 ),如下例:
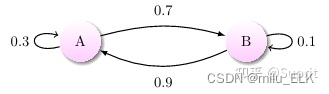
上图中有 A 和 B 两个状态,A 到 A 的概率是 0.3,A 到 B 的概率是 0.7;B 到 B 的概率是 0.1,B 到 A 的概率是 0.9。初始状态在 A,如果我们求 2 次运动后状态还在 A 的概率是多少?很简单:
P
=
A
→
A
→
A
+
A
→
B
→
A
=
0.3
∗
0.3
+
0.7
∗
0.9
=
0.72
P=A\to A\to A+A\to B \to A=0.3*0.3+0.7*0.9=0.72
P=A→A→A+A→B→A=0.3∗0.3+0.7∗0.9=0.72
如果求 2 次运动后的状态概率分别是多少?初始状态和终止状态未知时怎么办呢?这是就要引入转移概率矩阵 ,可以非常直观的描述所有的概率。

并且状态矩阵存在一个性质
- 每行概率之和一定为1
状态转移矩阵(转移概率矩阵)的稳定性
状态转移矩阵有一个非常重要的特性,经过一定有限次数序列的转换,最终一定可以得到一个稳定的概率分布 ,且与初始状态概率分布 t 0 t_0 t0无关。
假设我们当前股市的概率分布为: [ 0.3 , 0.4 , 0.3 ] [0.3,0.4,0.3] [0.3,0.4,0.3],即 30% 概率的牛市,40% 概率的熊盘与 30% 的横盘。然后这个状态作为序列概率分布的初始状态 t 0 t_0 t0,将其带入这个状态转移矩阵计算 t 1 , t 2 , t 3 . . . t_1,t_2,t_3... t1,t2,t3...的状态。代码如下:
matrix = np.matrix([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]], dtype=float)
vector1 = np.matrix([[0.3, 0.4, 0.3]], dtype=float)
for i in range(100):
vector1 = vector1 * matrix
print('Courrent round: {}'.format(i+1))
print(vector1)
输出结果:
Current round: 1
[[ 0.405 0.4175 0.1775]]
Current round: 2
[[ 0.4715 0.40875 0.11975]]
Current round: 3
[[ 0.5156 0.3923 0.0921]]
Current round: 4
[[ 0.54591 0.375535 0.078555]]
。。。。。。
Current round: 58
[[ 0.62499999 0.31250001 0.0625 ]]
Current round: 59
[[ 0.62499999 0.3125 0.0625 ]]
Current round: 60
[[ 0.625 0.3125 0.0625]]
。。。。。。
Current round: 99
[[ 0.625 0.3125 0.0625]]
Current round: 100
[[ 0.625 0.3125 0.0625]]
可以发现,从第 60 轮开始,我们的状态概率分布就不变了,一直保持62.5% 的牛市,31.25% 的熊市与 6.25% 的横盘。
这是因为马尔可夫链只依赖于它的前一个状态,也就是 t 1 t_1 t1依赖 t 0 t_0 t0, t 2 t_2 t2依赖 t 1 t_1 t1…随着转换次数越来越多,那么 t 0 t_0 t0对于 t n t_n tn的影响也会越来越小,最终收敛。因此马尔可夫链最后总会达到一个稳定的概率分布。
我们记 r i j ( n ) = P ( X n = j ∣ X 0 = i ) r_{ij}(n)=P(X_n=j|X_0=i) rij(n)=P(Xn=j∣X0=i)
此外,马尔可夫还有一个重要的乘法规则特性:
P
(
X
0
,
X
1
,
.
.
.
X
n
)
=
P
(
X
n
∣
X
0
,
.
.
.
X
n
−
1
)
P
(
X
0
,
.
.
.
X
n
−
1
)
.
.
.
.
=
P
(
X
0
)
p
i
0
i
1
p
i
1
i
2
.
.
.
p
i
n
−
1
i
n
P(X_0,X_1,...X_n)\\ =P(X_n|X_0,...X_{n-1})P(X_0,...X_{n-1})\\ .... \\ =P(X_0)p_{i_0i_1}p_{i_1i_2}...p_{i_{n-1}i_n}
P(X0,X1,...Xn)=P(Xn∣X0,...Xn−1)P(X0,...Xn−1)....=P(X0)pi0i1pi1i2...pin−1in
如果初始状态
X
0
X_0
X0是给定的,那么可以得到:
P
(
X
1
=
i
1
.
.
.
X
i
n
=
i
n
∣
X
0
=
i
0
)
=
p
i
0
i
1
p
i
1
i
2
.
.
.
p
i
n
−
1
i
n
P(X_1=i_1...X_{i_n}=i_n|X_0=i_0)=p_{i_0i_1}p_{i_1i_2}...p_{i_{n-1}i_n}
P(X1=i1...Xin=in∣X0=i0)=pi0i1pi1i2...pin−1in
实际上马尔可夫链的未来状态 X n + 1 X_{n+1} Xn+1只受到当前状态 X n X_n Xn的影响,而不受到 X n − 1 . . . X 0 X_{n-1}...X_0 Xn−1...X0这些过去状态的影响。
P ( X n + 1 = j ∣ X n , X n − 1 , . . . X 0 ) = P ( X n + 1 ∣ X n ) = p i j P(X_{n+1}=j|X_n,X_{n-1},...X_0)=P(X_{n+1}|X_n)=p_{ij} P(Xn+1=j∣Xn,Xn−1,...X0)=P(Xn+1∣Xn)=pij
状态的区分(Classification of states)
有些状态可能会在访问过一次以后还可以继续访问,但可能有些状态只能访问有限次,那么我们需要对这些状态进行区分。
当 r i j ( n ) > 0 r_{ij}(n)>0 rij(n)>0时,可以说明状态 j j j可以通过 n n n步以后从状态 i i i到达, A ( i ) A(i) A(i)是所有可以由状态 i i i可到达的状态集合,即 ∀ k ∈ A ( i ) , r i k ( n ) > 0 \forall k \in A(i),r_{ik}(n)>0 ∀k∈A(i),rik(n)>0
这里将状态分为了两类:
- Recurrent states(常返状态): ∀ k ∈ A ( i ) \forall k \in A(i) ∀k∈A(i),都有 i ∈ A ( k ) i \in A(k) i∈A(k),即所有可以有状态 i i i到达的状态都可以由该状态出发,经过 n n n步到达状态 i i i 。
- Transient states(瞬时状态): ∃ k ∈ A ( i ) \exists k \in A(i) ∃k∈A(i), i ∉ A ( k ) i \notin A(k) i∈/A(k),即存在可由状态 i i i到达的状态 k k k,无法从该状态到达状态 i i i。
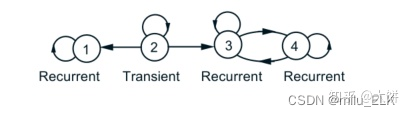
如果状态
i
i
i是recurrent states,那么
A
(
i
)
A(i)
A(i)集合(recurrent class)里所有的状态是互相可达的。
以上图为例, A ( 2 ) A(2) A(2)代表了所有可由状态 2 2 2可到达的状态集合,所以 A ( 2 ) = { 1 , 2 , 3 , 4 } A(2)=\lbrace{1,2,3,4}\rbrace A(2)={1,2,3,4},而其元素是否可通过若干步返回到状态 2 ? 2? 2?我们依次列举:
1 只能到达 1 ( ❌ ) 1只能到达1(❌) 1只能到达1(❌)
2 → 2 ( ⭕ ) 2 \to 2 (⭕) 2→2(⭕)
3 只能到达 3 和 4 ( ❌ ) 3只能到达3和4(❌) 3只能到达3和4(❌)
4 只能到达 3 和 4 ( ❌ ) 4只能到达3和4(❌) 4只能到达3和4(❌)
只要存在一个元素不满足这种返回状态,我们就称其为Transient states,因此 2 2 2是Transient states
同理我们来看 A ( 3 ) A(3) A(3), A ( 3 ) = { 3 , 4 } A(3)=\lbrace{3,4}\rbrace A(3)={3,4}
3 → 3 ( ⭕ ) 3\to 3(⭕) 3→3(⭕)
4 → 3 ( ⭕ ) 4 \to 3(⭕) 4→3(⭕)
因此 3 3 3是Recurrent states
蒙特卡洛方法
蒙特卡罗方法详解
蒙特卡罗方法也称统计模拟方法,是指使用随机数(或者更常见的伪随机数)来解决很多计算问题的方法。他的工作原理就是两件事:不断抽样、逐渐逼近。下面用两个例子来理解一下这个方法的思想。
(1) 圆周率
π
\pi
π值求解
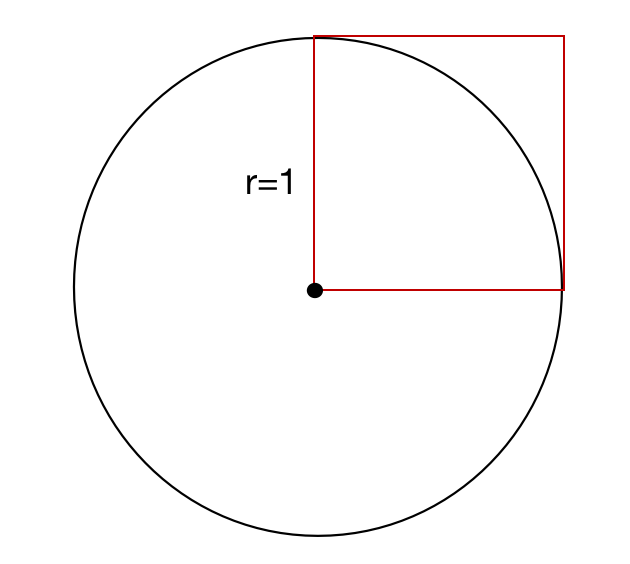
如图所示,有一个半径为r=1的圆和边长为1的正方形,圆的面积为
π
\pi
π,正方形内部相切的面积为
π
4
\frac{\pi}{4}
4π,正方形的面积为1。如果我们向正方形中随机地打点,就会有一定的概率落入圆中,如下图所示:

这样我们就可以得到 落在圆中的概率 = 圆的面积 / 正方形面积 = π 4 落在圆中的概率=圆的面积/正方形面积=\frac{\pi}{4} 落在圆中的概率=圆的面积/正方形面积=4π,也就是说 圆周率 π = 4 ∗ ( 圆的面积 / 正方形的面积 ) = 4 ∗ 落在圆中的概率 圆周率\pi=4*(圆的面积/正方形的面积)=4*落在圆中的概率 圆周率π=4∗(圆的面积/正方形的面积)=4∗落在圆中的概率
因此 π = 4 ∗ 落在圆中的概率 = 4 ∗ ( 红色点数 / 总点数 ) 因此 \pi=4*落在圆中的概率=4*(红色点数/总点数) 因此π=4∗落在圆中的概率=4∗(红色点数/总点数)
如果有足够多的点落入这个图中并将空白处填满,那么最终红色点数将近似于四分之一圆的面积,总点数将近似于正方形的面积,那么理论上我们就可以算出
π
\pi
π,看看在py中的代码计算结果:

可以看出随着随机点数的增加,近似度逐渐增大。
(2) 计算不规则图形面积
比如下面这张黑底图片,想要计算图中白色图形的面积,其中图形都是不规则图形,我们没办法通过边长公式等进行计算,其中一种方法就是可以通过蒙特卡罗方法,向图上随机打点,然后获取像素点所在的颜色,白色面积=白色点数/总点数*图片总面积

通过上面两个例子我们可以理解蒙特卡罗算法的一个基本思想,其实就是通过随机点来模拟实际的情况,不断抽样以逼近真实值。
由蒙特卡洛法得出的值并不是一个精确值,而是一个近似值,而且当投点的数量越来越大时,这个近似值也越接近真实值。
蒙特卡罗方法的应用
通常蒙特卡罗方法可以粗略地分成两类:
一类是所求解的问题本身具有内在的随机性,借助计算机的运算能力可以直接模拟这种随机的过程。
另一种类型是所求解问题可以转化为某种随机分布的特征数,比如随机事件出现的概率,或者随机变量的期望值。通过随机抽样的方法,以随机事件出现的频率估计其概率,或者以抽样的数字特征估算随机变量的数字特征,并将其作为问题的解。这种方法多用于求解复杂的多维积分问题。
蒙特卡罗方法求定积分
假设给出积分
θ
=
∫
a
b
f
(
x
)
d
x
θ=\int ^b_af(x)dx
θ=∫abf(x)dx,如果f(x)的原函数很难求解,那么这个积分也会很难求解。
一个方法是利用蒙特卡罗方法对其进行模拟求解
随机投点法
这个方法和上面的两个例子的方法是相同的。如下图所示,有一个函数f(x),要求它从a到b的定积分,其实就是求曲线下方的面积:
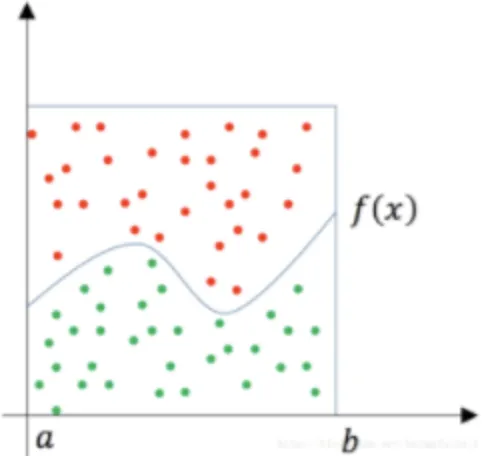
这时可以用一个比较容易算得面积的矩型罩在函数的积分区间上(假设其面积为Area),然后随机地向这个矩形框里面投点,其中落在函数f(x)下方的点为绿色,其它点为红色,然后统计绿色点的数量占所有点(红色+绿色)数量的比例为r,那么就可以据此估算出函数f(x)从 a 到 b 的定积分为 Area × r(总面积*投点比例)。
平均值法(期望法)
如下图所示,在[a,b]之间随机取一点x时,它对应的函数值就是f(x),我们要计算 θ = ∫ a b f ( x ) d x θ=\int ^b_af(x)dx θ=∫abf(x)dx,就是图中阴影部分的面积
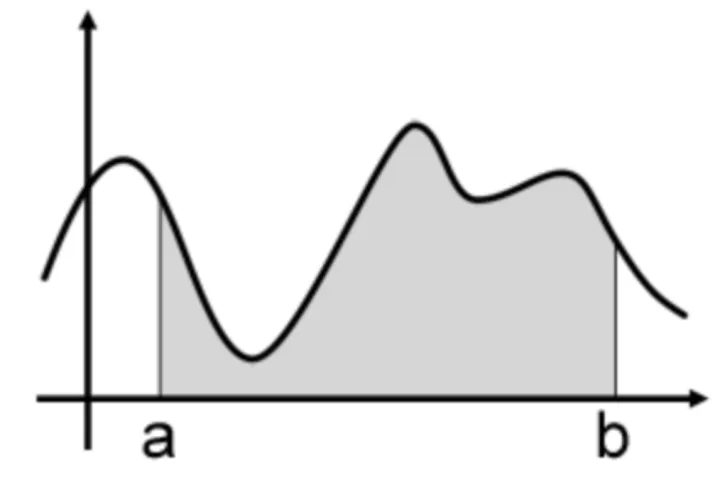
一个简单的近似求解方法就是用
f
(
x
)
∗
(
b
−
a
)
f(x)*(b-a)
f(x)∗(b−a)来粗略估计曲线下方的面积,在[a,b]之间随机取点x,用f(x)代表在[a,b]上所有f(x)的值,如下图所示:
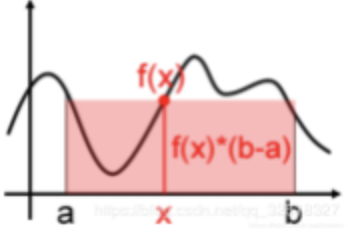
用一个值代表[a,b]区间上所有的f(x)的值太粗糙了,我们可以进一步抽样更多的点,比如下图抽样了四个随机样本
x
1
,
x
2
,
x
3
,
x
4
(
满足均匀分布
)
x_1,x_2,x_3,x_4(满足均匀分布)
x1,x2,x3,x4(满足均匀分布),每个样本都能求出一个近似面积值
f
(
x
)
∗
(
b
−
a
)
f(x)*(b-a)
f(x)∗(b−a),然后计算他们的数学期望,就是蒙特卡罗计算积分的平均值法了。
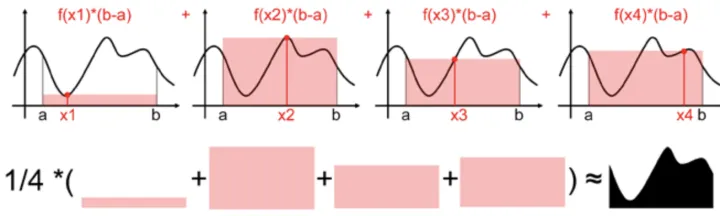
用数学公式表述上述过程:
S
=
b
−
a
4
∑
i
=
1
4
f
(
x
i
)
S=\frac{b-a}{4}\sum^4_{i=1}f(x_i)
S=4b−a∑i=14f(xi)
如果我们采样了n个样本(满足均匀分布),则有:
S
=
b
−
a
n
∑
i
=
1
n
f
(
x
i
)
≃
θ
S=\frac{b-a}{n}\sum^n_{i=1}f(x_i)\simeq θ
S=nb−a∑i=1nf(xi)≃θ
如果采样的样本越多,其估计值也越近似于精确值。但是仍然有个问题:
上面的方法是假定x在[a,b]间是均匀分布的,而大多时候x在[a,b]上不是均匀分布的,因此上面方法就会存在很大的误差。
这时我们假设x在[a,b]上的概率密度函数为 p ( x ) = 1 b − a ( 均匀分布 ) p(x)=\frac{1}{b-a}(均匀分布) p(x)=b−a1(均匀分布),那么S可变换为:
S
=
b
−
a
n
∑
i
=
1
n
f
(
x
i
)
=
b
−
a
n
∑
i
=
1
n
f
(
x
i
)
p
(
x
)
p
(
x
)
=
1
n
∑
i
=
1
n
f
(
x
i
)
p
(
x
)
≃
θ
=
∫
a
b
f
(
x
)
d
x
S=\frac{b-a}{n}\sum^n_{i=1}f(x_i)\\ =\frac{b-a}{n}\sum^n_{i=1}\frac{f(x_i)}{p(x)}p(x)\\ =\frac{1}{n}\sum^n_{i=1}\frac{f(x_i)}{p(x)}\\ \simeq θ=\int ^b_af(x)dx
S=nb−a∑i=1nf(xi)=nb−a∑i=1np(x)f(xi)p(x)=n1∑i=1np(x)f(xi)≃θ=∫abf(x)dx
因此得出结论
1
n
∑
i
=
1
n
f
(
x
i
)
p
(
x
)
≃
∫
a
b
f
(
x
)
d
x
\frac{1}{n}\sum^n_{i=1}\frac{f(x_i)}{p(x)} \simeq \int ^b_af(x)dx
n1∑i=1np(x)f(xi)≃∫abf(x)dx
此处补充一个结论:
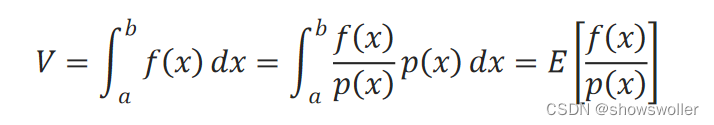
对约等号左边求数学期望:
E
[
1
n
∑
i
=
1
n
f
(
x
i
)
p
(
x
)
]
=
1
n
∑
i
=
1
n
E
(
f
(
x
i
)
p
(
x
)
)
=
1
n
∑
i
=
1
n
f
(
x
)
p
(
x
)
p
(
x
)
d
x
=
1
n
∑
i
=
1
n
f
(
x
)
d
x
=
∫
a
b
f
(
x
)
d
x
\Bbb E[\frac{1}{n}\sum^n_{i=1}\frac{f(x_i)}{p(x)}]\\ =\frac{1}{n}\sum^n_{i=1}\Bbb E(\frac{f(x_i)}{p(x)})\\ =\frac{1}{n}\sum^n_{i=1}\frac{f(x)}{p(x)}p(x)dx\\ =\frac{1}{n}\sum^n_{i=1}f(x)dx=\int^b_af(x)dx
E[n1∑i=1np(x)f(xi)]=n1∑i=1nE(p(x)f(xi))=n1∑i=1np(x)f(x)p(x)dx=n1∑i=1nf(x)dx=∫abf(x)dx
这就是蒙特卡罗方法的一般形式
1
n
∑
i
=
1
n
f
(
x
i
)
p
(
x
)
≃
∫
a
b
f
(
x
)
d
x
\frac{1}{n}\sum^n_{i=1}\frac{f(x_i)}{p(x)} \simeq \int ^b_af(x)dx
n1∑i=1np(x)f(xi)≃∫abf(x)dx
那么问题就换成了如何从p(x)中进行采样。
因此蒙特卡罗方法的目的在于:
对于难以求解的原函数,我们虽然无法求解,但是可以通过蒙塔卡罗方法进行随机抽样,模拟出原函数的近似结果
蒙特卡罗采样方法
常见的概率分布采样
在均匀分布U(0,1)中采样是十分容易通过计算机实现的,针对常见的概率分布都可以通过均匀分布来进行采样,比如下面这个正态分布(当然一般正态分布也不需要通过这种方法,就是为了更好的说明)的概率密度曲线PDF,我们绘制它的累计概率分布曲线CDF:
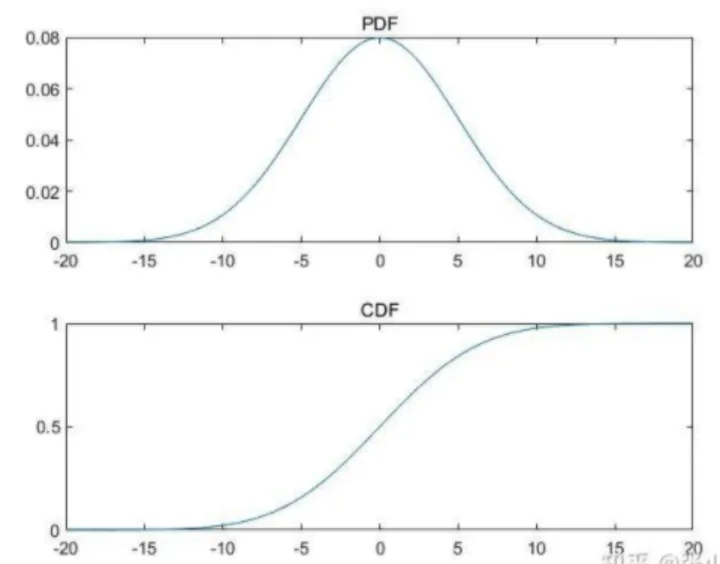
CDF曲线的纵轴是从0到1的,我们可以从均匀分布U(0,1)中采样一个点,然后计算其CDF的反函数,就能得到我们需要的样本点x:
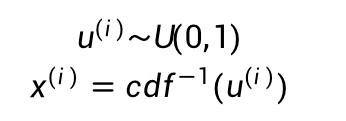
1
n
∑
i
=
1
n
f
(
x
i
)
p
(
x
)
\frac{1}{n}\sum^n_{i=1}\frac{f(x_i)}{p(x)}
n1∑i=1np(x)f(xi)或者我们直接求出PDM这个概率密度函数p(x)代入求解。
但是很多情况下f(x)并不是常见的概率分布,或者是个高维分布,我们就很难生成样本,因此对于复杂概率分布我们会选择接受拒绝采样
接受拒绝采样(取舍采样)
当待采样函数fx)的形式十分复杂时,可以找一个简单的建议分布g(x),使得 C ∗ g ( x ) ≥ f ( x ) C*g(x)\geq f(x) C∗g(x)≥f(x),并将其乘一个常数C使其全部在f(x)的上方,如下图所示,红线是我们要采样的f(x),蓝色曲线为C*g(x), C ∗ g ( x ) C*g(x) C∗g(x)要包裹f(x):
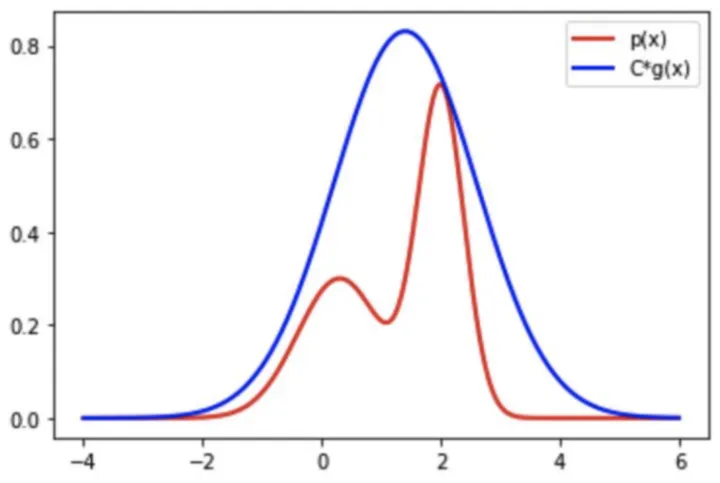
虽然我们从复杂的
f
(
x
)
f(x)
f(x)中采样不容易,但是我们从简单的
C
∗
g
(
x
)
C*g(x)
C∗g(x)中采样是容易的。接受拒绝方法就是利用了更为简单的采样函数来替代
f
(
x
)
f(x)
f(x),然后我们进行随机采样,当采样点在红色曲线下方,就接受它,如果在红色曲线和蓝色曲线中间,就拒绝这个点。当C*g(x)越接近q(x)时接受率越高,采样效率越高,因此有时他们差距比较大时,就会出现大部分的点都被拒绝,这样效率会非常低。

我们将接受率记为
α
=
f
(
x
(
i
)
)
C
g
(
x
(
i
)
)
,
0
≤
α
≤
1
α=\frac{f(x^{(i)})}{Cg(x^{(i)})},0 \leq \alpha \leq 1
α=Cg(x(i))f(x(i)),0≤α≤1
第一步:先通过建议分布
g
(
x
)
g(x)
g(x)产生样本
x
(
i
)
∼
g
(
x
)
x^{(i)}\sim g(x)
x(i)∼g(x)
第二步:产生满足均匀分布的样本
u
(
i
)
∼
U
(
0
,
1
)
u^{(i)}\sim U(0,1)
u(i)∼U(0,1)
第三步:如果
u
≤
α
u \leq α
u≤α,即
u
≤
f
(
x
(
i
)
)
C
g
(
x
(
i
)
)
u \leq \frac{f(x^{(i)})}{Cg(x^{(i)})}
u≤Cg(x(i))f(x(i)),则接受
X
(
i
)
X^{(i)}
X(i),反之拒绝:即为
1
−
α
1-\alpha
1−α
马尔可夫链蒙塔卡罗采样(MCMC)
我们在上面已经讲过了马尔可夫链的知识。
在这里,我们用
π
(
x
)
\pi(x)
π(x)表示马尔可夫链的平稳分布序列,我们知道马尔可夫链在若干步之后一定会收敛,因此,如果满足矩阵方程:
π
=
π
P
\pi=\pi P
π=πP,则称
π
\pi
π为马尔可夫链的平稳分布(其中
P
P
P代表的是状态转移矩阵),这个条件称为稳定平衡条件
我们进一步拓展,如果满足
π
(
i
)
P
(
i
,
j
)
=
π
(
j
)
P
(
j
,
i
)
\pi(i)P(i,j)=\pi(j)P(j,i)
π(i)P(i,j)=π(j)P(j,i),即
i
的状态概率
∗
i
到
j
的状态转移概率
=
j
的状态概率
∗
j
到
i
的状态转移概率
i的状态概率*i到j的状态转移概率=j的状态概率*j到i的状态转移概率
i的状态概率∗i到j的状态转移概率=j的状态概率∗j到i的状态转移概率
我们将上述条件称为细致平衡条件
π
(
i
)
P
(
i
,
j
)
=
π
(
j
)
P
(
j
,
i
)
\pi(i)P(i,j)=\pi(j)P(j,i)
π(i)P(i,j)=π(j)P(j,i),如果满足细致平衡条件,那么一定满足稳定平衡条件
π
=
π
P
\pi=\pi P
π=πP
Metropolis算法
那么针对刚才讲的细致平衡条件,我们想要随机地抽取,随机的给出一个转移矩阵Q(称之为提议矩阵),使得
π
(
i
)
Q
(
i
,
j
)
=
π
(
j
)
Q
(
j
,
i
)
\pi(i)Q(i,j)=\pi(j)Q(j,i)
π(i)Q(i,j)=π(j)Q(j,i)满足,显然是不可能的,结果注定是
π
(
i
)
Q
(
i
,
j
)
≠
π
(
j
)
Q
(
j
,
i
)
\pi(i)Q(i,j)\neq \pi(j)Q(j,i)
π(i)Q(i,j)=π(j)Q(j,i)
但是我们可以引入接受概率
α
\alpha
α,使得
P
(
i
,
j
)
=
Q
(
i
,
j
)
α
(
i
,
j
)
P(i,j)=Q(i,j)\alpha(i,j)
P(i,j)=Q(i,j)α(i,j),
P
(
j
,
i
)
=
Q
(
j
,
i
)
α
(
j
,
i
)
P(j,i)=Q(j,i)\alpha(j,i)
P(j,i)=Q(j,i)α(j,i)
这样就有
π
(
i
)
Q
(
i
,
j
)
α
(
i
,
j
)
=
π
(
j
)
Q
(
j
,
i
)
α
(
j
,
i
)
\pi(i)Q(i,j)\alpha(i,j) = \pi(j)Q(j,i)\alpha(j,i)
π(i)Q(i,j)α(i,j)=π(j)Q(j,i)α(j,i),这样的话我们就可以随机来选取这个矩阵Q了
那如果满足了稳定平衡条件,我们就可以根据 π = π P \pi=\pi P π=πP得出以下条件:
- α ( i , j ) = π ( j ) Q ( j , i ) \alpha(i,j) = \pi(j)Q(j,i) α(i,j)=π(j)Q(j,i)
- α ( j , i ) = π ( i ) Q ( i , j ) \alpha(j,i) = \pi(i)Q(i,j) α(j,i)=π(i)Q(i,j)
但是呢,这个矩阵Q是我们随机选取的,因此有没有可能不存在满足上述条件的接受概率
α
\alpha
α呢?当然是有可能的。也就是说我们随机选取的这个矩阵Q,有可能有接受概率,也有可能没有这个接受概率。Q不一定能等于P,但是有一定概率等于P。
那我们只要接受可以等于P的Q,拒绝不能等于P的Q就行了。是不是有点熟悉?这不正是我们之前讲到的接受拒绝采样(取舍采样)吗?所以Metropolis算法和接受拒绝采样是相似的。不一样的地方在于它是马尔可夫链中的采样,这一时态的样本会影响下一时态。
Metropolis-Hastings 采样算法
Metropolis-Hastings 采样算法改进了接受概率 α \alpha α的选择:
α ( i , j ) = m i n { π ( j ) Q ( j , i ) π ( i ) Q ( i , j ) , 1 } \alpha(i,j)=min\lbrace{\frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1}\rbrace α(i,j)=min{π(i)Q(i,j)π(j)Q(j,i),1}
具体怎么得到的只能各位自行百度了。
总结
MCMC的步骤:
- 给定任意转移矩阵Q,平稳分布 π ( x ) \pi(x) π(x)
- t=0,随机产生一个初始状态 x 0 x_0 x0
- 从条件概率分布 Q ( x ∣ x 0 ) Q(x|x_0) Q(x∣x0)中采样 x ∗ x^* x∗
- 从均匀分布产生 u ∼ U ( 0 , 1 ) u \sim U(0,1) u∼U(0,1)
- 若 u < α ( x 0 , x ∗ ) = m i n { π ( j ) Q ( j , i ) π ( i ) Q ( i , j ) , 1 } u<\alpha(x_0,x^*)=min\lbrace{\frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1}\rbrace u<α(x0,x∗)=min{π(i)Q(i,j)π(j)Q(j,i),1},接受 x ∗ → t = 1 , x 1 = x ∗ x^* \to t=1,x_1=x^* x∗→t=1,x1=x∗
- 否则拒绝该次采样, t = 1 , x 1 = x 0 t=1,x_1=x_0 t=1,x1=x0
- 重复上述粗体步骤,直到t>T时达到平衡(T时刻达到平稳分布)
- t > T t>T t>T之后的所有接受样本即为需要的平稳分布样本
推荐视频蒙特卡洛(Monte Carlo, MCMC)方法的原理和应用