paper：Decoupled Knowledge Distillation

code：https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/DKD.py

背景

与基于响应logits-based的蒸馏方法相比，基于特征feature-based的蒸馏方法在各种任务上的表现更好，因此对基于响应的知识蒸馏的研究越来越少。然而，基于特征的方法的训练成本并不令人满意，因为在训练期间引入了额外的计算和存储占用（如网络模块和复杂的操作）来提取特征。基于响应的蒸馏所需的计算和存储都较小，但性能较差。直觉上来说，logit-based蒸馏方法应当达到与feature-based方法相当的性能，因为logits处与更深的层有更丰富的语义特征。作者猜测logit-based蒸馏的性能受到了未知原因的限制，导致表现不理想。

本文的创新点

本文作者深入研究了KD的作用机制，将分类预测拆分为两个层次：（1）对目标类和所有非目标类进行二分类预测。（2）对每个非目标类进行多分类预测。进而将原始的KD损失也拆分为两部分，一种是针对目标类的二分类蒸馏，另一种是针对非目标类的多分类蒸馏。并分别称为target classification knowledge distillation（TCKD）和non-target classification knowledge distillation（NCKD）。通过分别单独研究两部分对性能的影响，作者发现NCKD中包含了重要的知识，而原始KD对两部分耦合的方式抑制了NCKD的作用，也限制了平衡这两部分的灵活性。

为了解决这些问题，本文提出了一种新的logit蒸馏方法Decoupled Knowledge Distillation（DKD），将TCKD和NCKD进行解耦，使得它们之间的权重可调，从而解除了对NCKD的抑制，提升了蒸馏的性能。

方法介绍

Reformulating KD

Notions

对于一个属于第 \(t\) 类的样本，分类概率可以表示为 \(\mathbf{p}=[p_{1},p_{2},...,p_{t},...,p_{C}]\in \mathbb{R}^{1\times C}\)，其中 \(p_{i}\) 是第 \(i\) 类的概率，\(C\) 是类别数。\(\mathbf{p}\) 中的每个元素都可以通过softmax函数得到

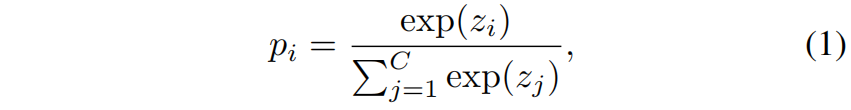
其中 \(z_{i}\) 表示第 \(i\) 类的logit。

为了将与目标类相关和无关的预测分开，定义 \(\mathbf{b}=[p_{t},p_{\setminus t}]\in \mathbb{R}^{1\times 2}\) 表示二分类概率，其中 \(p_{t}\) 表示目标类的概率，\(p_{\setminus t}\) 表示非目标类的概率（所有其它类的概率和），可按下式分别计算得到

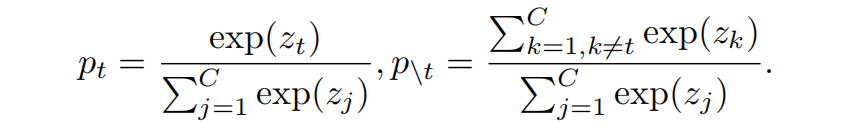
同时定义 \(\hat{\mathbf{p}}=[\hat{p}_{1},...,\hat{p}_{t-1},\hat{p}_{t+1},...,\hat{p}_{C}]\in \mathbb{R}^{1\times (C-1)}\) 来单独建模非目标类别的概率（即不考虑第 \(t\) 类），其中每个元素按下式得到

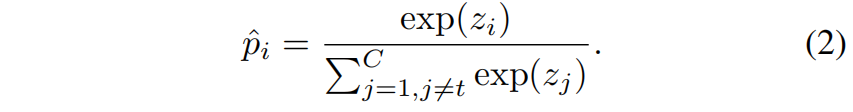
Reformulation

\(\mathcal{T}\) 和 \(\mathcal{S}\) 分别表示教师和学生网络，根据上面定义的二分类概率 \(\mathbf{b}\) 和非目标类的多分类概率 \(\hat{\mathbf{p}}\)，原始KD中的KL散度损失函数可以重写成下面的形式

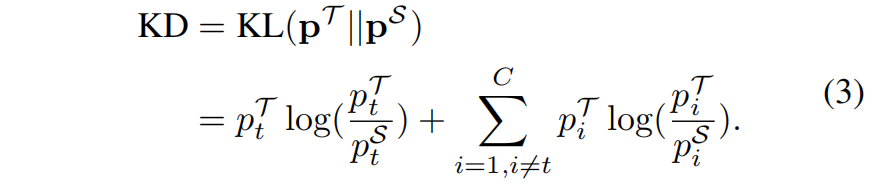
根据式(1)和(2)，我们有 \(\hat{p}_{i}=p_{i}/p_{\setminus t}\)，式(3)可以重写成如下

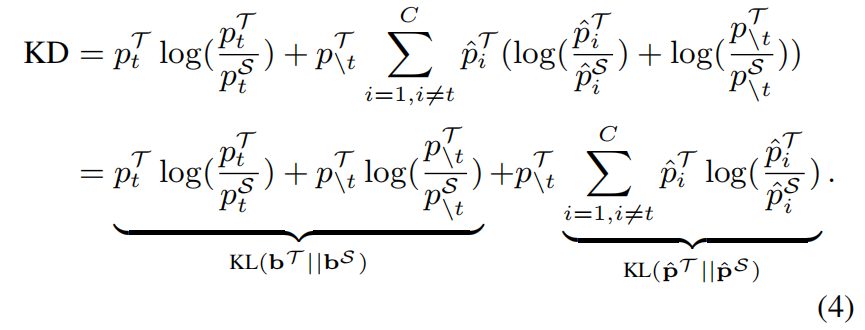
然后式(4)又可以重写成如下

这里根据式(1)(2)(3)推导式(4)(5)的具体过程如下

由式(5)可以看出，KD loss可以看作两项的加权和，其中第一项表示教师和学生网络对目标类别预测概率之间的相似性，因此称之为Target Class Knowledge Distillation(TCKD)。第二项表示教师和学生网络对非目标类别预测概率之间的相似性，称为Non-Target Class Knowledge Distillation(NCKD)。因此式(5)可以重写成如下

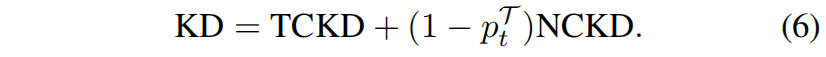
显然，NCKD和 \(p_{t}^{\mathcal{T}}\) 是耦合的。

Effects of TCKD and NCKD

Performance gain of each part

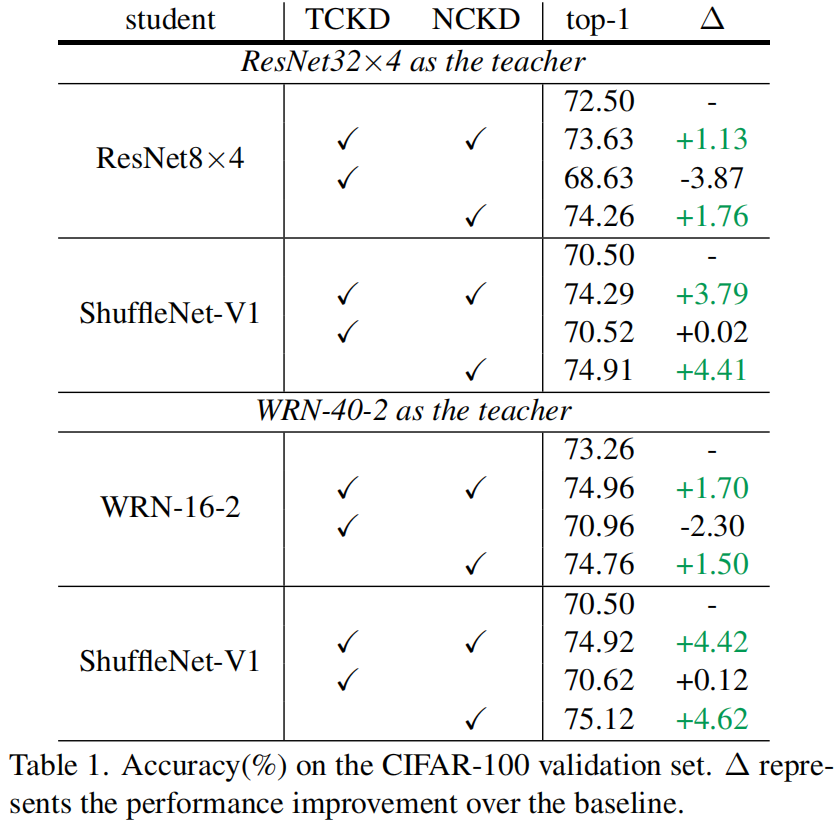
作者在CIFAR-100数据集上分别研究了TCKD和NCKD的影响，结果如下表所示，可以看出，单独使用TCKD对学生模型的提升非常小甚至还会降低精度，而单独使用NCKD可以得到与完整KD相似甚至更高的精度，由此可以看出相比于TCKD，NCKD对学生网络精度的提升更加重要。

TCKD transfers the knowledge concerning the “difficulty” of training samples.

根据式(5)推测TCKD可能将关于样本“难度”的知识传递给了学生网络，例如，相比于 \(p_{t}^{\mathcal{T}}=0.75\) 的样本 \(p_{t}^{\mathcal{T}}=0.99\) 的样本对学生网络来说是更容易学习的样本。由于TCKD传递了样本的难度知识，推测当训练样本更难时TCKD的有效性就会彰显出来，因为CIFAR-100的数据比较简单，TCKD包含的难度知识也相对较少，因此作者通过三个角度进行实验，来验证观点：训练样本越难，TCKD提供的难度知识就越有用。

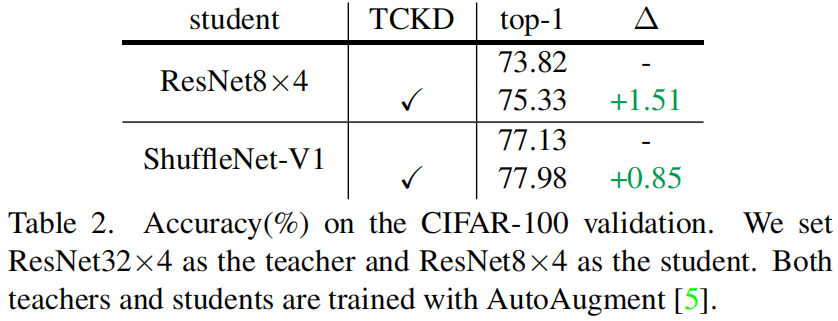
数据增强是一种增加训练样本难度很直接的方法，作者对CIFAR-100进行了AutoAugment增强，然后进行蒸馏的结果如下所示，可以看出进行数据增强后，TCKD对性能的提升更加明显。

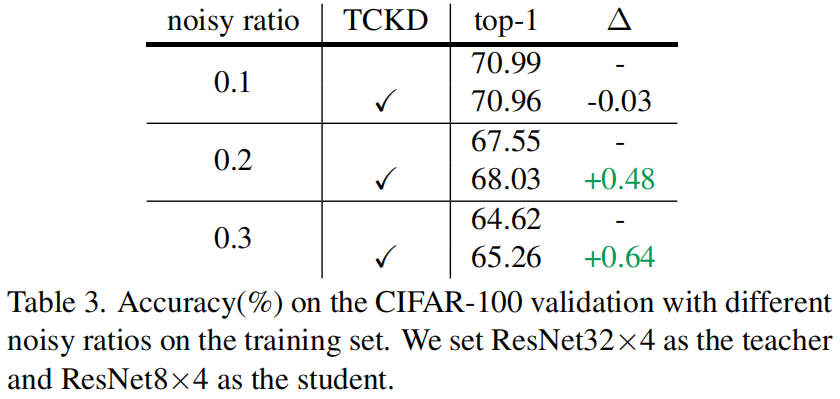
噪声标签也会增加数据的训练难度，对数据添加噪声标签后结果如下所示，结果表明TCKD在噪声更大的训练数据上获得了更大的性能提升。

作者还考虑了更难的数据集比如ImageNet，在ImageNet上TCKD获得了0.32的性能提升。

通过上述实验，作者证明了TCKD在困难数据上的有效性，当在更困难的样本上进行蒸馏时，关于样本难度的知识更有用。

NCKD is the prominent reason why logit distillation works but is greatly suppressed.

从表(1)中可以看出单独使用NCKD时其性能和完整的KD相当甚至更好，这表明非目标类别的知识对logit蒸馏至关重要。但是从式(5)可以看出，NCKD和 \((1-p_{t}^{\mathcal{T}})\) 耦合，\(p_{t}^{\mathcal{T}}\) 表明教师对目标类别的置信度，因此置信度越高会导致NCKD的权重越小。作者认为教师模型对训练样本的置信度越高，它所能提供的知识应该越可靠越有价值，但实际上高置信度确抑制了损失的权重，因此作者将logit蒸馏性能不高的原因归结为原始的KD损失对NCKD的抑制。

作者设计了一个消融实验来验证预测准确即置信度高的样本确实比置信度低的样本包含更有用的知识。首先根据 \(p_{t}^{\mathcal{T}}\) 对训练样本进行排序，将其均分为两个子集，一个子集包含了 \(p_{t}^{\mathcal{T}}\) 前50%的样本，另一个子集包含 \(p_{t}^{\mathcal{T}}\) 后50%的样本。然后在每个子集上用NCKD训练学生网络来比较性能的增益。结果如下表所示，可以看出，对 \(p_{t}^{\mathcal{T}}\) 50%的样本使用NCKD获得了更好的性能，表明了预测准确的样本确实包含了更丰富的知识。

Decoupled Knowledge Distillation

针对上述问题，作者提出了解耦知识蒸馏Decoupled Knowledge Distillation(DKD)，如下所示

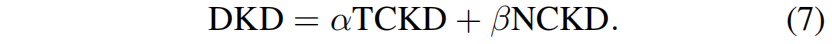
具体来说，引入了超参 \(\alpha\) 和 \(\beta\) 分别作为TCKD和NCKD的权重。

实验结果

下表是采用不同的 \(\alpha\) 和 \(\beta\) 时学生网络的精度，表1中 \(\alpha\) 固定为1.0，表2中 \(\beta\) 固定为8.0。从结果可以看出解耦 \((1-p_{t}^{\mathcal{T}})\) 和NCKD可以带来显著的性能提升（73.64% vs. 74.79%），解耦TCKD和NCKD的权重获得了进一步的性能提升(74.79% vs. 76.32%)。第二个表表明TCKD是不可或缺的，同时当 \(\alpha\) 在1.0附近波动时，TCKD的提升比较稳定没有太大的波动。

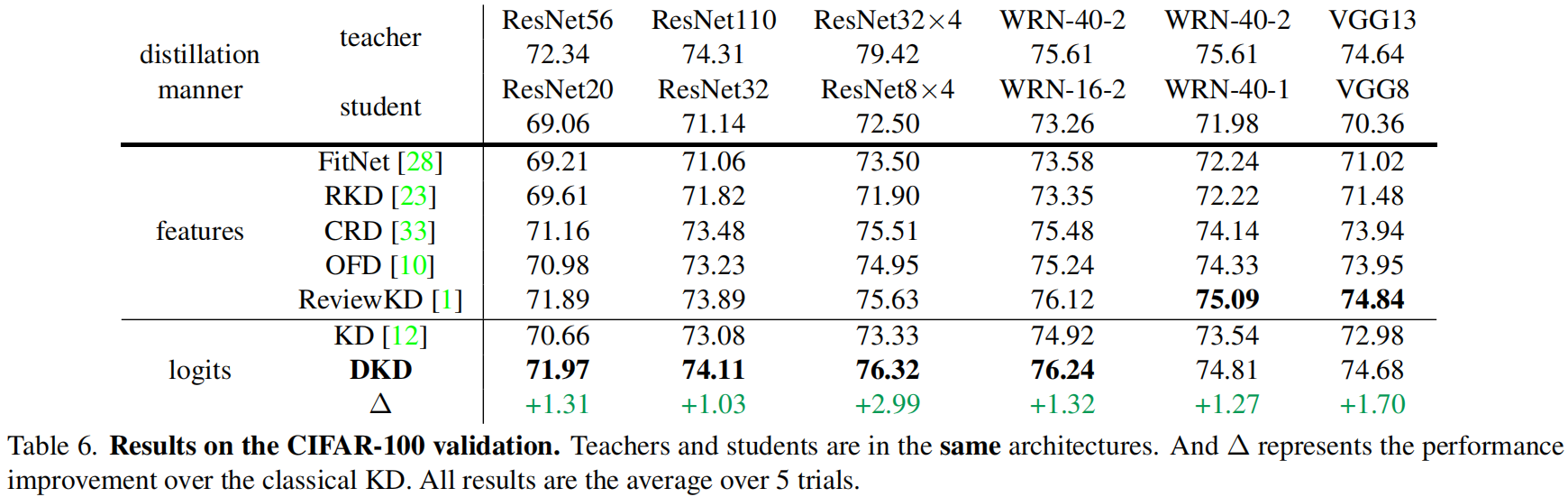
下表是在CIFAR-100验证集上的结果，其中 \(\alpha\) 固定为1，对于不同的教师模型 \(\beta\) 值不同，具体后面会讲。

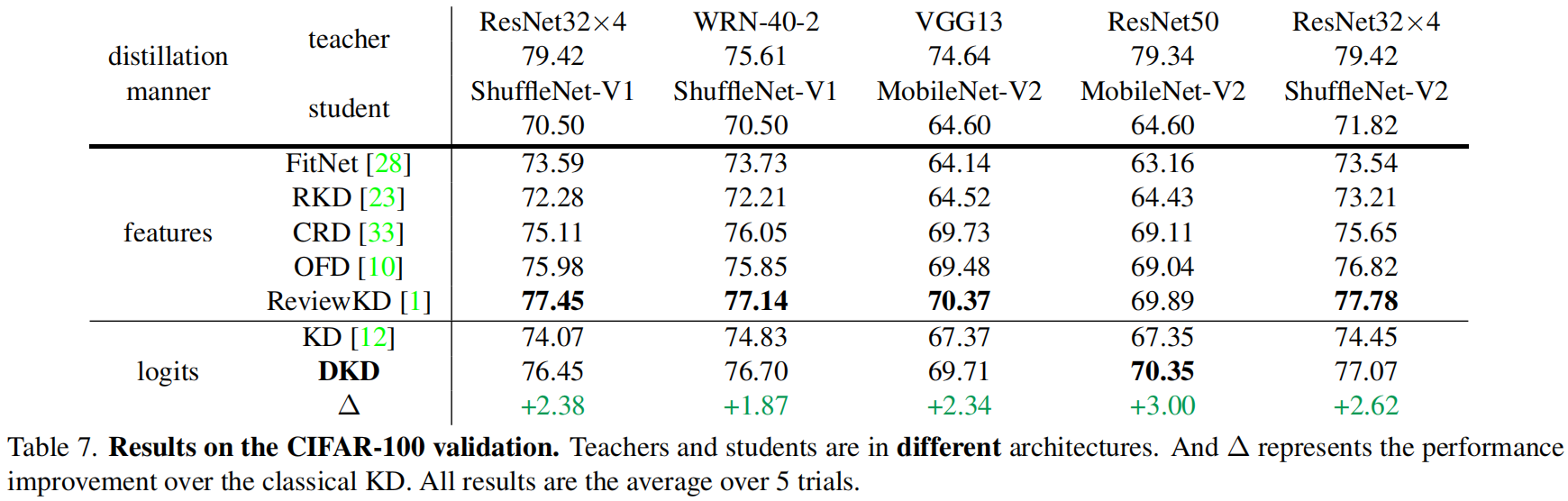
下面是在ImageNet上的结果

Guidance for tuning \(\beta\)

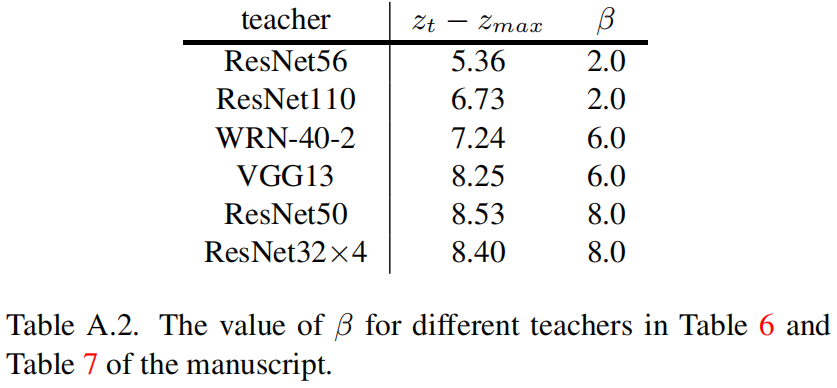
作者认为NCKD在知识传递中的重要性与教师网络的信心有关，教师网络越有信息，NCKD的重要性就越大，\(\beta\) 值就应该越大。如果目标类的logit值远大于所有非目标类，那么可以认为教师非常有信心，\(\beta\) 值也应该设置的更大。因此作者假定 \(\beta\) 值与目标类和所有非目标类之间的logit差有关。目标类的logit用 \(z_{t}\) 表示，其中 \(t\) 表示目标类别，\(z_{max}\) 表示所有非目标类的logit的最大值即 \(z_{max}=max(\left \{ z_{i}|i\ne t \right \} )\)。

作者选用ShuffleNet-v1作为学生网络，比较了选用不同的教师网络和不同的 \(\beta\) 值的精度，并且给出了所有训练样本上 \(z_{t}-z_{max}\) 的均值，结果如下

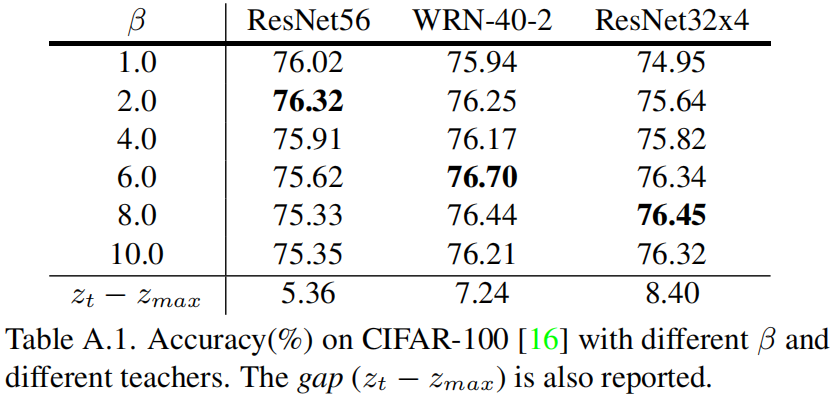
从结果可以看出最优的 \(\beta\) 值与 \(z_{t}-z_{max}\) 成正相关的关系。基于此，表6和表7中不同的教师网络对应的 \(\beta\) 值如下

代码解析

下面是官方实现，其中函数_get_gt_mask中tensor.scatter_()的用法具体见Torch.Tensor.scatter_( ) 用法解读_00000cj的博客-CSDN博客。在求nckd的输入pred_teacher_part2和log_pred_student_part2中都有一个- 1000.0 * gt_mask的操作，这里官方在issue里有解答https://github.com/megvii-research/mdistiller/issues/1，原本的应该是logits[1-gt_mask] / temperature计算所有非目标类别的softmax，因为这里index操作比较慢，因此改成logits/temperature - 1000 * gt_mask，gt_mask中非目标类别处全为0，因此相当于没减。目标类别的logit减去了1000，相当于softmax中分子和分母各加上 \(e^{-1000}\) 约等于0，等价于没加。

import torch
import torch.nn as nn
import torch.nn.functional as F

from ._base import Distiller


def dkd_loss(logits_student, logits_teacher, target, alpha, beta, temperature):
    # (64,100),(64,100),(64),1,8,4
    gt_mask = _get_gt_mask(logits_student, target)  # (64,100),除了每个样本对应target索引处为True, 其它都为False
    other_mask = _get_other_mask(logits_student, target)
    pred_student = F.softmax(logits_student / temperature, dim=1)
    pred_teacher = F.softmax(logits_teacher / temperature, dim=1)
    pred_student = cat_mask(pred_student, gt_mask, other_mask)  # (64,2), 第一列是目标类别的logit, 第二列是所有非目标类别的logit的和
    pred_teacher = cat_mask(pred_teacher, gt_mask, other_mask)
    log_pred_student = torch.log(pred_student)
    tckd_loss = (
        F.kl_div(log_pred_student, pred_teacher, size_average=False)
        * (temperature**2)
        / target.shape[0]
    )
    # https://github.com/megvii-research/mdistiller/issues/1
    # e^{-1000}非常小约等于0，等价于把这一项去掉了
    pred_teacher_part2 = F.softmax(
        logits_teacher / temperature - 1000.0 * gt_mask, dim=1
    )
    log_pred_student_part2 = F.log_softmax(
        logits_student / temperature - 1000.0 * gt_mask, dim=1
    )
    nckd_loss = (
        F.kl_div(log_pred_student_part2, pred_teacher_part2, size_average=False)
        * (temperature**2)
        / target.shape[0]
    )
    return alpha * tckd_loss + beta * nckd_loss


def _get_gt_mask(logits, target):
    target = target.reshape(-1)
    mask = torch.zeros_like(logits).scatter_(1, target.unsqueeze(1), 1).bool()
    return mask


def _get_other_mask(logits, target):
    target = target.reshape(-1)
    mask = torch.ones_like(logits).scatter_(1, target.unsqueeze(1), 0).bool()
    return mask


def cat_mask(t, mask1, mask2):
    t1 = (t * mask1).sum(dim=1, keepdims=True)  # (64,1)
    t2 = (t * mask2).sum(1, keepdims=True)  # (64,1)
    rt = torch.cat([t1, t2], dim=1)  # (64,2)
    return rt


class DKD(Distiller):
    """Decoupled Knowledge Distillation(CVPR 2022)"""

    def __init__(self, student, teacher, cfg):
        super(DKD, self).__init__(student, teacher)
        self.ce_loss_weight = cfg.DKD.CE_WEIGHT
        self.alpha = cfg.DKD.ALPHA
        self.beta = cfg.DKD.BETA
        self.temperature = cfg.DKD.T
        self.warmup = cfg.DKD.WARMUP

    def forward_train(self, image, target, **kwargs):
        logits_student, _ = self.student(image)
        with torch.no_grad():
            logits_teacher, _ = self.teacher(image)

        # losses
        loss_ce = self.ce_loss_weight * F.cross_entropy(logits_student, target)
        loss_dkd = min(kwargs["epoch"] / self.warmup, 1.0) * dkd_loss(
            logits_student,
            logits_teacher,
            target,
            self.alpha,
            self.beta,
            self.temperature,
        )
        losses_dict = {
            "loss_ce": loss_ce,
            "loss_kd": loss_dkd,
        }
        return logits_student, losses_dict