哈希应用：位图

一.提出问题

问题： 给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

先考虑内存的问题：40亿个整数，每个整数4字节，换算大约16G的空间，寻常的查找算法都是不可能完成的。因此引入位图。

二.位图概念

数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在。

通过这种同样是哈希的思想，就可以极大的节省空间，整形范围在0~2³²-1，因此我们可以开2³²个比特位，换算下来只有512M的大小，通过直接映射就能够判断。

我们无法开这么大的数组，但我们采用的是bit位的标记，即值是几，就把第几个位标记成1。

那么如何去找呢？实际上我们把数组的元素类型规定为char(int也可以)，这样就可以通过如下的方式去找任意一个数：x

x映射的值，在第几个char对象上：x/8
x映射的值，在这个char对象的第几个比特位：x%8

比特位顺序问题：

事实上，比特位的顺序与机器的大小端无关，仍是和地址一样从右到左：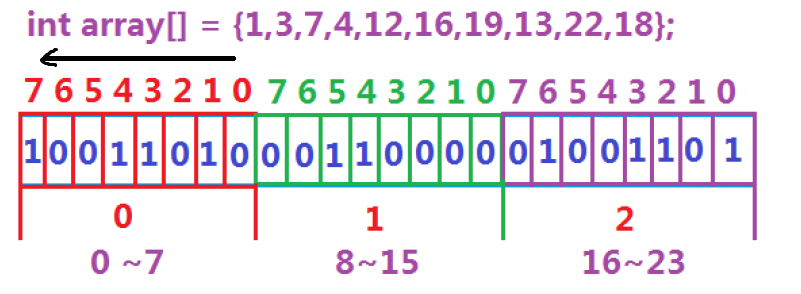

因此在处理定位x在指定char的第几个比特位上时，就需要从右到左去查找。

三.位图代码

对于位图的功能，要有插入，删除，检测在不在三个功能，如果这样赋值：

size_t i = x / 8;
size_t j = x % 8;

插入就可以这样：_bits[i] |= (1 << j);

删除就可以这样：_bits[i] &= (~(1 << j));

测试这个值在不在就可以这样：return _bits[i] & (1 << j);

此外，一开始同样需要开辟指定大小的空间，因此构造函数中要写出来。

template<size_t N>
class cfy_set
{
public:
    void set(size_t x)//标记
    {
        size_t i = x / 8;
        size_t j = x % 8;

        _bits[i] |= (1 << j);

    }
    void reset(size_t x)//清除
    {
        _bits[i] &= (~(1 << j));
    }

    bool test(size_t x)//测试这个值在不在
    {
        size_t i = x / 8;
        size_t j = x % 8;

        return _bits[i] & (1 << j);
    }
private:
    vector<char> _bits;
};

对于测试这个值在不在的返回值，会发生整形提升，因为bool属于int类型，按照符号位的数值进行补位，但是对于逻辑来说不重要。

需要注意的是，由于是无符号数，事实上可以将x/8+1换成(x>>3)+ 1;由于>>的优先级低于+，所以需要加上括号。

测试：

void test_cfy_set()
{
	//cfy_set<100> cs1;
	//cfy_set<-1> cs2;//无符号最大数直接传-1，会转成最大数量
	cfy_set<0xffffffff> cs3;//同上
	cs3.set(10);
	cs3.set(10000);
	cs3.set(8888);

	cout << cs3.test(10) << endl;
	cout << cs3.test(10000) << endl;
	cout << cs3.test(8888) << endl;
	cout << cs3.test(8887) << endl;
	cout << cs3.test(9999) << endl;
}

事实上，库中也有位图结构 bitset ，也可以直接通过库中的位图查找。

四.位图应用

一. 给定100亿个整数，设计算法找到只出现一次的整数？

对于此整数有三种状态：

出现0次
出现1次
出现一次以上

因此，我们可以通过两个比特位来标记：00代表出现0次；01代表出现1次，其他的代表出现一次以上。（两个标记位可以表示从1到3）那么位图会变成这样：在这里插入图片描述

此方式虽然可行，但需要第上述代码做出很大变动。那么我们可以采用另一种方式代表两个比特位，即以开两个位图的方式，每个位图的一个比特位组合成两个比特位进行标记：

因此，通过这种方式及思想我们甚至可以给任意范围的数字进行标记。那么接下来就实现一下：

template<size_t N>
class twobitset
{
public:
	void set(size_t x)//标记
	{
		if (!_bs1.test(x) && !_bs2.test(x))// 00
		{
			//需要变10
			_bs2.set(x);
		}
		else if (!_bs1.test(x) && _bs2.test(x))//10
		{
			_bs1.set(x);
			_bs2.reset(x);//10
		}
		//10不变 

	}

	void PrintOnce()
	{
		for (size_t i = 0; i < N; ++i)
		{
			if (!_bs1.test(i) && _bs2.test(i))
			{
				cout << i << endl;
			}
		}
		cout << endl;
	}
private:
	bitset<N> _bs1;//库里的bitset，当然自己写的也可
	bitset<N> _bs2;
};

void test_twobitset()
{
    twobitset<100> tbs;
    int a[] = { 3, 5, 6, 7, 8, 9 ,33, 55, 67, 3,3,3,5,9,33 };
    for (auto e : a)
    {
        tbs.set(e);
    }
    tbs.PrintOnce();
}