给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

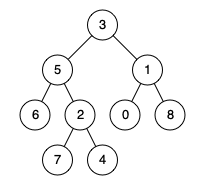
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1

输出：3

解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

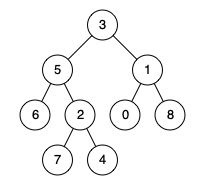
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4

输出：5

解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2

输出：1

提示：

1、树中节点数目在范围 [2, 105] 内。

2、-109 <= Node.val <= 109

3、所有 Node.val 互不相同 。

4、p != q

5、p 和 q 均存在于给定的二叉树中。

思路：

本题使用递归，判断当前结点的左右树是否同时包含p，q，若左树同时包含p，q，左树的左树，不同时包含，那么当前节点的左节点就是最近的公共祖先

代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null){
            return null;
        }
        if(root==p||root==q){
            return root;
        }

        TreeNode leftTree=lowestCommonAncestor(root.left,p,q);
        TreeNode rightTree=lowestCommonAncestor(root.right,p,q);

        if(leftTree!=null&&rightTree!=null){
            return root;
        }
        if(leftTree!=null){
            return leftTree;
        }
        if(rightTree!=null){
            return rightTree;
        }
        return null;
    }
}