文章目录
- 一、深度优先搜索算法
- 二、完整代码示例
- 完整代码示例
- 执行结果
一、深度优先搜索算法
深度优先搜索算法步骤 : 将 深度优先搜索 算法步骤 转为代码 ;
- ① 访问初始结点 : 访问 初始结点 v , 并将该 初始结点 v 标记为 " 已访问 " ; 设置一个 访问标记 数组 , 数组元素个数与 顶点个数相同 ;
/**
* 判定顶点是否被访问
*/
private boolean[] isVisted;
- ② 查找邻接节点 : 查找 初始结点 v 的 第一个 邻接节点 w ;
/**
* 获取结点的第一个邻接结点
* @param index
* @return 如果存在 邻接结点 返回对应下标 , 如果不存在返回 -1
*/
public int getFirstNeighbor(int index) {
for (int i = 0; i < vertexList.size(); i++) {
if (edges[index][i] > 0) {
return i;
}
}
return -1;
}
- ③ 邻接节点是否存在 :
- 如果 w 结点存在 , 执行 ④ 操作 判断该 结点 是否被访问 ;
- 如果 w 结点 不存在 , 回到 ① 查找 初始结点 v 的下一个 邻接节点 ;
/**
* 已知 v1 结点有一个邻接结点 v2, 找到 v2 之后的下一个 v1 的邻接结点
* @param v1
* @param v2
* @return 如果找到邻接结点 返回其索引 , 反之返回 -1
*/
public int getNextNeighbor(int v1, int v2) {
for (int i = v2 + 1; i < vertexList.size(); i++) {
if (edges[v1][i] > 0) {
return i;
}
}
return -1;
}
- ④ 邻接节点是否被访问 :
- 如果 w 结点存在 并且 没有被访问 , 那么 对 w 结点 进行 深度优先遍历 , 将 w 结点 作为 新的 初始结点 v , 从 ① 步骤开始执行 ;
- 如果 w 结点存在 但是 被访问了 , 那么 查找 w 结点的 下一个 邻接节点 , 转到步骤 ③ 执行 ;
/**
* 递归核心函数, 给定一个初始结点, 找到其第一个邻接结点, 如果该邻接结点没有被访问,
* 将新结点作为 初始结点 , 进行递归遍历
* @param isVisted
* @param i
*/
public void dfs(boolean[] isVisted, int i) {
// 访问初始结点
System.out.println("Visit Vertex : " + getVertexByIndex(i));
// 设置 i 结点已访问
isVisted[i] = true;
// 查找 i 结点的第一个邻接结点 w
int w = getFirstNeighbor(i);
// 如果不存在 第一个邻接结点 则返回 -1
// 如果存在 , 返回 该结点 索引
while (w != -1) {
// 确保找到的 第一个 邻接结点 没有访问过
if (!isVisted[w]) {
// 以 w 为初始结点 , 进行递归
dfs(isVisted, w);
}
// 如果 第一个 邻接结点 已访问
// 那么找到 i 作为初始结点 , w 作为 第一个邻接结点 , 之后的 第二个邻接结点
w = getNextNeighbor(i, w);
}
}
遍历的入口函数 : 一般情况下只需要一个结点 , 就可以将所有的结点遍历完毕 ;
/**
* 遍历入口函数
*/
public void dfs() {
for (int i = 0; i < getNumberOfVertex(); i++) {
if (!isVisted[i]) {
dfs(isVisted, i);
}
}
}
二、完整代码示例
完整代码示例
import java.util.ArrayList;
import java.util.Arrays;
public class Graph {
/**
* 图顶点
*/
private ArrayList<String> vertexList;
/**
* 图的邻接矩阵
*/
private int[][] edges;
/**
* 图中边的数据
*/
private int numOfEdges;
/**
* 判定顶点是否被访问
*/
private boolean[] isVisted;
/**
* 构造器
* @param n 顶点个数
*/
public Graph(int n) {
// 创建 n x n 邻接矩阵
edges = new int[n][n];
// 初始化顶点容器
vertexList = new ArrayList<>(n);
// 边数量统计
numOfEdges = 0;
// 顶点是否被访问标志位
isVisted = new boolean[n];
}
/**
* 插入顶点
* @param vertex 顶点名称
*/
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
/**
* 插入边
* @param v1 起始顶点索引
* @param v2 终止顶点索引
* @param weight 顶点的权重
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
// 边的数量增加 1
numOfEdges++;
}
/**
* 获取结点个数
* @return
*/
public int getNumberOfVertex() {
return vertexList.size();
}
/**
* 获取边的个数
* @return
*/
public int getNumberOfEdges() {
return numOfEdges;
}
/**
* 获取指定节点的索引值
* @param i
* @return
*/
public String getVertexByIndex(int i) {
return vertexList.get(i);
}
/**
* 获取 v1 到 v2 的权值
* @param v1
* @param v2
* @return
*/
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
/**
* 打印邻接矩阵
*/
public void showGraph() {
for (int i = 0; i < edges.length; i++) {
System.out.println(Arrays.toString(edges[i]));
}
}
/**
* 获取结点的第一个邻接结点
* @param index
* @return 如果存在 邻接结点 返回对应下标 , 如果不存在返回 -1
*/
public int getFirstNeighbor(int index) {
for (int i = 0; i < vertexList.size(); i++) {
if (edges[index][i] > 0) {
return i;
}
}
return -1;
}
/**
* 已知 v1 结点有一个邻接结点 v2, 找到 v2 之后的下一个 v1 的邻接结点
* @param v1
* @param v2
* @return 如果找到邻接结点 返回其索引 , 反之返回 -1
*/
public int getNextNeighbor(int v1, int v2) {
for (int i = v2 + 1; i < vertexList.size(); i++) {
if (edges[v1][i] > 0) {
return i;
}
}
return -1;
}
/**
* 递归核心函数, 给定一个初始结点, 找到其第一个邻接结点, 如果该邻接结点没有被访问,
* 将新结点作为 初始结点 , 进行递归遍历
* @param isVisted
* @param i
*/
public void dfs(boolean[] isVisted, int i) {
// 访问初始结点
System.out.println("Visit Vertex : " + getVertexByIndex(i));
// 设置 i 结点已访问
isVisted[i] = true;
// 查找 i 结点的第一个邻接结点 w
int w = getFirstNeighbor(i);
// 如果不存在 第一个邻接结点 则返回 -1
// 如果存在 , 返回 该结点 索引
while (w != -1) {
// 确保找到的 第一个 邻接结点 没有访问过
if (!isVisted[w]) {
// 以 w 为初始结点 , 进行递归
dfs(isVisted, w);
}
// 如果 第一个 邻接结点 已访问
// 那么找到 i 作为初始结点 , w 作为 第一个邻接结点 , 之后的 第二个邻接结点
w = getNextNeighbor(i, w);
}
}
/**
* 遍历入口函数
*/
public void dfs() {
for (int i = 0; i < getNumberOfVertex(); i++) {
if (!isVisted[i]) {
dfs(isVisted, i);
}
}
}
public static void main(String[] args) {
// 创建图
Graph graph = new Graph(5);
// 添加顶点
graph.insertVertex("A");
graph.insertVertex("B");
graph.insertVertex("C");
graph.insertVertex("D");
graph.insertVertex("E");
// 添加边
graph.insertEdge(0, 1, 1); // AB
graph.insertEdge(0, 2, 1); // AC
graph.insertEdge(1, 0, 1); // BA
graph.insertEdge(1, 2, 1); // BC
graph.insertEdge(1, 3, 1); // BD
graph.insertEdge(1, 4, 1); // BE
graph.insertEdge(2, 1, 1); // CA
graph.insertEdge(2, 2, 1); // CB
graph.insertEdge(3, 1, 1); // DB
graph.insertEdge(4, 1, 1); // EB
// 打印临街矩阵
graph.showGraph();
// 深度优先搜索遍历
graph.dfs();
}
}
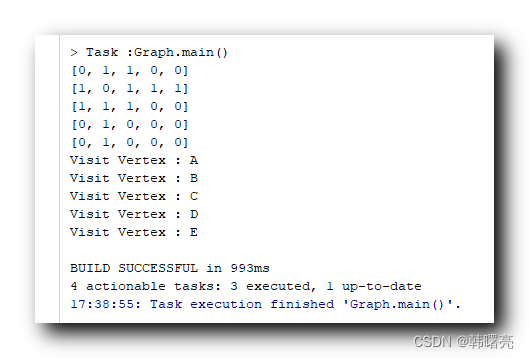
执行结果
> Task :Graph.main()
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 1, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
Visit Vertex : A
Visit Vertex : B
Visit Vertex : C
Visit Vertex : D
Visit Vertex : E