第一题:最短子串
题目描述
米小游拿到了一个字符串,她想截取一个连续子串,使得该子串中包含至少k个连续的“mihoyo”。
你可以帮米小游求出最短的子串长度,以及对应的子串位置吗?
输入描述
第一行输入两个正整数n和k,用空格隔开。
第二行输入一个长度为n的、仅由小写字母组成的字符串。1≤k≤n≤200000
22 2
mihoyoyomihoyomimihoyo
输出描述
如果不存在这样一个连续子串,请输出-1。
否则输出两个正整数l,r,代表选取的子串的左下标和右下标(整个字符串左下标为0,右下标为n-1)。
请务必保证选择的连续子串包含至少k个"mihoyo",且长度是最短的。有多解时输出任意即可。
0 13
代码与测试
#include<iostream>
#include<string>
#include<vector>
#define NMAX 200000
using namespace std;
int n, k;
string S;
vector<pair<int, int>> res;
string standard = "mihoyo";
int main() {
cin >> n >> k >> S;
int p1 = 0, p2 = 0, pre = 0;
for (; p1 < n; p1++) {
if (S[p1] == standard[p2]) {
if (!p2) pre = p1;//若为第一个,记录下来
p2++;
if (p2 == 6) { //若为最后一个,则直接添加到Res中
res.push_back(make_pair(pre, p1));
p2 = 0;
}
}
else p2 = 0;//不相等直接略过
}
/*for (int i = 0; i < res.size(); i++) {
cout << res[i].first << " " << res[i].second << endl;
}*/
int size = NMAX;
pair<int, int> ret;
for (int i = 0; i < res.size(); i++) {
if (i + k > res.size()) break;
if (res[i + k -1].second - res[i].first < size) {
size = res[i + k -1 ].second - res[i].first;
ret.first = res[i].first;
ret.second = res[i + k -1].second;
}
}
if (size == NMAX) cout << -1 << endl;
else cout << ret.first << " " << ret.second << endl;
}
测试用例:
In:
53 2
hsuimihoyomsmihoyoshdusicmihoyomihoyomimimishudmihoyo
Out:
25 36
In:
65 3
hsuimihoyomsmihoyomihoyomihoyoshdusicmihoyomihoyomimimishudmihoyo
Out:
12 29
第二题:猜数字
题目描述
米小游心中想了一个正整数,她邀请了n个人来猜这个数。每个人会猜一个数ai,然后米小游会告诉对方猜的结果:大于等于米小游想的数(≥)或者小于米小游想的数(<)。
猜谜结束后,米小游统计了共有x个≥和y个<。请你判断米小游初始想的数有多少种不同的可能?
输入描述
第一行输入一个正整数n,代表猜谜的人数。
第二行输入n个正整数ai,代表每个人猜的数字。
第三行输入两个整数x和y,用空格隔开。
1≤x+y=n≤1e5,1 ≤ ai ≤ 1e9
3
1 5 3
0 3
输出描述
如果有无穷多种可能,输出"infinity"
否则输出一个整数,代表米小游心中想的数的不同可能数量。
infinity
代码与测试
#include<iostream>
#include<algorithm>
using namespace std;
#define NMAX 100005
int n, x, y;
int num[NMAX];
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> num[i];
cin >> x >> y;
sort(num, num+n);
if (x == n) cout << num[0];
else if (y == n) cout << "infinity";
else cout << num[y] - num[y - 1];
}
In:
3
1 5 3
0 3
Out:
infinity
In:
9
12 32 21 902 12 90 129 12 90
4 5
Out:
58
In:
9
12 32 21 902 12 90 129 12 90
9 0
Out:
12
C++中的sort
第三题:树的连通块
题目描述
米小游有一棵有根树,树上共有n个节点。
米小游指定了一个节点x为根,然后定义所有相邻的、编号奇偶性相同的节点为一个连通块。
米小游想知道,所有子树(共有n个子树)的连通块数量之和是多少?
举个例子:
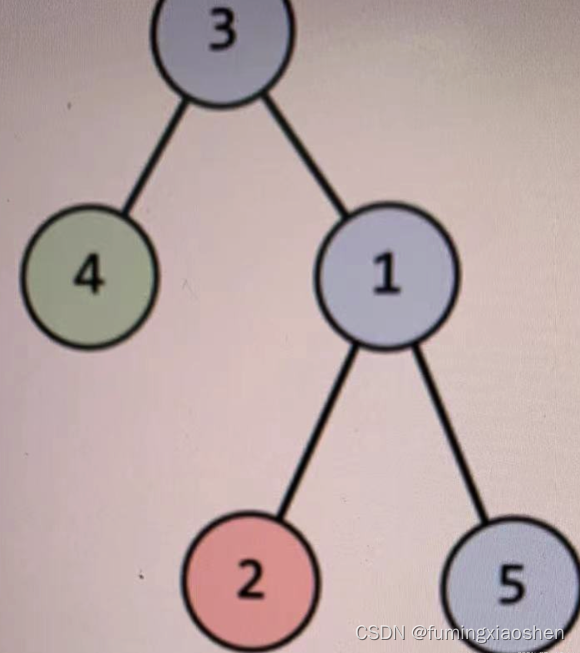
如上图,3号节点被指定为根
然后3-1-5作为一个连通块,4号节点和2号节点为单独的连通块。
那么1号节点到5号节点,每个节点的子树连通块数量分别为:2、1、3、1、1,总连通块数量是8。
输入描述
5 3
1 2
1 3
3 4
5 1
输出描述
8
代码与测试
#include<iostream>
#include<vector>
using namespace std;
int n, root;
#define NMAX 100005
int res = 0;
struct node{
int s = 1;
vector<int> adj;
}T[NMAX];
void dfs(int r, int fa) {
int leaf = 1;
for (int i = 0; i < T[r].adj.size(); i++) {
int son = T[r].adj[i];
if (son == fa) continue;
else {
leaf = 0;
dfs(son, r);
if (son % 2 == r % 2) T[r].s += (T[son].s - 1);
else T[r].s += T[son].s;
}
}
if (leaf) T[r].s = 1;
res += T[r].s;
}
int main() {
int x, y;
cin >> n >> root;
for (int i = 0; i < n - 1; i++) {
cin >> x >> y;
T[x].adj.push_back(y);
T[y].adj.push_back(x);
}
dfs(root,0);
cout << res;
}
In:
5 2
1 2
1 3
3 4
5 1
Out:
9
In:
5 3
1 2
1 3
3 4
5 1
Out:
8
原题链接