约瑟夫问题可以说十分经典，其没有公式解也是广为人知的~

前言

一、约瑟夫问题与逆约瑟夫问题

1.约瑟夫问题

2.逆约瑟夫问题

二、思考与尝试（显然有很多失败）

问题分析

尝试一：递归/递推的尝试

尝试二：条件约束下的求解

尝试三：遍历

尝试四：可行性与最优性剪枝优化

尝试五：可行特解的寻找方法

三、总结评价

四、核心代码

1. x==s情况下，找特解

2. x!=s情况下，找特解（效率很低）

3. 遍历找特解（实话是，实际感觉花费时间很少，比上面好多了）

总结

前言

本博客源于一次作业。老师要求我们逆求约瑟夫问题，着实困扰许久。

一、约瑟夫问题与逆约瑟夫问题

1.约瑟夫问题

有这样一个游戏，n个同学围绕成一个环，分别标号1.2.3...n，并按顺序排列，显然1与2和n相邻。从第s个同学开始以此报数，当报数为m时，报数的同学离开环。剩下的接着从1开始报数，如上循环，直至只剩一人。最后一个人获胜。

约瑟夫问题的解法有很多，递归/模拟是两个大类。在这里的解法就不赘述了。

2.逆约瑟夫问题

假设你正在游玩约瑟夫游戏，从你开始报数，游戏规则与课上讲述一致，现在你想确保你是最后一个，即获胜的玩家。如果由你设置m（即每报几个数出列一人），你应该如何设置m来确保自己的胜利？

二、思考与尝试（显然有很多失败）

问题分析：

正常的约瑟夫问题，由人数n，报数长m，开始位次s，来推导出最终出列的人编号x。求解过程是自然、顺势而为的。而此约瑟夫进阶问题，则是通过最终出列人的编号、开始位次（固定从第一个开始）、人数n来求得报数长m。是逆着自然进行的操作，所以预测是困难的。为此我进行了一些尝试，试图得出解析解，但显然这与约瑟夫问题本身一样，解析解是不可能的。其他的一些尝试，虽然都历经了失败，但是对于问题本身有了更加深入的理解，对于朴素方法——枚举判断m，有了一些优化的考量。

尝试一：递归/递推的尝试

从正向的约瑟夫问题出发，约瑟夫问题可以被精妙地转化为递归问题，将复杂的情况转化为规模小的问题。逆约瑟夫问题同样是有着较大规模、较类似的子问题。因此尝试讲逆约瑟夫问题转化为递归问题。然而，在尝试中遇到了困难。

设，为了求得m，考虑低复杂度的子问题，即当或n小到问题可以求解，是必备的条件。此外，还需要问题能够往低阶过渡，即公式可以写成的形式。经过思考，发现这两种条件都无法满足。

同时，由于m、n、x在同一问题的解中的唯一性，很难将类似于往更高的进行递推，尝试用递推也困难重重。

尝试二：条件约束下的求解

对于固定的n、x，都有m与之对应，那么n、x对于m有何等约束呢？

约瑟夫问题是一个环问题，对这一类问题，有一种解法普遍适用。那就是将环拆成链，把这条链复制后首位连接，这就达到了化环为链的效果。只是约瑟夫问题下，对于一段链上“踢出该成员”的操作，对于所有的子链上对应的成员，都要进行“踢出”操作。于是想到，用操作的长度的不同表示，来对m进行限制。

设共k+1段子链，那么操作长度length通过子链个数与位置x来计算有：

同时，从踢人的轮数z以及考虑到踢出不被计数因此实际跳过的人数c考虑有：

因此总有：

然而仔细观察结构，总有一组特解使上式成立：

由于c的不可确定性，采用对c、k、z遍历的方法，尝试找到满足使m为整数的解，发现只能得出以上特解。

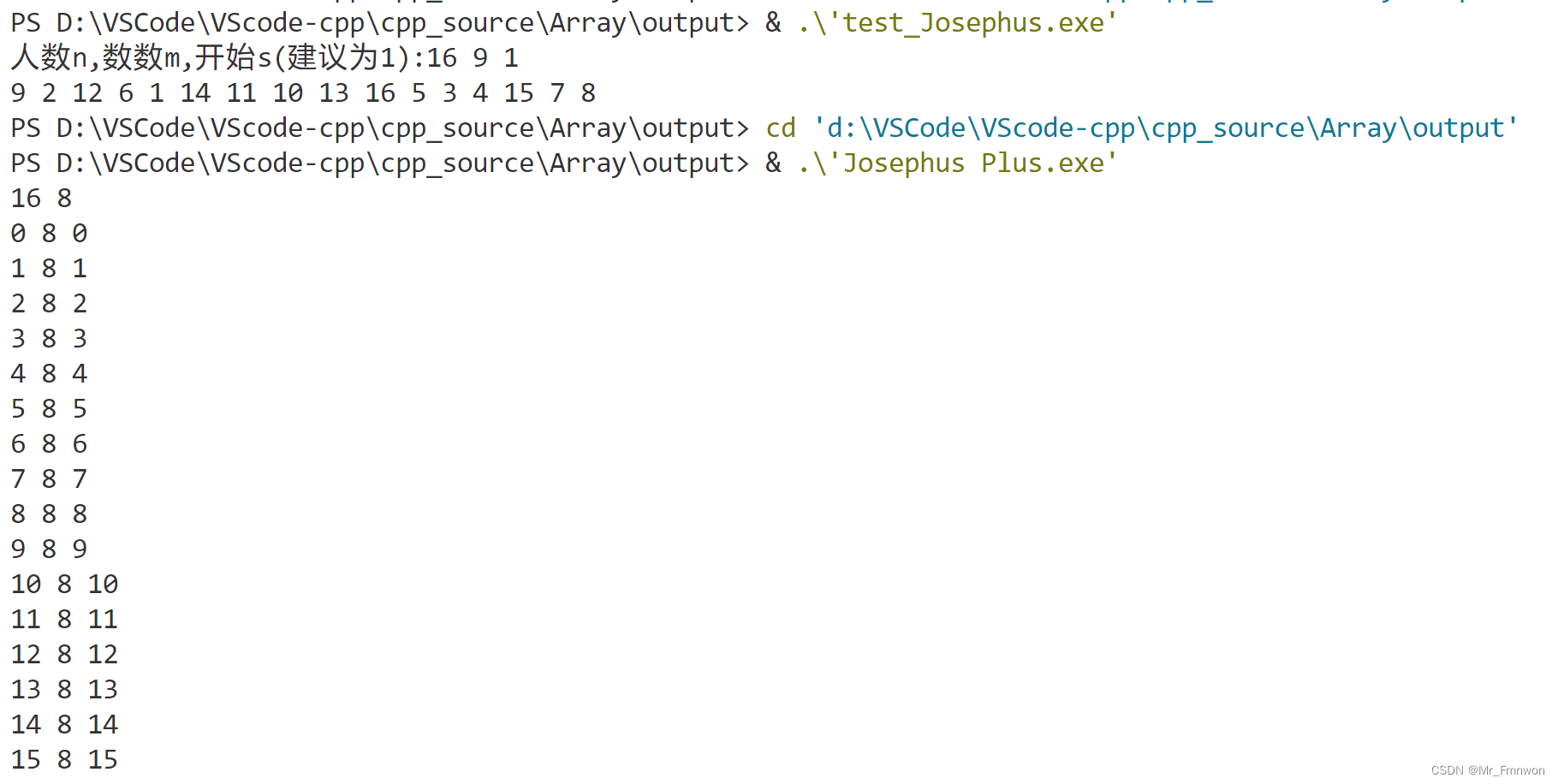
因此，如此考虑，实际上也是无意义的。

尝试三：遍历

为此，从以上两次尝试，可以发现，正面解决逆约瑟夫问题，不亚于反面解决约瑟夫问题。其实，最朴素最简单的一类想法，就是遍历。我们已经解决了在给定n、s、m求x的问题，在解决给定n、s=1、x求m的问题时，可以通过遍历m的可能取值，将得出来的x与给定的x进行比较。如果相等，就说明此时的m是合理的，或者说此时的m就是答案。

下面对这种方法进行复杂度分析。

考虑最好情况，即m第一次取值就是答案，此时复杂度为一次约瑟夫问题求解的复杂度，O(n2)。最坏的情况下，可能要取n次，复杂度为O(n3)。平均复杂度也为O(n3)。由于遍历的方法是基于多次的约瑟夫问题求解，时间复杂度比较高。这也是为什么一开始不从遍历枚举这种最朴素直接可行的方法着手的原因。

从约瑟夫问题本身过程考虑，结合逆约瑟夫问题的要求，考虑进一步优化的方法。

尝试四：可行性与最优性剪枝优化

注意到逆约瑟夫问题的要求，即最后一名出队的同学是给定的x。这意味着如若x不是最后一个出队，那么此时进行评测的m也不是符合要求的答案。对逆约瑟夫问题的求解，就好比是一棵具有n个枝的树，某一些枝不可能得到答案，就直接将其抛弃。因此我们可以对原约瑟夫问题进行可行性剪枝，来实现对逆约瑟夫问题的优化。此外，如若已经找到可行的m使得问题得解，就不需要继续进行后续m+1、m+2……的评判了。认定第一个m就是最优答案，不去考虑剩下的答案，即为最优性剪枝。

具体剪枝策略：

对于每一位出列的人，同时记录出列的总的数量。如若x出列且出列的人总数不为n，即还有人未出列、x不是最后一个出列，此时就直接终止当前约瑟夫问题求解过程，并转入对m+1的约瑟夫问题解的判定。此外，找到一个答案，直接退出求解序列。

程序求解

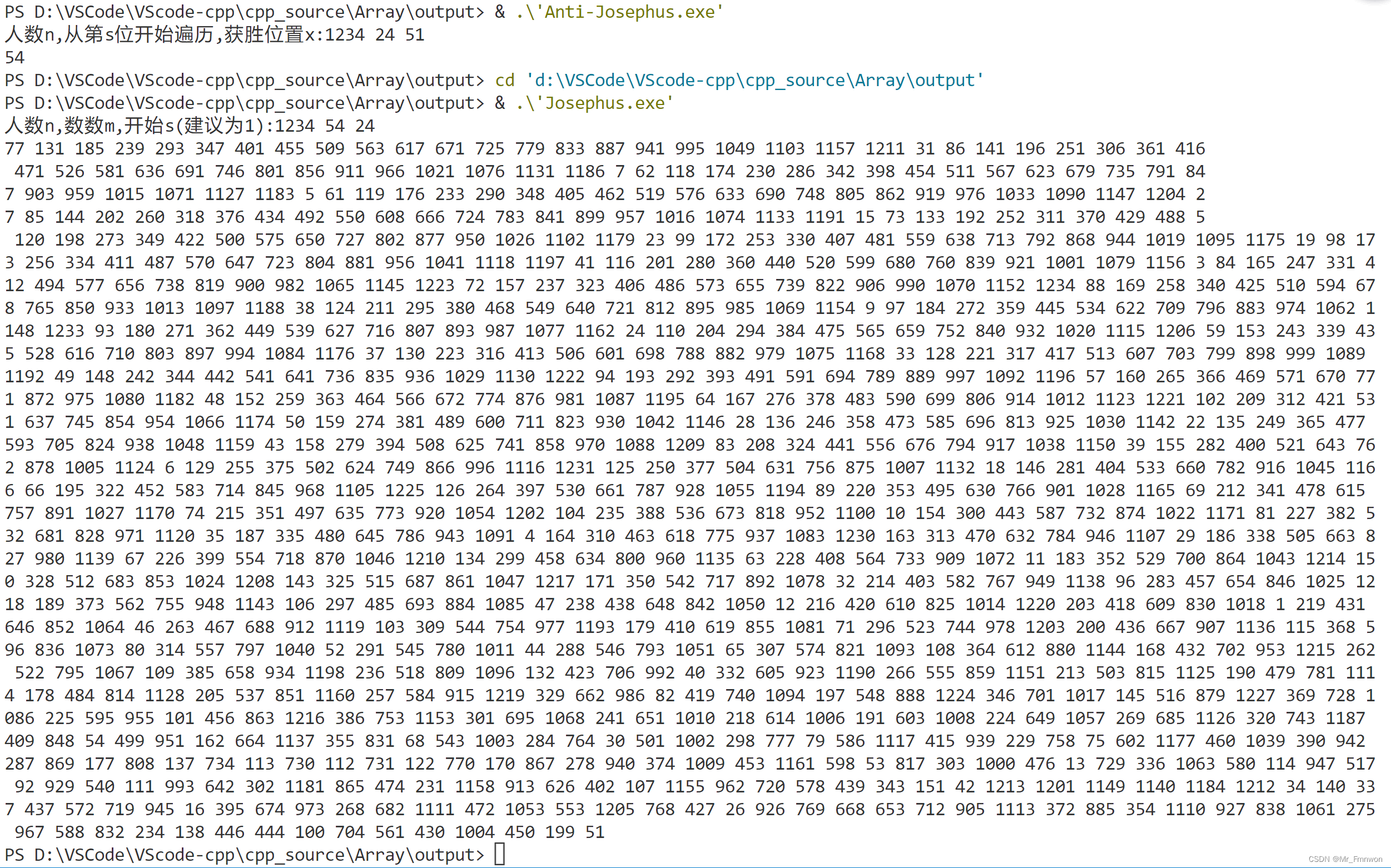
运行编写好的程序，随机输入人数n、开始位次s、获胜位置x，求解m。

这里随机取n=1234 s=24 x=51 程序“Anti-Josephus.exe”解得m=54

然后用约瑟夫问题程序“Josephus.exe”进行检验：输入n=1234,m=54,s=24，可以看到，最后一个出列的是51，与答案相等。其他几次测试也都如此。

当然，对于某些特定的n、s、x，不存在m使得其成立。

（实际上，由于人会退出，所以m>n也是合理的，因为m=m%n不成立。因此，由无穷的m对应有限的n，几乎可以说任何一个位置都由多个m作为解。这里的程序在尝试的时候，下意识认为m<=n，是有问题的。不过，之后的尝试过程中都修正过来了）

尝试五：可行特解的寻找方法

本来已经提交作业。课上，老师说已经交的部分作业他看过了，绝大多数都是遍历。于是他做了一些提示。给同学们的思路开拓作用很大。事实上，寻求特解这一思路，之前竟一直没有出现在我的脑海中。

上课教员给予了一种新的思路，或者说对题目的含义有了更为精确的理解：第x位次的人为获胜，需要找到m使得他获胜。由于约瑟夫问题跳过了已经点名过的人，或者说，已经点名过的人已经被踢出序列。因此，并不意味着km+b=b的成立。所以，可以说，m的值域远远超过人数n。

然而最后一名获胜者只有一个，只有n种可能。这就意味着，有多个不同的m使得第x位的人获胜。而我们只需要求出一个，这一个可以是平凡普通解，也可以是特解。寻求通解的算法/公式，难度很高，上述也进行了多次尝试。然鹅，寻求特解，意味着我们可以用一些规律，找到那些富有某种特征的解。

考察游戏进行到最后只剩两个人的情况。若由第x个位置的人开始报数，那么需要报2/4/6…即2的倍数次，即可获胜。若由另一个人开始报数，那么需要报1/3/5…即奇数次，位置x的人即可获胜。为了方便求解，我们考虑从x位置的人首先报数的情况。之所以认为选择x开始报数这种情况优于另一种，是因为：可以将小规模的问题推广，即，不论多少人，都从首先x开始报数，而每一种规模的问题，都有近似的解法。

约定：①设Ni为倒数第i轮，一共进行n轮。 ②每轮都由x位置首先开始报数。③ $LCM(X,Y,Z...)$ 表示X,Y,Z...的最小公倍数。

i=n时，那么x第n轮出局，有

i=n-1时，x在下一轮出局，为满足约定②，

i=n-2时，还剩三个人，为下一轮满足约定②，

……

i=2时，还有n-1人，为下一轮满足约定②，

i=1时，还有n人，然而第一轮明确规定从s开始报数，为下一轮满足约定②，

或者写成

综合上述n个约束：

只要满足上式两个式子，m就是满足题目含义的一个解。（自然有更多的解不满足条件，但这里只寻求找到解，或者说，找到特解的情况。）

令人欣喜的是：题目中要求从第x人开始报，

那么上式就化为

两式合并为（实际上，这种策略下的最小解即）：

得到这个公式，如果“不顾一切”的话，我们甚至可以O(1)地得到一个特解m地值——n!

然而如果要将m带入程序进行验算，草率地令m=n!常常会导致数太大而程序崩溃（例如C++，只用基本类型，不考虑高精度等算法）。因此，我们需要进行筛选，找到1~n的（最小）公倍数。

值得庆幸的是，我们已经有了最小公倍数的求解算法。不过直接应用还是可能面临时间复杂度太高的问题（n>=25时已经开始凸显）。

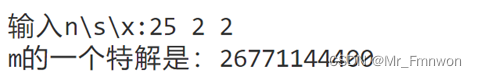
所以，权衡公倍数大小与算法复杂度，给出恰当的解法，是进一步考虑的问题。在此不做讨论。

三、总结评价：

尝试了多种思路，企图找到“捷径”，压缩时间复杂度，可惜失败了。

从朴素的遍历思想出发，能够保证解出问题（m的值或无解），但是时间复杂度令人担忧。

因此，为了尽量压缩时间复杂度，对逆约瑟夫问题的子问题，即单个约瑟夫问题，进行了可行性剪枝与最优性剪枝，尽可能的节省时间开支。

在教员进行提点之后，进行了尝试五，并写出了相应代码。虽然当x!=s的时候效率低下，但对于题目要求s=x而言，速度还是很可观的。不过由于c++类型大小限制，一般n取20左右，已经是运行极限了。（受long long/int类型大小限制。当然，可以通过高精度等算法来改进，但是时间效率依然堪忧）

最后，希望通过拓宽眼界、拓展能力，掌握更多数据结构与算法知识，找到解决逆约瑟夫问题的更好方法。

四、核心代码

1. x==s情况下，找特解

//s==x下的代码
int findM(int n, int s)
{
    typedef unsigned long long ull; 
    ull m1=n;
    for(int i=n-1;i>=2;--i) 
    {
        if(m1%i==0)continue;
        ull a1=m1,a2=i;
        ull c = 0;
        while(c = a1 % a2)
        {
            a1 = a2;
            a2 = c;
        }
        m1=m1*i/a2;
    }
    //cout<<m1<<endl;
    return m1;
}

2. x!=s情况下，找特解（效率很低）

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;

//求最大公约数
inline ll gcd(ll a,ll b) {
    while(b^=a^=b^=a%=b);
    return a;
}
//求a,b的最小公倍数
ll lcm(ll a,ll b);
int main()
{
    ll m1;
    ll n,s,x;
    cout<<"输入n\\s\\x:";		//题目要求，即输入x==s
    cin>>n>>s>>x;
    m1=n-1;
    for(int i=n-2;i>=2;--i) //m0即lcm(1,2,3...n-1)
    {
        if(m1%i==0)continue;
        m1=lcm(m1,i);
    }
    ll m2=x-s;
    while(1)
    {
        if(m2>m1&&m2%m1==0)
        {
            cout<<"m的一个特解是："<<m2<<endl;
            break;
        }
        m2+=n;
    }
    return 0;
}
ll lcm(ll a,ll b)
{
    return a*b/__gcd(max(a,b),min(a,b));
}

3. 遍历找特解（实话是，实际感觉花费时间很少，比上面好多了）

调用了自己编写的Array类，进行约瑟夫问题的模拟。实际上就是将约瑟夫问题迭代多次，修改过来的。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include"Array.h"
#include"Array.cpp"
using namespace std;

void Josephus(Array<int>& P,int n,int m,int x,bool& key,int s)
{
   
    int k=1;
    for(int i=0;i<n;++i){P.Insert(k,i);k++;}
    int s1=s;
    for(int j=n;j>=1;j--)
    {
        s1=(s1+m-1)%j;
        if(s1==0)s1=j;
        if(P.Getnode(s1-1)==x)	//剪枝
        {
          if(j!=1)return;		//可行性剪枝
          else key=true;		//最优性剪枝
        }
        int w=P.Getnode(s1-1);
        P.Remove(s1-1);
        P.Insert(w,n-1);
    }
}

Array<int> a;
int n,s,x;
int main()
{
    cout<<"人数n,从第s位开始遍历,获胜位置x:";
    cin>>n>>s>>x;
    bool key=false;
    int m_ans=0;
    while(!key)				//如果没找到答案，继续评判下一个m
    {
      m_ans++;
      if(m_ans>n)break;
      Josephus(a,n,m_ans,x,key,s);
      a.clear();			//清空a的元素，为下一轮做准备
    }
    if(key)cout<<m_ans;		//如果找到答案，输出它
    else cout<<"No answer!";	//如果没有找到答案，说明无解
    return 0;
}