二进制与十进制转换(包括整数和小数的转换)
二进制转十进制
首先要先了解二进制的含义,与十进制相似,二进制代表的是以
2的次幂在每一位上的0/1表示,平时我们经常接触的都是整数的二进制,是从2的0次幂开始的,其实小数位的表示也是使用的2的次幂,时使用的负数次幂。与之对应的负数次幂就是小数。
⋅ ⋅ ⋅ 2 3 2 2 2 1 2 0 . 2 − 1 2 − 2 2 − 3 2 − 4 ⋅ ⋅ ⋅ ···2^{3} 2^{2} 2^{1}2^{0}.2^{-1}2^{-2}2^{-3}2^{-4}··· ⋅⋅⋅23222120.2−12−22−32−4⋅⋅⋅
对应位置的
0/1表示就是二进制的整数和小数。然后对应位置求和就是十进制。
例:(二)100.01 = (十)4.25
十进制转二进制
十进制转二进制是算法题中经常考察的题目,通常条件下用正常的模拟手法能解决大部分题目,下面介绍模拟的过程(不含代码),也就是十进制转二进制是的计算方法。
整数位部分的转换
整数位十进制转二进制相对于小数位来说还是非常常见的,方法就是
除二取余这里放上一张计算流程图。图中的每一步都是除2的过程,记下余数,倒序书写即为十进制转为二进制。
推理: ⋅ ⋅ ⋅ 2 3 2 2 2 1 2 0 ···2^{3} 2^{2} 2^{1}2^{0} ⋅⋅⋅23222120 每次的除2取余过程都是把 2 0 2^{0} 20 这一位换出去,剩下的次幂都减一,不影响二进制的排列(如101011 -> 10101) 也就变成了 2 0 2^{0} 20 这一位如果是1则余1,否则余0
小数位部分的转换
小数位的十进制转换二进制比较少见,甚至有时候见到这里题目猛地不知道怎么解决(这也是写这篇文章的目的)。与整数位的方法非常相似。小数的十进制可以按对应位置求和来表示 1 2 + 1 4 + 1 8 + 1 16 + 1 32 ⋅ ⋅ ⋅ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32}··· 21+41+81+161+321⋅⋅⋅ 因为第一位
乘2之后能出来整数位的1,并且后面的次幂加1,和整数位的方法相似。此处有个小小的数学证明 1 4 + 1 8 + 1 16 + 1 32 ⋅ ⋅ ⋅ \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32}··· 41+81+161+321⋅⋅⋅ 是小于1 2 \frac{1}{2} 21 的,这也就保证了,只有第一位为1是才能乘2后出现整数位的1。图例是一个小数的转换过程:这里与整数位方法不同的是,我们每次
乘2后的计算结果就按小数点后第一位开始填写。并且每次乘2后出现整数位1后要减去1之后再进行接下来的运算。
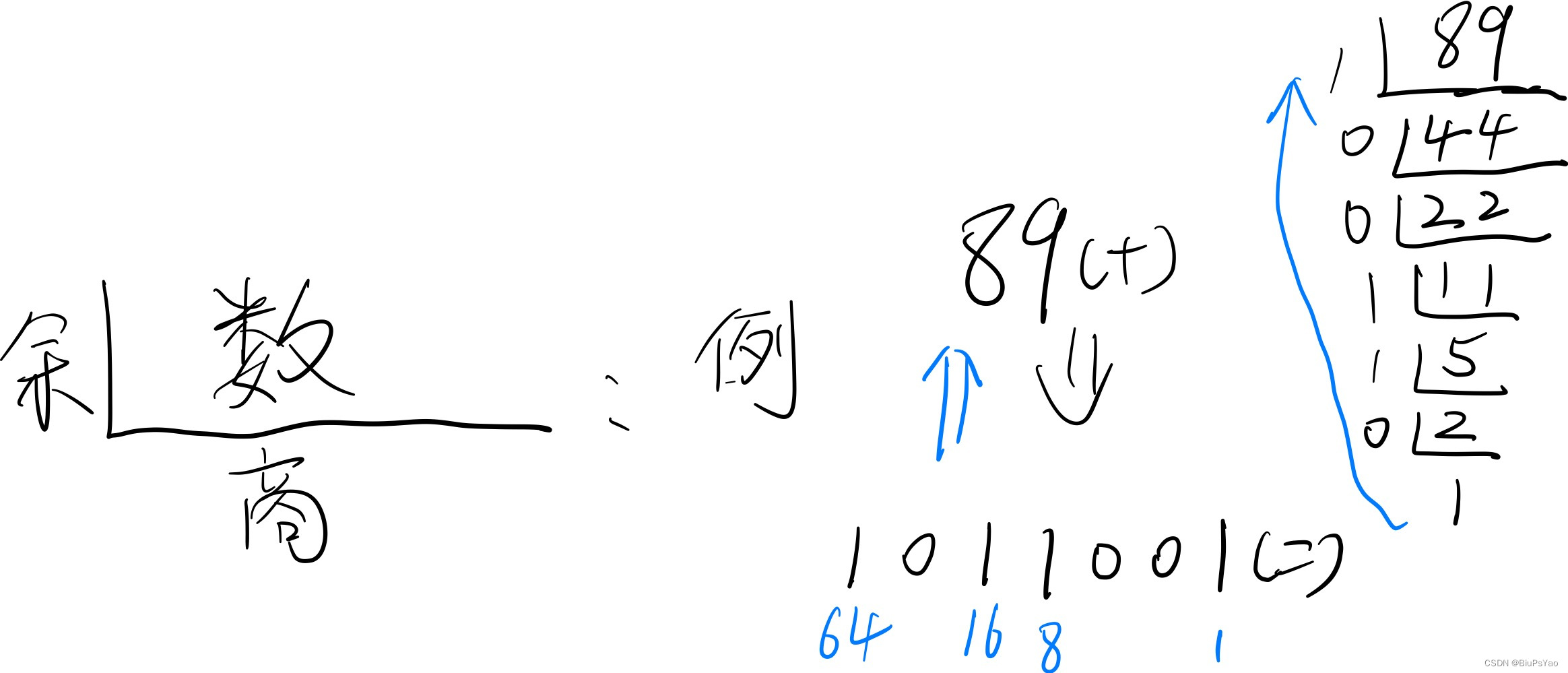






![[LK光流法,disflow using Dense Inverse Search, VariationalRefinement变分优化 原理和代码]](https://img-blog.csdnimg.cn/3ce77f38bf554b1699950beb8e7423fe.png)