文章目录
- 1.Fast Optical Flow using Dense Inverse Search
- 1.1 W的含义:
- 1.2 LK光流模型
- 1.3 LK光流模型求解(不含迭代)
- 1.4 LK光流模型迭代求解
- 1.5 dis_flow方法中的 LK光流模型
- 1.6 disflow代码分析
- 2.0 disflow中的VariationalRefinement方法
- 2.0 python调用code:
- 2.1 光流变分模型
- a. 灰度光流约束:
- b. 梯度光流约束
- c. 平滑约束
- d. 最终的约束方程:
- 2.2 优化求解
- 2.3 来看opencv的实现
- a. 接口类和实现类
- b. 具体实现介绍
- 3 线性方程组解法
- 4 变分法
- 5 参考文献
- 6 python 光流实验:
1.Fast Optical Flow using Dense Inverse Search
该篇论文是求dense flow,效果和速度都很好,虽然有源码(opencv上也有),但是网上的介绍不是很多,不是很容易理解。
要想理解该论文,首先要理解光流法
1.1 W的含义:
对于光流来说 W 表示光流:x方向上的光流u,y方向上的光流v
同时W也可以表示更复杂的坐标变换方法,比如affine仿射变换

1.2 LK光流模型
对图像2进行warp 与 图像1相减。
利用迭代的方法更新和优化


1.3 LK光流模型求解(不含迭代)




1.4 LK光流模型迭代求解
在4.2中提到迭代求解的光流模型
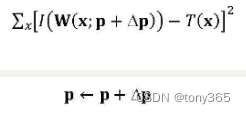
I 0 ( x , y ) = I 1 ( x + u , y + v ) I0(x,y) = I1(x+u, y+v) I0(x,y)=I1(x+u,y+v)变为 I 0 ( x , y ) = I 1 ( x + u + d u , y + v + d v ) I0(x,y) = I1(x+u+du, y+v+dv) I0(x,y)=I1(x+u+du,y+v+dv)
优化目标为:
m
i
n
∣
∣
I
0
(
x
,
y
)
−
I
1
(
x
+
u
+
d
u
,
y
+
v
+
d
v
)
∣
∣
2
min ||I0(x,y)-I1(x+u+du, y+v+dv)||^2
min∣∣I0(x,y)−I1(x+u+du,y+v+dv)∣∣2
令
I
0
(
x
,
y
)
−
I
1
(
x
+
u
+
d
u
,
y
+
v
+
d
v
)
=
0
I0(x,y)-I1(x+u+du, y+v+dv) = 0
I0(x,y)−I1(x+u+du,y+v+dv)=0
I
1
(
x
+
u
+
d
u
,
y
+
v
+
d
v
)
=
I
1
(
x
+
u
,
y
+
v
)
+
I
1
(
x
+
u
,
y
+
v
)
x
d
u
+
I
1
(
x
+
u
,
y
+
v
)
y
d
v
I1(x+u+du, y+v+dv) = I1(x+u, y+v) + I1(x+u, y+v)_x du + I1(x+u, y+v)_y dv
I1(x+u+du,y+v+dv)=I1(x+u,y+v)+I1(x+u,y+v)xdu+I1(x+u,y+v)ydv
令
I
1
w
a
r
p
=
I
1
(
x
+
u
,
y
+
v
)
I1warp = I1(x+u, y+v)
I1warp=I1(x+u,y+v)
已知上一次迭代u,v光流,或者初始设为0,可以求出
I
1
w
a
r
p
I1warp
I1warp
则
I
1
(
x
+
u
+
d
u
,
y
+
v
+
d
v
)
=
I
1
w
a
r
p
+
I
1
w
a
r
p
x
d
u
+
I
1
w
a
r
p
y
d
v
I1(x+u+du, y+v+dv) = I1warp + I1warp_x du + I1warp_y dv
I1(x+u+du,y+v+dv)=I1warp+I1warpxdu+I1warpydv
然后:
I
0
(
x
,
y
)
−
I
1
(
x
+
u
+
d
u
,
y
+
v
+
d
v
)
=
0
I
0
(
x
,
y
)
−
I
1
w
a
r
p
+
I
1
w
a
r
p
x
d
u
+
I
1
w
a
r
p
y
d
v
=
0
I
1
w
a
r
p
x
d
u
+
I
1
w
a
r
p
y
d
v
=
I
0
(
x
,
y
)
−
I
1
w
a
r
p
I
1
w
a
r
p
x
d
u
+
I
1
w
a
r
p
y
d
v
=
I
z
I0(x,y)-I1(x+u+du, y+v+dv)=0 \\ I0(x,y) - I1warp + I1warp_x du + I1warp_y dv =0\\ I1warp_x du + I1warp_y dv = I0(x,y) - I1warp\\ I1warp_x du + I1warp_y dv = Iz
I0(x,y)−I1(x+u+du,y+v+dv)=0I0(x,y)−I1warp+I1warpxdu+I1warpydv=0I1warpxdu+I1warpydv=I0(x,y)−I1warpI1warpxdu+I1warpydv=Iz
假设对于一个patchsize = 8邻域内的点, du, dv是相同的
则可以建立线性方程组,然后同4.3可通过最小二乘法求得
d
u
,
d
v
du, dv
du,dv
I
1
w
a
r
p
x
(
p
1
)
d
u
+
I
1
w
a
r
p
y
(
p
1
)
d
v
=
I
z
(
p
1
)
I
1
w
a
r
p
x
(
p
2
)
d
u
+
I
1
w
a
r
p
y
(
p
2
)
d
v
=
I
z
(
p
2
)
I
1
w
a
r
p
x
(
p
2
)
d
u
+
I
1
w
a
r
p
y
(
p
2
)
d
v
=
I
z
(
p
2
)
.
.
.
I
1
w
a
r
p
x
(
p
64
)
d
u
+
I
1
w
a
r
p
y
(
p
64
)
d
v
=
I
z
(
p
64
)
I1warp_x(p1) du + I1warp_y(p1) dv = Iz(p1)\\ I1warp_x(p2) du + I1warp_y(p2) dv = Iz(p2)\\ I1warp_x(p2) du + I1warp_y(p2) dv = Iz(p2)\\ ...\\ I1warp_x(p64) du + I1warp_y(p64) dv = Iz(p64)
I1warpx(p1)du+I1warpy(p1)dv=Iz(p1)I1warpx(p2)du+I1warpy(p2)dv=Iz(p2)I1warpx(p2)du+I1warpy(p2)dv=Iz(p2)...I1warpx(p64)du+I1warpy(p64)dv=Iz(p64)
可建立
A
d
=
b
Ad=b
Ad=b
其中
A
=
[
I
1
w
a
r
p
x
(
p
1
)
I
1
w
a
r
p
y
(
p
1
)
I
1
w
a
r
p
x
(
p
2
)
I
1
w
a
r
p
y
(
p
2
)
.
.
.
I
1
w
a
r
p
x
(
p
n
)
I
1
w
a
r
p
y
(
p
n
)
]
A=\left[ \begin{array}{ccc} I1warp_x(p1) \qquad I1warp_y(p1)\\ I1warp_x(p2) \qquad I1warp_y(p2)\\ ...\\ I1warp_x(pn) \qquad I1warp_y(pn)\\ \end{array} \right ]
A=
I1warpx(p1)I1warpy(p1)I1warpx(p2)I1warpy(p2)...I1warpx(pn)I1warpy(pn)
d
=
[
d
u
d
v
]
d=\left[ \begin{array}{ccc} du\\ dv \end{array} \right ]
d=[dudv]
b = [ I z ( p 1 ) I z ( p 2 ) . . . I z ( p n ) ] b=\left[ \begin{array}{ccc} Iz(p1)\\ Iz(p2)\\ ...\\ Iz(pn) \end{array} \right ] b= Iz(p1)Iz(p2)...Iz(pn)
最小二乘法
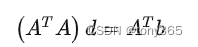
H
=
[
∑
I
1
w
a
r
p
x
×
I
1
w
a
r
p
x
∑
I
1
w
a
r
p
x
×
I
1
w
a
r
p
y
∑
I
1
w
a
r
p
x
×
I
1
w
a
r
p
y
∑
I
1
w
a
r
p
y
×
I
1
w
a
r
p
y
]
H=\left[ \begin{array}{ccc} \sum I1warp_x\times I1warp_x & \sum I1warp_x\times I1warp_y\\ \sum I1warp_x\times I1warp_y & \sum I1warp_y\times I1warp_y\\ \end{array} \right ]
H=[∑I1warpx×I1warpx∑I1warpx×I1warpy∑I1warpx×I1warpy∑I1warpy×I1warpy]
B
=
A
T
b
=
[
∑
I
1
w
a
r
p
x
I
z
∑
I
1
w
a
r
p
y
I
z
]
B=A^Tb = \left[ \begin{array}{ccc} \sum I1warp_x Iz\\ \sum I1warp_y Iz \end{array} \right ]
B=ATb=[∑I1warpxIz∑I1warpyIz]
d
=
H
−
1
×
B
d = H^{-1} \times B
d=H−1×B
最后更新
u
=
u
+
d
u
v
=
v
+
d
v
u = u+du\\ v=v+dv
u=u+duv=v+dv
以及 I1warp也要更新
1.5 dis_flow方法中的 LK光流模型
在4.4中,每次求出du,dv后首先更新u,v,然后更新I1warp
还要根据I1warp更新方程组的参数
I
1
w
a
r
p
x
,
I
1
w
a
r
p
y
I1warp_x ,I1warp_y
I1warpx,I1warpy
等于说是每次迭代都要重新算梯度。
而dis_flow方法采用下面的模型:
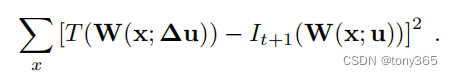
即每次求出 du, dv之后,并不是作用在 I1warp中,而是作用在 I0 中,当然光流也是相反的方向
I
0
(
x
+
d
u
,
y
+
d
v
)
−
I
1
(
x
+
u
,
y
+
v
)
=
0
I
0
(
x
,
y
)
+
I
0
x
d
u
+
I
0
y
d
v
−
I
1
(
x
+
u
,
y
+
v
)
=
0
I0(x+du, y+dv)-I1(x+u,y+v)=0\\ I0(x,y)+I0_xdu+I0_ydv-I1(x+u,y+v)=0
I0(x+du,y+dv)−I1(x+u,y+v)=0I0(x,y)+I0xdu+I0ydv−I1(x+u,y+v)=0
可以得到
I
0
x
d
u
+
I
0
y
d
v
=
I
1
(
x
+
u
,
y
+
v
)
−
I
0
(
x
,
y
)
I0_xdu + I0_ydv = I1(x+u,y+v)-I0(x,y)
I0xdu+I0ydv=I1(x+u,y+v)−I0(x,y)
同理可以求得 H 和 b,进而求出 du, dv
H
=
[
∑
I
0
x
×
I
0
x
∑
I
0
x
×
I
0
y
∑
I
0
x
×
I
0
y
∑
I
0
y
×
I
0
y
]
H=\left[ \begin{array}{ccc} \sum I0_x\times I0_x & \sum I0_x\times I0_y\\ \sum I0_x\times I0_y & \sum I0_y\times I0_y\\ \end{array} \right ]
H=[∑I0x×I0x∑I0x×I0y∑I0x×I0y∑I0y×I0y]
B
=
A
T
b
=
[
∑
I
0
x
I
z
∑
I
0
y
I
z
]
B=A^Tb = \left[ \begin{array}{ccc} \sum I0_x Iz\\ \sum I0_y Iz \end{array} \right ]
B=ATb=[∑I0xIz∑I0yIz]
d
=
H
−
1
×
B
d = H^{-1} \times B
d=H−1×B
更新
u
=
u
−
d
u
,
v
=
v
−
d
v
u=u-du, v=v-dv
u=u−du,v=v−dv 记住这里是相减,因为du,dv是对I0而言的,作用在I1上符号变号
更新
I
1
(
x
+
u
,
y
+
v
)
I1(x+u,y+v)
I1(x+u,y+v)
然后再次循环求解,H矩阵是由I0的梯度求的,而不是I1warp的梯度求得,因此不需要每次迭代更新,只需更新一次,大大减少计算量。
加入以上是针对一个小patch优化求解 u,v, 可以设置步长便利整个图像,得到每个patch的u,v如果patch有重叠,则加权平均。
最终得到每个像素点光流u,v
1.6 disflow代码分析
看代码的确实是这样:
1)computeSSD 函数计算 两个patch的ssd,
2)computeSSDMeanNorm 返回的 是 两个patch减去各自均值后的 SSD, 避免亮度差异对ssd的影响
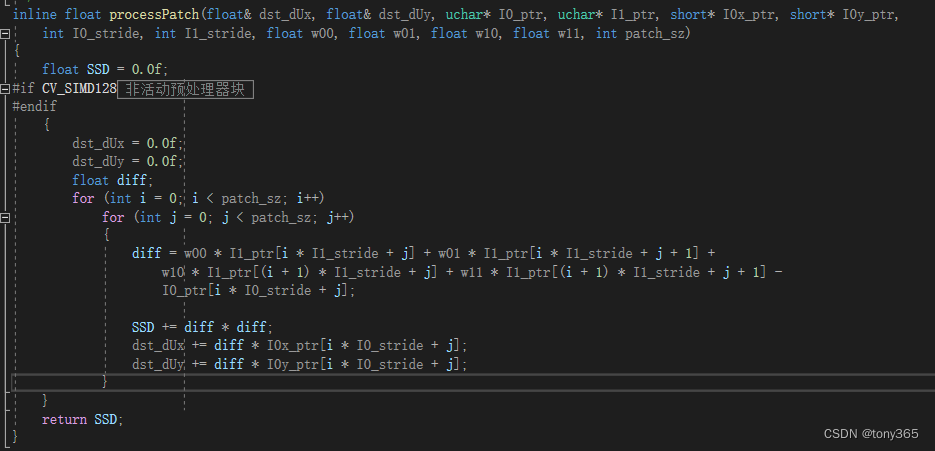
3)processPatch 函数 计算两个patch的ssd, 且 计算 dst_dUx, dst_dUy
对应的是
B
=
A
T
b
=
[
∑
I
0
x
I
z
∑
I
0
y
I
z
]
B=A^Tb = \left[ \begin{array}{ccc} \sum I0_x Iz\\ \sum I0_y Iz \end{array} \right ]
B=ATb=[∑I0xIz∑I0yIz]
diff对应的是
I
1
w
a
r
p
−
I
0
I1warp - I0
I1warp−I0
4)processPatchMeanNorm 函数是先均值归一化,在计算。
5)precomputeStructureTensor函数计算好每个patch的 地图平方和
对应的是H中的元素
H
=
[
∑
I
0
x
×
I
0
x
∑
I
0
x
×
I
0
y
∑
I
0
x
×
I
0
y
∑
I
0
y
×
I
0
y
]
H=\left[ \begin{array}{ccc} \sum I0_x\times I0_x & \sum I0_x\times I0_y\\ \sum I0_x\times I0_y & \sum I0_y\times I0_y\\ \end{array} \right ]
H=[∑I0x×I0x∑I0x×I0y∑I0x×I0y∑I0y×I0y]
Mat_<float> I0xx_buf; //!< sum of squares of x gradient values
Mat_<float> I0yy_buf; //!< sum of squares of y gradient values
Mat_<float> I0xy_buf; //!< sum of x and y gradient products
/* Extra buffers that are useful if patch mean-normalization is used: */
Mat_<float> I0x_buf; //!< sum of x gradient values
Mat_<float> I0y_buf; //!< sum of y gradient values
6) void DISOpticalFlowImpl::PatchInverseSearch_ParBody::operator()(const Range &range) const
函数中有每个patch的迭代过程:
计算 H − 1 H^{-1} H−1
/* Precomputed structure tensor */
float *xx_ptr = dis->I0xx_buf.ptr<float>();
float *yy_ptr = dis->I0yy_buf.ptr<float>();
float *xy_ptr = dis->I0xy_buf.ptr<float>();
/* And extra buffers for mean-normalization: */
float *x_ptr = dis->I0x_buf.ptr<float>();
float *y_ptr = dis->I0y_buf.ptr<float>();
/* Use the best candidate as a starting point for the gradient descent: */
float cur_Ux = Sx_ptr[is * dis->ws + js];
float cur_Uy = Sy_ptr[is * dis->ws + js];
/* Computing the inverse of the structure tensor: */
float detH = xx_ptr[is * dis->ws + js] * yy_ptr[is * dis->ws + js] -
xy_ptr[is * dis->ws + js] * xy_ptr[is * dis->ws + js];
if (abs(detH) < EPS)
detH = EPS;
float invH11 = yy_ptr[is * dis->ws + js] / detH;
float invH12 = -xy_ptr[is * dis->ws + js] / detH;
float invH22 = xx_ptr[is * dis->ws + js] / detH;
计算 dUx, dUy, 就是
B
=
A
T
b
=
[
∑
I
0
x
I
z
∑
I
0
y
I
z
]
B=A^Tb = \left[ \begin{array}{ccc} \sum I0_x Iz\\ \sum I0_y Iz \end{array} \right ]
B=ATb=[∑I0xIz∑I0yIz]
if (dis->use_mean_normalization)
SSD = processPatchMeanNorm(dUx, dUy,
I0_ptr + i * dis->w + j, I1_ptr + (int)i_I1 * w_ext + (int)j_I1,
I0x_ptr + i * dis->w + j, I0y_ptr + i * dis->w + j,
dis->w, w_ext, w00, w01, w10, w11, psz,
x_grad_sum, y_grad_sum);
else
SSD = processPatch(dUx, dUy,
I0_ptr + i * dis->w + j, I1_ptr + (int)i_I1 * w_ext + (int)j_I1,
I0x_ptr + i * dis->w + j, I0y_ptr + i * dis->w + j,
dis->w, w_ext, w00, w01, w10, w11, psz);
H
−
1
H^{-1}
H−1 和
B
B
B都算出来了
d
=
H
−
1
×
B
d = H^{-1} \times B
d=H−1×B
即
dx = invH11 * dUx + invH12 * dUy;
dy = invH12 * dUx + invH22 * dUy;
更新I1的u,v, 注意是相减,因为du,dv是作用在I0上的。
cur_Ux -= dx;
cur_Uy -= dy;
/* If gradient descent converged to a flow vector that is very far from the initial approximation
* (more than patch size) then we don't use it. Noticeably improves the robustness.
*/
//验证光流的范围变化不能超过patch_size
if (norm(Vec2f(cur_Ux - Sx_ptr[is * dis->ws + js], cur_Uy - Sy_ptr[is * dis->ws + js])) <= psz)
{
Sx_ptr[is * dis->ws + js] = cur_Ux;
Sy_ptr[is * dis->ws + js] = cur_Uy;
}
可以发现和咱们的公式推导完全一致。
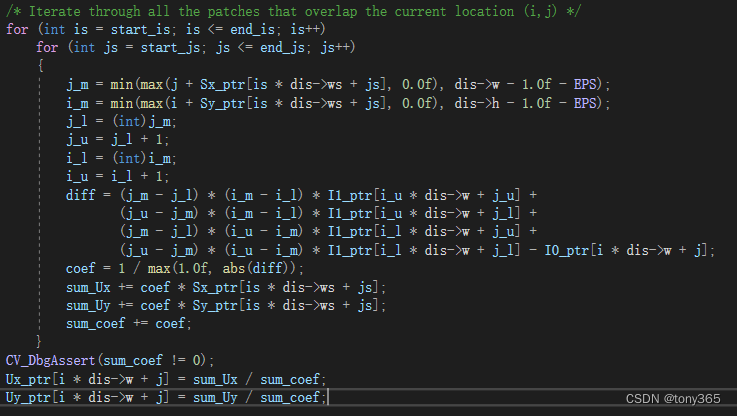
7) Densification_ParBody: patch flow fusion
在论文中有介绍融合方法:

以上求得是每个patch的光流,由于patch间隔不同存在overlap的时候,就加权平均得到某个像素的flow。
就是说该像素点 被多少个patch覆盖了,就求出多少个weight,这里Us表示.weight计算根据 I1warp(p)和I0(p)的差异得到。
差异越小说明warp更可能是对的,则weight更大。
最后加权融合得到该像素点的 u和v
void DISOpticalFlowImpl::Densification_ParBody::operator()(const Range &range) const
和文中公式一致
8)最后利用变分优化方法优化u, v
if (variational_refinement_iter > 0)
variational_refinement_processors[i]->calcUV(I0s[i], I1s[i], Ux[i], Uy[i]);
关于variational_refinement优化原理查看下一章节。
2.0 disflow中的VariationalRefinement方法
2.0 python调用code:
algo_var_refine = cv2.VariationalRefinement_create()
algo_var_refine.calcUV(im1, im2, flow_pca[..., 0].astype(np.float32), flow_pca[..., 1].astype(np.float32))
flow_var_refine = flow_pca
这是一个全局优化光流的方法,在disflow 和 deepflow中都有使用。
主要原理来自于两篇论文
论文1:High Accuracy Optical Flow Estimation Based on a
Theory for Warping[2004]
和
论文2:Beyond Pixels: Exploring New Representations and
Applications for Motion Analysis中的 A和B章节
2.1 光流变分模型
a. 灰度光流约束:
I ( x , y , t ) = I ( x + u , y + v , t + 1 ) I(x, y, t)=I(x+u,y+v,t+1) I(x,y,t)=I(x+u,y+v,t+1) (1)
上面公式的线性版本如下,但是下面等式成立的条件是运动是线性的:
I x u + I y u + I t = 0 I_xu+I_yu+I_t=0 Ixu+Iyu+It=0 (2)
b. 梯度光流约束
灰度可能容易受到图像亮度变化的影响,梯度会有更好的鲁棒性,因此引入梯度光流约束
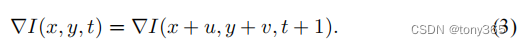
最终的data项约束为:

其中
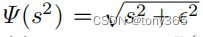
为什么用公式(5)而不是公式公式(4)?
原因是quadratic penalisers 容易收到outlier的影响
这也是二范数和一范数的区别。深度学习的损失函数也是同样的道理,如果想要损失都较小用平方L2; L1作为损失函数容易使部分sample loss=0,部分loss比较大,不受outlier的影响
c. 平滑约束
包含时域平滑和空域平滑,如果只有前后两帧则只包括空域平滑, 公式如下:
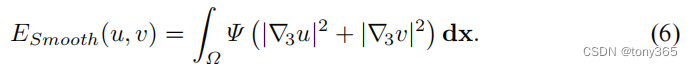
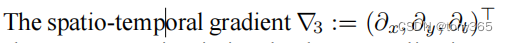
表示的x方向,y方向,时间t方向的偏微分(梯度),如果只有两张图像,就只剩下x方向和y方向。(最少3张图才能构成两张 时域上的梯度图,才能建立约束。)
d. 最终的约束方程:
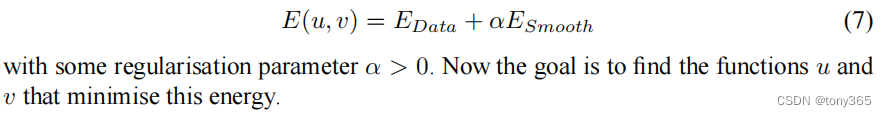
约束方程是关于两个函数u(x,y), v(x,y)的泛函。
在论文1中利用变分法求解, 转化为欧拉-拉格朗日方程后,利用fixed point iteration
loop 求解,论文1和2分别采用变分法和IterativeReweightedLeastSquare求解。因为opencv中的VariationalRefinement和论文2比较一致且论文2易懂,下面主要介绍论文2的求解方法。
2.2 优化求解
以下面的优化目标为例:
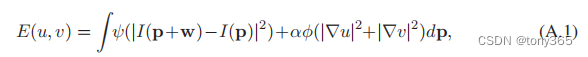
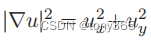
为什么选择下面的惩罚函数,原理已经说过,是为例避免outlier的影响。
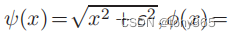
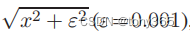
少了一个梯度项,不过优化原理是一样的。
在迭代框架下,可以改为:
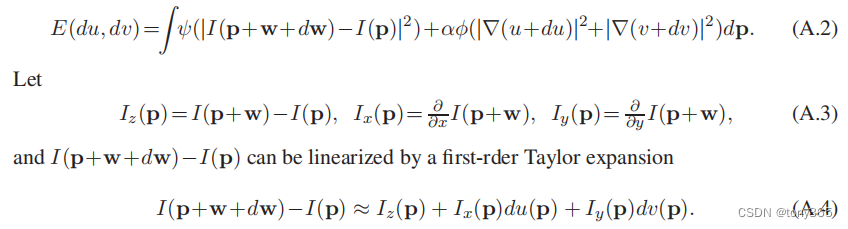
这里主要使用了一阶泰勒展开。
设
u
+
d
u
u+du
u+du在x和y方向上的梯度为
(
u
+
d
u
)
x
(u+du)_x
(u+du)x和
(
u
+
d
u
)
y
(u+du)_y
(u+du)y,等价与
D
x
=
[
−
1
,
0
,
1
]
Dx=[-1,0,1]
Dx=[−1,0,1]算子,
D
y
=
D
x
T
Dy=Dx^T
Dy=DxT算子
做卷积。
令
f
=
(
I
z
+
I
x
d
u
+
I
y
d
v
)
2
f=(I_z+I_xdu+I_ydv)^2
f=(Iz+Ixdu+Iydv)2
g
=
(
D
x
∗
(
u
+
d
u
)
)
2
+
(
D
y
∗
(
u
+
d
u
)
)
2
+
(
D
x
∗
(
v
+
d
v
)
)
2
+
(
D
y
∗
(
v
+
d
v
)
)
2
g=(Dx*(u+du))^2+(Dy*(u+du))^2+(Dx*(v+dv))^2+(Dy*(v+dv))^2
g=(Dx∗(u+du))2+(Dy∗(u+du))2+(Dx∗(v+dv))2+(Dy∗(v+dv))2
∗
*
∗号卷积,表示求偏导。
则可以得到:
E
(
d
u
,
d
v
)
=
∑
(
φ
(
f
)
+
α
ϕ
(
g
)
)
=
∑
(
φ
(
(
I
z
+
I
x
d
u
+
I
y
d
v
)
2
)
+
α
ϕ
(
(
D
x
∗
(
u
+
d
u
)
)
2
+
(
D
y
∗
(
u
+
d
u
)
)
2
+
(
D
x
∗
(
v
+
d
v
)
)
2
+
(
D
y
∗
(
v
+
d
v
)
)
2
)
)
E(du,dv)=\sum(\varphi(f) + \alpha\phi(g))\\ =\sum(\varphi((I_z+I_xdu+I_ydv)^2) + \alpha\phi((Dx*(u+du))^2+(Dy*(u+du))^2+(Dx*(v+dv))^2+(Dy*(v+dv))^2))
E(du,dv)=∑(φ(f)+αϕ(g))=∑(φ((Iz+Ixdu+Iydv)2)+αϕ((Dx∗(u+du))2+(Dy∗(u+du))2+(Dx∗(v+dv))2+(Dy∗(v+dv))2))
求和符合表示所有pixel.
iterative reweighted least squares (IRLS) 利用
gradient = 0求解 du, dv
∂
E
(
d
u
,
d
v
)
∂
d
u
=
0
\frac{\partial E(du,dv)}{\partial du}=0
∂du∂E(du,dv)=0
∂
E
(
d
u
,
d
v
)
∂
d
v
=
0
\frac{\partial E(du,dv)}{\partial dv}=0
∂dv∂E(du,dv)=0
∂
E
(
d
u
,
d
v
)
∂
d
u
=
∑
2
(
φ
′
(
f
)
(
I
z
+
I
x
d
u
+
I
y
d
v
)
I
x
+
α
ϕ
′
(
g
)
(
(
D
x
∗
(
u
+
d
u
)
∗
D
x
)
+
(
D
y
∗
(
u
+
d
u
)
∗
D
y
)
)
)
=
∑
2
(
φ
′
(
(
I
z
+
I
x
d
u
+
I
y
d
v
)
2
)
(
I
z
+
I
x
d
u
+
I
y
d
v
)
I
x
+
α
ϕ
′
(
g
)
(
(
D
x
∗
(
u
+
d
u
)
∗
D
x
)
+
(
D
x
∗
(
u
+
d
u
)
∗
D
x
)
)
)
=
∑
2
(
φ
′
(
(
I
z
+
I
x
d
u
+
I
y
d
v
)
2
)
(
I
z
+
I
x
d
u
+
I
y
d
v
)
I
x
+
α
(
(
D
x
D
x
∗
ϕ
′
(
g
)
+
(
D
y
D
y
∗
ϕ
′
(
g
)
)
(
u
+
d
u
)
)
\frac{\partial E(du,dv)}{\partial du}\\ =\sum2(\varphi'(f)(I_z+I_xdu+I_ydv)I_x + \alpha\phi'(g)((Dx*(u+du)*Dx)+(Dy*(u+du)*Dy)))\\ =\sum2(\varphi'((I_z+I_xdu+I_ydv)^2)(I_z+I_xdu+I_ydv)I_x + \alpha\phi'(g)((Dx*(u+du)*Dx)+(Dx*(u+du)*Dx)))\\ =\sum2(\varphi'((I_z+I_xdu+I_ydv)^2)(I_z+I_xdu+I_ydv)I_x + \alpha((DxDx*\phi'(g)+(DyDy*\phi'(g))(u+du))
∂du∂E(du,dv)=∑2(φ′(f)(Iz+Ixdu+Iydv)Ix+αϕ′(g)((Dx∗(u+du)∗Dx)+(Dy∗(u+du)∗Dy)))=∑2(φ′((Iz+Ixdu+Iydv)2)(Iz+Ixdu+Iydv)Ix+αϕ′(g)((Dx∗(u+du)∗Dx)+(Dx∗(u+du)∗Dx)))=∑2(φ′((Iz+Ixdu+Iydv)2)(Iz+Ixdu+Iydv)Ix+α((DxDx∗ϕ′(g)+(DyDy∗ϕ′(g))(u+du))
两个一阶导近似一个空间二阶导数 拉普拉斯算子

令 L = D x D x ∗ ϕ ′ ( g ) + D y D y ∗ ϕ ′ ( g ) L=DxDx*\phi'(g)+DyDy*\phi'(g) L=DxDx∗ϕ′(g)+DyDy∗ϕ′(g)
迭代计算的时候
f
f
f 也可以用warp后的图像 的平方表示,
因此首先初始化 du=dv=0,
然后计算
f
f
f和
g
g
g
然后计算
φ
′
(
f
)
\varphi'(f)
φ′(f),
ϕ
′
(
g
)
\phi'(g)
ϕ′(g), L
∂ E ( d u , d v ) ∂ d u = 2 ∑ ( φ ′ ( f ) I x 2 + α L ) d u + φ ′ ( f ) I x I y d v + φ ′ ( f ) I x I z + α L u \frac{\partial E(du,dv)}{\partial du}=2\sum{(\varphi'(f)I_x^2 + \alpha L) du + \varphi'(f)I_x I_y dv + \varphi'(f)I_x I_z + \alpha L u} ∂du∂E(du,dv)=2∑(φ′(f)Ix2+αL)du+φ′(f)IxIydv+φ′(f)IxIz+αLu
同理:
∂
E
(
d
u
,
d
v
)
∂
d
v
=
2
∑
(
φ
′
(
f
)
I
y
2
+
α
L
)
d
v
+
φ
′
(
f
)
I
x
I
y
d
u
+
φ
′
(
f
)
I
y
I
z
+
α
L
v
\frac{\partial E(du,dv)}{\partial dv}=2\sum{(\varphi'(f)I_y^2 + \alpha L) dv + \varphi'(f)I_x I_y du + \varphi'(f)I_y I_z + \alpha L v}
∂dv∂E(du,dv)=2∑(φ′(f)Iy2+αL)dv+φ′(f)IxIydu+φ′(f)IyIz+αLv
令 ∂ E ( d u , d v ) ∂ d u = 0 \frac{\partial E(du,dv)}{\partial du}=0 ∂du∂E(du,dv)=0和 ∂ E ( d u , d v ) ∂ d v = 0 \frac{\partial E(du,dv)}{\partial dv}=0 ∂dv∂E(du,dv)=0
得到:
Ax = b
其中
A=
[
(
φ
′
(
f
)
I
x
2
+
α
L
)
φ
′
(
f
)
I
x
I
y
φ
′
(
f
)
I
x
I
y
φ
′
(
f
)
I
y
2
+
α
L
)
]
\begin{bmatrix} (\varphi'(f)I_x^2 + \alpha L) & \varphi'(f)I_x I_y \\ \varphi'(f)I_x I_y & \varphi'(f)I_y^2 + \alpha L) \end{bmatrix}
[(φ′(f)Ix2+αL)φ′(f)IxIyφ′(f)IxIyφ′(f)Iy2+αL)]
x = [ d u d v ] \begin{bmatrix} du \\ dv \end{bmatrix} [dudv]
b= − [ φ ′ ( f ) I x I z + α L u φ ′ ( f ) I y I z + α L v ] -\begin{bmatrix} \varphi'(f)I_x I_z + \alpha L u \\ \varphi'(f)I_y I_z + \alpha L v \end{bmatrix} −[φ′(f)IxIz+αLuφ′(f)IyIz+αLv]
因此每次迭代求解du,dv。
2.3 来看opencv的实现
主要公式就是上面的Ax = b
a. 接口类和实现类
首先接口
#include "opencv2/opencv.hpp"
using namespace std;
using namespace cv;
/** @brief Variational optical flow refinement
This class implements variational refinement of the input flow field, i.e.
it uses input flow to initialize the minimization of the following functional:
\f$E(U) = \int_{\Omega} \delta \Psi(E_I) + \gamma \Psi(E_G) + \alpha \Psi(E_S) \f$,
where \f$E_I,E_G,E_S\f$ are color constancy, gradient constancy and smoothness terms
respectively. \f$\Psi(s^2)=\sqrt{s^2+\epsilon^2}\f$ is a robust penalizer to limit the
influence of outliers. A complete formulation and a description of the minimization
procedure can be found in @cite Brox2004
*/
//主要函数就是calcUV
class VariationalRefinement
{
public:
/** @brief @ref calc function overload to handle separate horizontal (u) and vertical (v) flow components
(to avoid extra splits/merges) */
virtual void calcUV(InputArray I0, InputArray I1, InputOutputArray flow_u, InputOutputArray flow_v) = 0;
/** @brief Number of outer (fixed-point) iterations in the minimization procedure.
@see setFixedPointIterations */
virtual int getFixedPointIterations() const = 0;
/** @copybrief getFixedPointIterations @see getFixedPointIterations */
virtual void setFixedPointIterations(int val) = 0;
/** @brief Number of inner successive over-relaxation (SOR) iterations
in the minimization procedure to solve the respective linear system.
@see setSorIterations */
virtual int getSorIterations() const = 0;
/** @copybrief getSorIterations @see getSorIterations */
virtual void setSorIterations(int val) = 0;
/** @brief Relaxation factor in SOR
@see setOmega */
virtual float getOmega() const = 0;
/** @copybrief getOmega @see getOmega */
virtual void setOmega(float val) = 0;
/** @brief Weight of the smoothness term
@see setAlpha */
virtual float getAlpha() const = 0;
/** @copybrief getAlpha @see getAlpha */
virtual void setAlpha(float val) = 0;
/** @brief Weight of the color constancy term
@see setDelta */
virtual float getDelta() const = 0;
/** @copybrief getDelta @see getDelta */
virtual void setDelta(float val) = 0;
/** @brief Weight of the gradient constancy term
@see setGamma */
virtual float getGamma() const = 0;
/** @copybrief getGamma @see getGamma */
virtual void setGamma(float val) = 0;
/** @brief Creates an instance of VariationalRefinement
*/
static Ptr<VariationalRefinement> create();
};
实现类:
class VariationalRefinementImpl
{
public:
VariationalRefinementImpl();
void calc(InputArray I0, InputArray I1, InputOutputArray flow) ;
void calcUV(InputArray I0, InputArray I1, InputOutputArray flow_u, InputOutputArray flow_v) ;
void collectGarbage() ;
protected: //!< algorithm parameters
int fixedPointIterations, sorIterations;
float omega;
float alpha, delta, gamma;
float zeta, epsilon;
public:
int getFixedPointIterations() const { return fixedPointIterations; }
void setFixedPointIterations(int val) { fixedPointIterations = val; }
int getSorIterations() const { return sorIterations; }
void setSorIterations(int val) { sorIterations = val; }
float getOmega() const { return omega; }
void setOmega(float val) { omega = val; }
float getAlpha() const { return alpha; }
void setAlpha(float val) { alpha = val; }
float getDelta() const { return delta; }
void setDelta(float val) { delta = val; }
float getGamma() const { return gamma; }
void setGamma(float val) { gamma = val; }
protected: //!< internal buffers
/* This struct defines a special data layout for Mat_<float>. Original buffer is split into two: one for "red"
* elements (sum of indices is even) and one for "black" (sum of indices is odd) in a checkerboard pattern. It
* allows for more efficient processing in SOR iterations, more natural SIMD vectorization and parallelization
* (Red-Black SOR). Additionally, it simplifies border handling by adding repeated borders to both red and
* black buffers.
*/
struct RedBlackBuffer
{
Mat_<float> red; //!< (i+j)%2==0
Mat_<float> black; //!< (i+j)%2==1
/* Width of even and odd rows may be different */
int red_even_len, red_odd_len;
int black_even_len, black_odd_len;
RedBlackBuffer();
void create(Size s);
void release();
};
Mat_<float> Ix, Iy, Iz, Ixx, Ixy, Iyy, Ixz, Iyz; //!< image derivative buffers
RedBlackBuffer Ix_rb, Iy_rb, Iz_rb, Ixx_rb, Ixy_rb, Iyy_rb, Ixz_rb, Iyz_rb; //!< corresponding red-black buffers
RedBlackBuffer A11, A12, A22, b1, b2; //!< main linear system coefficients
RedBlackBuffer weights; //!< smoothness term weights in the current fixed point iteration
Mat_<float> mapX, mapY; //!< auxiliary buffers for remapping
RedBlackBuffer tempW_u, tempW_v; //!< flow buffers that are modified in each fixed point iteration
RedBlackBuffer dW_u, dW_v; //!< optical flow increment
RedBlackBuffer W_u_rb, W_v_rb; //!< red-black-buffer version of the input flow
private: //!< private methods and parallel sections
void splitCheckerboard(RedBlackBuffer& dst, Mat& src);
void mergeCheckerboard(Mat& dst, RedBlackBuffer& src);
void updateRepeatedBorders(RedBlackBuffer& dst);
void warpImage(Mat& dst, Mat& src, Mat& flow_u, Mat& flow_v);
void prepareBuffers(Mat& I0, Mat& I1, Mat& W_u, Mat& W_v);
/* Parallelizing arbitrary operations with 3 input/output arguments */
typedef void (VariationalRefinementImpl::* Op)(void* op1, void* op2, void* op3);
struct ParallelOp_ParBody : public ParallelLoopBody
{
VariationalRefinementImpl* var;
vector<Op> ops;
vector<void*> op1s;
vector<void*> op2s;
vector<void*> op3s;
ParallelOp_ParBody(VariationalRefinementImpl& _var, vector<Op> _ops, vector<void*>& _op1s,
vector<void*>& _op2s, vector<void*>& _op3s);
void operator()(const Range& range) const ;
};
void gradHorizAndSplitOp(void* src, void* dst, void* dst_split)
{
Sobel(*(Mat*)src, *(Mat*)dst, -1, 1, 0, 1, 1, 0.00, BORDER_REPLICATE);
splitCheckerboard(*(RedBlackBuffer*)dst_split, *(Mat*)dst);
}
void gradVertAndSplitOp(void* src, void* dst, void* dst_split)
{
Sobel(*(Mat*)src, *(Mat*)dst, -1, 0, 1, 1, 1, 0.00, BORDER_REPLICATE);
splitCheckerboard(*(RedBlackBuffer*)dst_split, *(Mat*)dst);
}
void averageOp(void* src1, void* src2, void* dst)
{
addWeighted(*(Mat*)src1, 0.5, *(Mat*)src2, 0.5, 0.0, *(Mat*)dst, CV_32F);
}
void subtractOp(void* src1, void* src2, void* dst)
{
subtract(*(Mat*)src1, *(Mat*)src2, *(Mat*)dst, noArray(), CV_32F);
}
struct ComputeDataTerm_ParBody : public ParallelLoopBody
{
VariationalRefinementImpl* var;
int nstripes, stripe_sz;
int h;
RedBlackBuffer* dW_u, * dW_v;
bool red_pass;
ComputeDataTerm_ParBody(VariationalRefinementImpl& _var, int _nstripes, int _h, RedBlackBuffer& _dW_u,
RedBlackBuffer& _dW_v, bool _red_pass);
void operator()(const Range& range) const ;
};
struct ComputeSmoothnessTermHorPass_ParBody : public ParallelLoopBody
{
VariationalRefinementImpl* var;
int nstripes, stripe_sz;
int h;
RedBlackBuffer* W_u, * W_v, * curW_u, * curW_v;
bool red_pass;
ComputeSmoothnessTermHorPass_ParBody(VariationalRefinementImpl& _var, int _nstripes, int _h,
RedBlackBuffer& _W_u, RedBlackBuffer& _W_v, RedBlackBuffer& _tempW_u,
RedBlackBuffer& _tempW_v, bool _red_pass);
void operator()(const Range& range) const ;
};
struct ComputeSmoothnessTermVertPass_ParBody : public ParallelLoopBody
{
VariationalRefinementImpl* var;
int nstripes, stripe_sz;
int h;
RedBlackBuffer* W_u, * W_v;
bool red_pass;
ComputeSmoothnessTermVertPass_ParBody(VariationalRefinementImpl& _var, int _nstripes, int _h,
RedBlackBuffer& W_u, RedBlackBuffer& _W_v, bool _red_pass);
void operator()(const Range& range) const ;
};
struct RedBlackSOR_ParBody : public ParallelLoopBody
{
VariationalRefinementImpl* var;
int nstripes, stripe_sz;
int h;
RedBlackBuffer* dW_u, * dW_v;
bool red_pass;
RedBlackSOR_ParBody(VariationalRefinementImpl& _var, int _nstripes, int _h, RedBlackBuffer& _dW_u,
RedBlackBuffer& _dW_v, bool _red_pass);
void operator()(const Range& range) const ;
};
};
b. 具体实现介绍
- 上面有一些struct 继承自ParallelLoopBody, 主要是tbb的优化方法并行加速操作
- calc函数: 比如输入为I0,I1两个图像,和一个光流flow, 然后主要调用calcUV函数
void VariationalRefinementImpl::calc(InputArray I0, InputArray I1, InputOutputArray flow)
{
CV_Assert(!I0.empty() && I0.channels() == 1);
CV_Assert(!I1.empty() && I1.channels() == 1);
CV_Assert(I0.sameSize(I1));
CV_Assert((I0.depth() == CV_8U && I1.depth() == CV_8U) || (I0.depth() == CV_32F && I1.depth() == CV_32F));
CV_Assert(!flow.empty() && flow.depth() == CV_32F && flow.channels() == 2);
CV_Assert(I0.sameSize(flow));
Mat uv[2];
Mat& flowMat = flow.getMatRef();
split(flowMat, uv);
calcUV(I0, I1, uv[0], uv[1]);
merge(uv, 2, flowMat);
}
- calcUV函数:也是整个算法的框架
void VariationalRefinementImpl::calcUV(InputArray I0, InputArray I1, InputOutputArray flow_u, InputOutputArray flow_v)
{
//一些assert操作, 对输入的要求
CV_Assert(!I0.empty() && I0.channels() == 1);
CV_Assert(!I1.empty() && I1.channels() == 1);
CV_Assert(I0.sameSize(I1));
CV_Assert((I0.depth() == CV_8U && I1.depth() == CV_8U) || (I0.depth() == CV_32F && I1.depth() == CV_32F));
CV_Assert(!flow_u.empty() && flow_u.depth() == CV_32F && flow_u.channels() == 1);
CV_Assert(!flow_v.empty() && flow_v.depth() == CV_32F && flow_v.channels() == 1);
CV_Assert(I0.sameSize(flow_u));
CV_Assert(flow_u.sameSize(flow_v));
int num_stripes = getNumThreads();//多线程相关,可以不做了解
Mat I0Mat = I0.getMat();
Mat I1Mat = I1.getMat();
Mat& W_u = flow_u.getMatRef();
Mat& W_v = flow_v.getMatRef();
prepareBuffers(I0Mat, I1Mat, W_u, W_v);
splitCheckerboard(W_u_rb, W_u);
splitCheckerboard(W_v_rb, W_v);
W_u_rb.red.copyTo(tempW_u.red);
W_u_rb.black.copyTo(tempW_u.black);
W_v_rb.red.copyTo(tempW_v.red);
W_v_rb.black.copyTo(tempW_v.black);
dW_u.red.setTo(0.0f);
dW_u.black.setTo(0.0f);
dW_v.red.setTo(0.0f);
dW_v.black.setTo(0.0f);
for (int i = 0; i < fixedPointIterations; i++)
{
//CV_TRACE_REGION("fixedPoint_iteration");
parallel_for_(Range(0, num_stripes), ComputeDataTerm_ParBody(*this, num_stripes, I0Mat.rows, dW_u, dW_v, true));
parallel_for_(Range(0, num_stripes), ComputeDataTerm_ParBody(*this, num_stripes, I0Mat.rows, dW_u, dW_v, false));
parallel_for_(Range(0, num_stripes), ComputeSmoothnessTermHorPass_ParBody(
*this, num_stripes, I0Mat.rows, W_u_rb, W_v_rb, tempW_u, tempW_v, true));
parallel_for_(Range(0, num_stripes), ComputeSmoothnessTermHorPass_ParBody(
*this, num_stripes, I0Mat.rows, W_u_rb, W_v_rb, tempW_u, tempW_v, false));
parallel_for_(Range(0, num_stripes),
ComputeSmoothnessTermVertPass_ParBody(*this, num_stripes, I0Mat.rows, W_u_rb, W_v_rb, true));
parallel_for_(Range(0, num_stripes),
ComputeSmoothnessTermVertPass_ParBody(*this, num_stripes, I0Mat.rows, W_u_rb, W_v_rb, false));
for (int j = 0; j < sorIterations; j++)
{
//CV_TRACE_REGION("SOR_iteration");
parallel_for_(Range(0, num_stripes), RedBlackSOR_ParBody(*this, num_stripes, I0Mat.rows, dW_u, dW_v, true));
parallel_for_(Range(0, num_stripes), RedBlackSOR_ParBody(*this, num_stripes, I0Mat.rows, dW_u, dW_v, false));
}
tempW_u.red = W_u_rb.red + dW_u.red;
tempW_u.black = W_u_rb.black + dW_u.black;
updateRepeatedBorders(tempW_u);
tempW_v.red = W_v_rb.red + dW_v.red;
tempW_v.black = W_v_rb.black + dW_v.black;
updateRepeatedBorders(tempW_v);
}
mergeCheckerboard(W_u, tempW_u);
mergeCheckerboard(W_v, tempW_v);
}
算法框架:

1)prepareBuffers函数中warp I1得到warpedI,然后让它与 I0 求个平均(这里只是增加鲁棒性), 对应I(p+w)
主要计算
a
v
e
r
a
g
e
d
I
=
I
0
∗
0.5
+
w
a
r
p
e
d
I
∗
0.5
对应公式中的
I
(
p
+
w
)
I
z
=
w
a
r
p
e
d
I
−
I
0
对应公式中的
I
z
I
x
I
y
I
x
z
I
y
z
I
x
x
I
y
y
I
x
y
都是字面意思
averagedI = I0*0.5 +warpedI*0.5 \qquad 对应公式中的 I(p+w)\\ Iz = warpedI - I0 \qquad 对应公式中的 Iz\\ Ix\\ Iy\\ Ixz\\ Iyz\\ Ixx\\ Iyy\\ Ixy \qquad 都是字面意思
averagedI=I0∗0.5+warpedI∗0.5对应公式中的I(p+w)Iz=warpedI−I0对应公式中的IzIxIyIxzIyzIxxIyyIxy都是字面意思
后缀 _rb 是把矩阵分成两个,主要是为了方便计算。
2)ComputeDataTerm_ParBody
weight 对应
φ
′
(
f
)
\varphi'(f)
φ′(f)
a11, a12, a22, b1,b2 都可以求出,当然这只是 gray 约束
/* Step 1: Compute color constancy terms */
/* Normalization factor:*/
derivNorm = pIx[j] * pIx[j] + pIy[j] * pIy[j] + zeta_squared;
/* Color constancy penalty (computed by Taylor expansion):*/
Ik1z = pIz[j] + pIx[j] * pdU[j] + pIy[j] * pdV[j];
/* Weight of the color constancy term in the current fixed-point iteration divided by derivNorm: */
weight = (delta2 / sqrt(Ik1z * Ik1z / derivNorm + epsilon_squared)) / derivNorm;
/* Add respective color constancy terms to the linear system coefficients: */
pa11[j] = weight * (pIx[j] * pIx[j]) + zeta_squared;
pa12[j] = weight * (pIx[j] * pIy[j]);
pa22[j] = weight * (pIy[j] * pIy[j]) + zeta_squared;
pb1[j] = -weight * (pIz[j] * pIx[j]);
pb2[j] = -weight * (pIz[j] * pIy[j]);
代码中同样计算了 gradiant 约束。
3)ComputeSmoothnessTermHorPass_ParBody 和 ComputeSmoothnessTermVertPass_ParBody
计算水平和竖直方向上的平滑约束
pWeight[j] = alpha2 / sqrt(ux * ux + vx * vx + uy * uy + vy * vy + epsilon_squared); 这里求 ϕ \phi ϕ的导数,对应 α ϕ ′ ( g ) \alpha \phi'(g) αϕ′(g)
经过以上步骤后得到 A 和 b,然后求x.
4) RedBlackSOR_ParBody
solve Ax = b
sigmaU = pW_next[j - 1] * pdu_next[j - 1] + pW[j] * pdu_next[j] + pW_prev_row[j] * pdu_prev_row[j] + pW[j] * pdu_next_row[j];
sigmaV = pW_next[j - 1] * pdv_next[j - 1] + pW[j] * pdv_next[j] + pW_prev_row[j] * pdv_prev_row[j] +pW[j] * pdv_next_row[j];
pdu[j] += var->omega * ((sigmaU + pb1[j] - pdv[j] * pa12[j]) / pa11[j] - pdu[j]);
pdv[j] += var->omega * ((sigmaV + pb2[j] - pdu[j] * pa12[j]) / pa22[j] - pdv[j]);
参考:
Large Displacement Optical Flow: Descriptor Matching in Variational Motion Estimation
对上面的方法进行优化,增加匹配项约束,意思就是加入我们检测数一些特征点匹配,这些匹配点可以得到 u,v, 增加约束。
图像处理中的全局优化技术(Global optimization techniques in image processing and computer vision) (三) 介绍了几篇 变分光流法论文
3 线性方程组解法
关于线性方程组的数值解法一般有两类:直接法和迭代法
- 直接法:直接法就是经过有限步算术运算,可求得线性方程组精确解的方法(若计算过程中没有舍入误差)。常用于求解低阶稠密矩阵方程组及某些大型稀疏矩阵方程组(如大型带状方程组)。
- 迭代法:迭代法就是用某种极限过程去逐步逼近线性方程组精确解的方法。优点:存储单元少、程序设计简单、原始系数矩阵在计算过程始终不变等;缺点:存在收敛性及收敛速度问题。常用于求解大型稀疏矩阵方程组(尤其是由微分方程离散后得到的大型方程组)。
直接法的介绍参考:第5章 解线性方程组的直接方法
迭代法参考:第6章 解线性方程组的迭代法(基于MATLAB)
解线性方程组的迭代法
数值分析】Jacobi、Seidel和Sor迭代法求解线性方程组(附matlab代码)
4 变分法
定义:泛函是以函数为变量的函数。即它的输入是函数,输出是实数。而这个输出值取决于一个或多个函数(输入)在一整个路径上的积分。
那么什么是变分法呢?求泛函极值的方法称为变分法。
变分法将泛函极值问题转换为一个非线性偏微分方程,又称为PDE,怎么求这个方程呢?
一般是转化为非线性代数方程组,然后迭代的方法求解,比如梯度下降。
应用在图像降噪和修复,dense flow estimation等。

变分法简介Part 1.(Calculus of Variations) 该系列有系统的介绍
浅谈变分原理
详细的示例
变分法初步:book
基于变分法的感知色彩校正 这是一个特别好的应用
5 参考文献
关于Lucas-Kanade 光流法原理:
-
Lucas-Kanade 20 Years On: A Unifying Framework 翻译(一)
讲解了1)光流法模型,2)warp方式, 3)inverse search方法。4)耗时
很有参考价值,比如
不同的warp方式的优化。不是optical flow这种直接相加的warp,而是仿射变换的参数化 warp, 也可以求出仿射变换的参数。只不过每个点都有自己的仿射参数。换句话说,加入两幅图像满足仿射变换关系,可以通过这个方法来求解变换关系,应用在前后帧的对齐上。
-
视觉SLAM十四讲作业练习(6) 光流法跟踪单点,有代码。
-
DIS 光流详解 对Fast Optical Flow using Dense Inverse Search论文的概述
关于DIS代码:
- of_dis
- Optical flow using dense inverse search
- opencv代码:opencv4以上版本 在 video/tracking 模块中, 还是opencv清晰易读一些
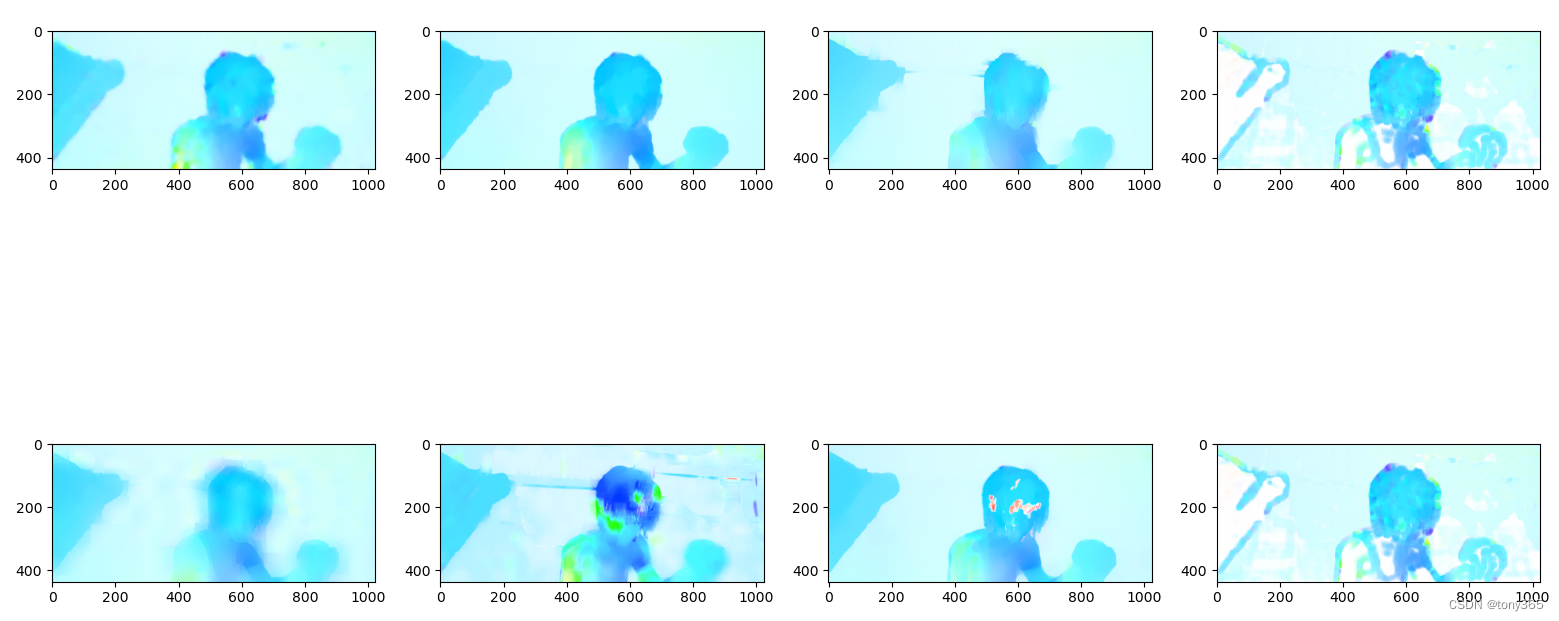
6 python 光流实验:
利用MPI-Sintel的一组图片,调用各种光流方法:
import os
import cv2
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import hsv_to_rgb
from torchvision.utils import flow_to_image
import torch
from show_flow import draw_flow
import time
def flow_to_image_torch(flow):
flow = torch.from_numpy(np.transpose(flow, [2, 0, 1]))
flow_im = flow_to_image(flow)
img = np.transpose(flow_im.numpy(), [1, 2, 0])
#print(img.shape)
return img
def show_flow_im(frame, flow):
h, w, c = frame.shape
flow_im3 = flow_to_image_torch(flow)
#print(h, w, c, min(h, w)//40)
flow_im4 = draw_flow(frame, flow, 20)
plt.figure()
plt.subplot(121)
plt.imshow(flow_im3)
plt.subplot(122)
plt.imshow(flow_im4)
plt.show()
def cal_flow(frame1, frame2):
"""
:param frame1: input image 1
:param frame2: input image 2
:return: optical flow
"""
im1 = cv2.cvtColor(frame1, cv2.COLOR_BGR2GRAY)
im2 = cv2.cvtColor(frame2, cv2.COLOR_BGR2GRAY)
algo_dis = cv2.DISOpticalFlow_create(cv2.DISOPTICAL_FLOW_PRESET_MEDIUM)
algo_dis.setUseSpatialPropagation(True)
flow = algo_dis.calc(im1, im2, None, )
return flow
def cal_flow_algos(frame1, frame2):
"""
:param frame1: input image 1
:param frame2: input image 2
:return: optical flow
"""
im1 = cv2.cvtColor(frame1, cv2.COLOR_BGR2GRAY)
im2 = cv2.cvtColor(frame2, cv2.COLOR_BGR2GRAY)
times = []
start = time.time()
algo_dis = cv2.DISOpticalFlow_create(cv2.DISOPTICAL_FLOW_PRESET_MEDIUM)
algo_dis.setUseSpatialPropagation(True)
flow_dis = algo_dis.calc(im1, im2, None, )
end = time.time()
times.append(end-start)
start = end
algo_deepflow = cv2.optflow.createOptFlow_DeepFlow()
flow_deepflow = algo_deepflow.calc(im1, im2, None)
end = time.time()
times.append(end-start)
start = end
flow_sparse = cv2.optflow.calcOpticalFlowSparseToDense(im1, im2)
end = time.time()
times.append(end - start)
start = end
flow_fb = cv2.calcOpticalFlowFarneback(im1, im2, None, 0.5, 3, 15, 3, 5, 1.2, 0)
end = time.time()
times.append(end - start)
start = end
algo_pca = cv2.optflow.createOptFlow_PCAFlow()
flow_pca = algo_pca.calc(im1, im2, None)
end = time.time()
times.append(end - start)
start = end
flow_simple = cv2.optflow.calcOpticalFlowSF(frame1, frame2, 1, 5, 5) # color image
end = time.time()
times.append(end - start)
start = end
flow_TVL1 = cv2.optflow.DualTVL1OpticalFlow_create()
flow_tvl1 = flow_TVL1.calc(im1, im2, None)
end = time.time()
times.append(end - start)
start = end
algo_var_refine = cv2.VariationalRefinement_create()
flow_var_refine = flow_fb
algo_var_refine.calcUV(im1, im2, flow_var_refine[..., 0].astype(np.float32), flow_var_refine[..., 1].astype(np.float32))
end = time.time()
times.append(end - start)
print(flow_var_refine.shape)
print('run time:', times)
return [flow_dis, flow_deepflow, flow_sparse, flow_fb, flow_pca, flow_simple, flow_tvl1, flow_var_refine]
def flow_warp(im1, im2, flow):
"""
:param im1: pre image
:param im2: next image
:param flow: optical flow ,im1 to im2
:return:
"""
h, w, c = im1.shape
hh = np.arange(0, h)
ww = np.arange(0, w)
xx, yy = np.meshgrid(ww, hh)
tx = xx - flow[..., 0]
ty = yy - flow[..., 1]
mask = ((tx < 0) + (ty < 0) + (tx > w - 1) + (ty > h - 1)) > 0
# print(mask.shape, mask.dtype, np.sum(mask))
# out = interp_linear(image, tx, ty)
# warped im1, should compare with im2
out = cv2.remap(im1, tx.astype(np.float32), ty.astype(np.float32), interpolation=cv2.INTER_LINEAR)
out[mask] = 0
return out
def cal_epe(flow_gt, flow):
diff = flow_gt - flow
return np.mean(np.sqrt((np.sum(diff*diff, axis=-1))))
def load_flow_to_numpy(path):
with open(path, 'rb') as f:
magic = np.fromfile(f, np.float32, count=1)
assert (202021.25 == magic), 'Magic number incorrect. Invalid .flo file'
w = np.fromfile(f, np.int32, count=1)[0]
h = np.fromfile(f, np.int32, count=1)[0]
data = np.fromfile(f, np.float32, count=2 * w * h)
data2D = np.reshape(data, (h, w, 2))
#print(data2D[:10,:10,0])
return data2D
if __name__ == "__main__":
print('cv2 version: {}'.format(cv2.__version__))
file1 = r'D:\codeflow\MPI-Sintel-complete\training\final\alley_1\frame_0001.png'
file2 = r'D:\codeflow\MPI-Sintel-complete\training\final\alley_1\frame_0002.png'
# 读取图片
frame1 = cv2.imread(file1)
h, w, c = frame1.shape
frame2 = cv2.imread(file2)
frame2 = cv2.resize(frame2, (w, h))
im1 = cv2.cvtColor(frame1, cv2.COLOR_BGR2GRAY)
im2 = cv2.cvtColor(frame2, cv2.COLOR_BGR2GRAY)
algo_names = ['flow_dis', 'flow_deepflow', 'flow_sparse', 'flow_fb', 'flow_pca', 'flow_simple', 'flow_tvl1', 'flow_var_refine']
# 计算光流
flows = cal_flow_algos(frame1, frame2)
# 读取flow gt
file_flow = r'D:\codeflow\MPI-Sintel-complete\training\flow\alley_1\frame_0001.flo'
flow_gt = load_flow_to_numpy(file_flow)
flow_gt_im = flow_to_image_torch(flow_gt)
# 计算epe
flow_gt = cv2.resize(flow_gt, (w, h))
epes = []
for flow in flows:
epe = cal_epe(flow_gt, flow)
epes.append(epe)
print(epes)
# 画出光流图
plt.figure()
num = len(flows)
col_num = (num + 1) // 2
for i in range(num):
print(flows[i].min(), flows[i].max(), flows[i].dtype, flows[i].shape)
flows[i][np.isnan(flows[i])] = 0
plt.subplot(2, col_num, i + 1)
flow_im = flow_to_image_torch(flows[i])
plt.imshow(flow_im)
# warp
im_warp = flow_warp(frame1, frame2, flows[i])
# cv2.imwrite(file1[:-4]+algo_names[i]+'.png', im_warp)
plt.show()