打卡第15天,今天继续二叉树
今日任务
- 层序遍历10道题
- 226.翻转二叉树
- 101.对称二叉树
层序遍历10道题
题单
- 102.二叉树的层序遍历
- 107.二叉树的层次遍历II
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
二叉树的层序遍历
就是从上到下,从左到右,一层层的遍历结点。
借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
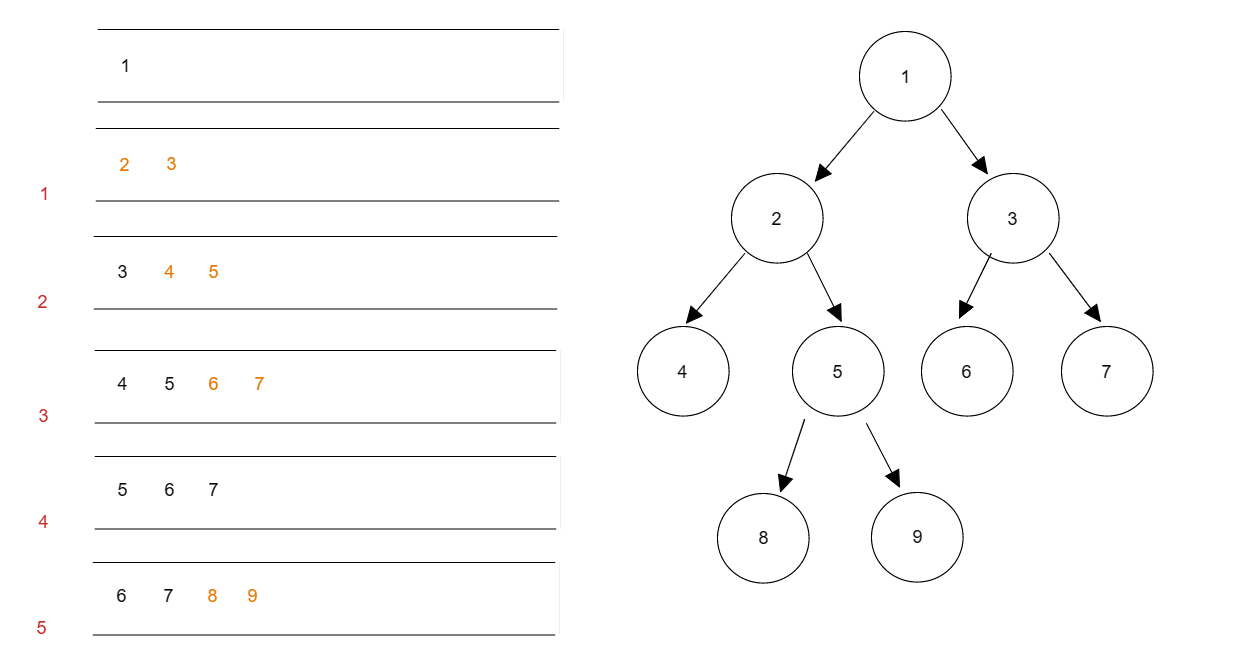
102.二叉树的层序遍历
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
if(root) que.push(root);
while(!que.empty()) {
int size = que.size();
vector<int> path;
while(size--) {
TreeNode *cur = que.front();
path.push_back(cur->val);
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
res.push_back(path);
}
return res;
}
};
为什么需要设置一个size,如果没有 size,我们无法知道队列的元素是属于当前层的,还是下一层的,添加了size取值为队列的长度,当size为0,说明当前层已经全部遍历,开始遍历下一层。
226.翻转二叉树
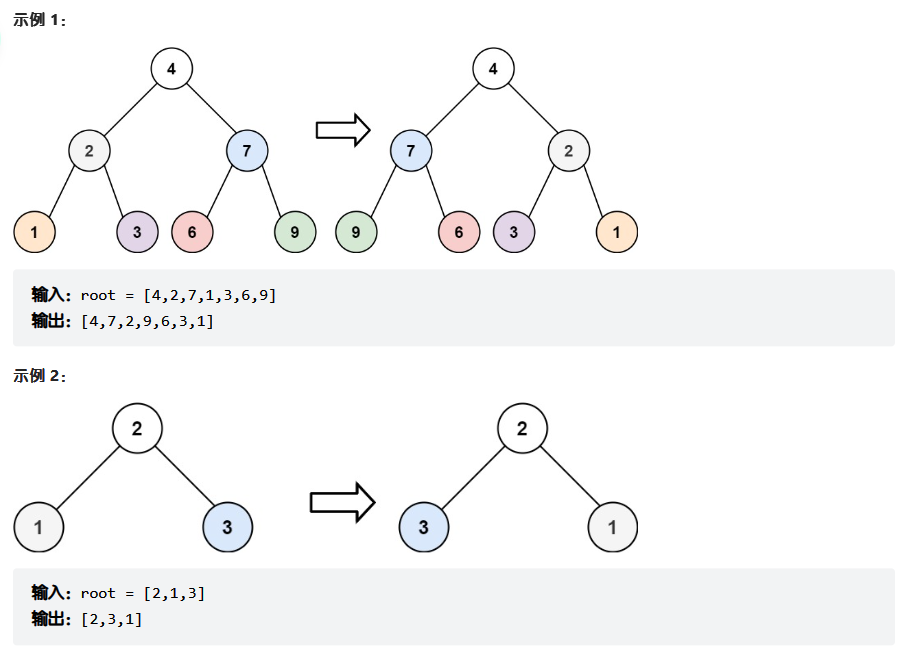
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
题解
翻转二叉树,需要把左右孩子全部翻转。
利用前序遍历,当访问到中间结点时候,翻转他的左右孩子,
前序(深度优先遍历)写法
迭代
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if(root) st.push(root);
while(!st.empty()) {
TreeNode* cur = st.top();
swap(cur->left, cur->right);
st.pop();
if(cur->left) st.push(cur->left);
if(cur->right) st.push(cur->right);
}
return root;
}
};
递归
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == NULL) return root;
invertTree(root->left);
invertTree(root->right);
swap(root->left, root->right);
return root;
}
};
层序(广度优先遍历)写法
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()) {
TreeNode* cur = que.front();
if(cur) swap(cur->left, cur->right);
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
return root;
}
};
101.对称二叉树
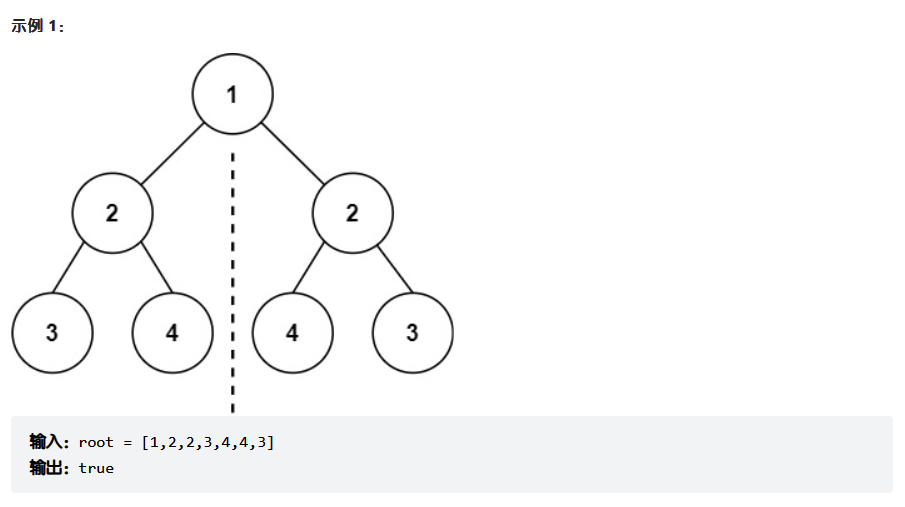
给你一个二叉树的根节点
root, 检查它是否轴对称。
代码随想录
判断对称二叉树要比较的是哪两个节点,要比较的不是左右节点,而是比较根结点的左右子树是不是可以相互对称,用递归遍历的时候,我们需要遍历的是两棵子树。
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// 首先排除空节点的情况
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// 排除了空节点,再排除数值不相同的情况
else if (left->val != right->val) return false;
// 此时就是:左右节点都不为空,且数值相同的情况
// 此时才做递归,做下一层的判断
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
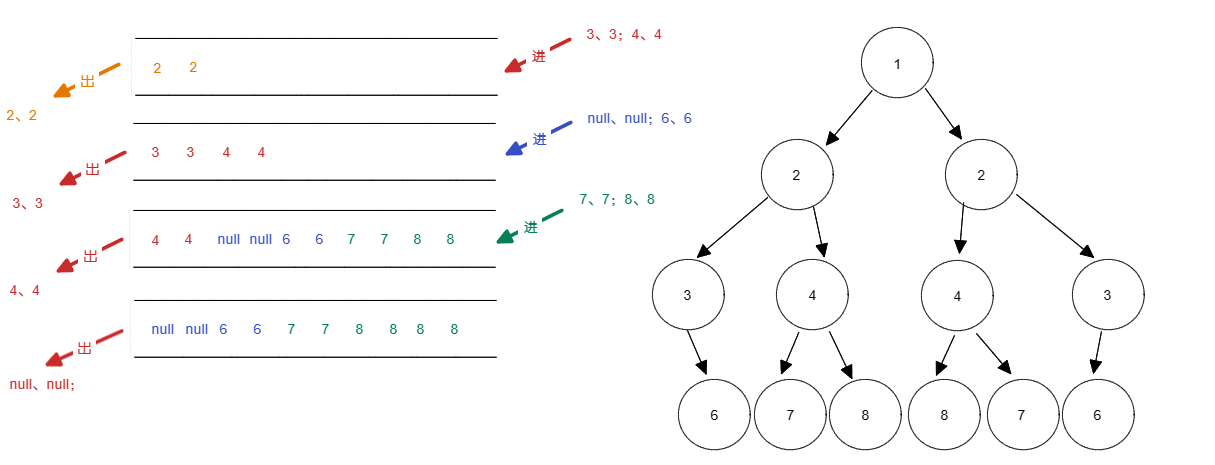
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
queue<TreeNode*> que;
que.push(root->left); // 将左子树头结点加入队列
que.push(root->right); // 将右子树头结点加入队列
while (!que.empty()) { // 接下来就要判断这两个树是否相互翻转
TreeNode* leftNode = que.front(); que.pop();
TreeNode* rightNode = que.front(); que.pop();
if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的
continue;
}
// 左右一个节点不为空,或者都不为空但数值不相同,返回false
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
que.push(leftNode->left); // 加入左节点左孩子
que.push(rightNode->right); // 加入右节点右孩子
que.push(leftNode->right); // 加入左节点右孩子
que.push(rightNode->left); // 加入右节点左孩子
}
return true;
}
};